
scherbo-sp2
.pdf
Однако в данном случае можно получить решение, считая, что на участке dt стержня (рис. 12.19) приложен сосредоточенный элементарный момент
dMt = mt dt. |
(12.71) |
Рис. 12.19
Тогда влияние этого момента на угол Θn можно определить из выра- жения
|
|
|
|
m dt |
|
|
|
shk (z − t) |
|
|
|
|
|||||||
Θn(m) |
= |
|
t |
|
(z − t) − |
|
|
|
. |
|
|
|
(12.72) |
||||||
|
|
|
|
|
k |
|
|
|
|||||||||||
|
|
|
|
GJd |
|
|
|
|
|
|
|
|
|
||||||
Влияние всех распределенных моментов можно найти как интеграл: |
|
||||||||||||||||||
|
|
|
z |
|
m |
|
|
|
|
|
|
|
shk (z − t) |
|
|
|
|
||
Θn(m) = ∫ |
|
t |
|
|
(z |
− t) − |
|
|
|
dt. |
|
|
(12.73) |
||||||
|
|
|
|
|
k |
|
|
|
|||||||||||
|
|
a |
|
GJd |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для случая, когда mt = m = const, получим |
|
|
|
|
|
|
|
|
|||||||||||
Θn(m) = |
m (z − a )2 |
− |
1 |
|
chk (z − ai ) + |
1 |
|
||||||||||||
|
|
|
|
|
|
i |
|
|
|
|
. |
(12.74) |
|||||||
|
|
|
2 |
k 2 |
k |
2 |
|||||||||||||
|
GJd |
|
|
|
|
|
|
|
|
||||||||||
Таким образом, при наличии распределенных моментов к уравнению (12.70) добавляется правая часть уравнения (12.73) или (12.74).
Путем последовательного дифференцирования (12.70) с учетом (12.73) или (12.74), а также полученных ранее уравнений (12.40) и (12.45) могут быть составлены общие уравнения Θ, Вω и Мω для любого участка стержня.
Вэти уравнения войдут неизвестные начальные параметры, которые
вкаждой задаче определяются исходя из граничных условий.
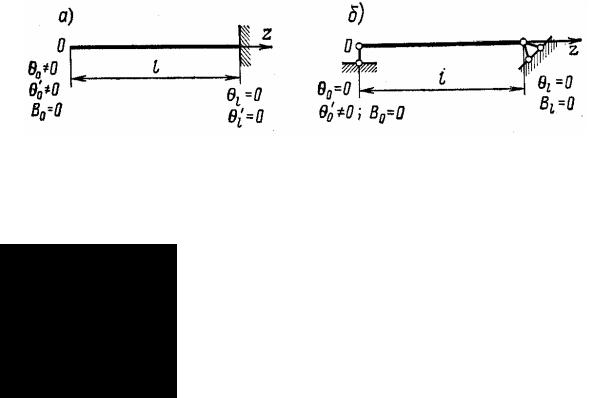
Так, например, если один конец стержня свободен, а другой жестко заделан (рис. 12.20, а), то известными граничными условиями будут:
1) угол закручивания на заделанном конце стержня Θl = 0 , так как сечение в заделке не может поворачиваться;
2) производная Θ′ = 0 . Это следует из полученного в п. 12.4 равенст-
l
ва ∂u = −rΘ′, так как для сечения в заделке перемещения u = 0 , а расстоя-
∂s
ние r в общем случае не равно нулю;
121
3)на свободном конце стержня В0 = 0. Это равенство вытекает из формулы (12.43) ввиду того, что в торцовом сечении стержня σω = 0;
4)Mко известен как внешний сосредоточенный момент. Неизвестные
начальные параметры Θ0 и Θ′ определяются в данном случае путем под-
0
становки первого и второго граничных условий в соответствующие урав- нения для Θ и Θ'.
Рис. 12.20
Для другого случая, когда стержень шарнирно оперт по концам (рис. 12.20, б), можно считать, что опорные сечения не могут поворачи- ваться в плоскости хoу, так как такому повороту препятствуют элементы, прикрепленные к опорам (рис. 12.21). Поэтому угол Θ0 = 0, а также и на дру- гой опоре Θl = 0 ; равны нулю и бимоменты в обоих
торцовых сечениях стержня, так как здесь σω = 0.
Неизвестные начальные параметры Θ′ и Мко
0
для рассматриваемого стержня определятся в ре- зультате решения двух уравнений:
Рис. 12.21 |
Θl |
= 0 |
и Bl = 0. |
|
Следует заметить, что для случая, когда влиянием жесткости стержня при чистом кручении можно пренебречь, т. е. положить
GJd = 0, |
(а) |
уравнение (12.54) запишется в таком виде: |
|
EJ ΘIV = m. |
(б) |
ω |
|
Это уравнение по своей форме совпадает с известным из теории из- гиба уравнением
EJvIV = q. |
(в) |
Из аналогии (б) и (в) можно установить зависимости при стесненном кручении и поперечном изгибе.
122
Стесненное |
Поперечный |
кручение |
изгиб |
EJ QIV = m |
EJvIV = q |
ω |
EJv¢¢¢ = Q |
EJωQ¢¢¢ = M ω |
|
EJωQ¢¢ = Bω |
EJv¢¢ = Mu |
EJωQ¢ |
EJv¢ |
EJωQ |
EJv |
12.8.Вычисление геометрических характеристик
12.8.1.Определение положения центра изгиба А
Как было показано ранее, сечение стержня при кручении поворачи- вается, как жесткий диск, вокруг некоторого полюса в точке А, которую называют также центром кручения. При этом внешняя поперечная сила, например, сила Р (рис. 12.22), тем больше будет закручивать стержень, чем больший момент она создает относительно точки А.
Если сила Р проходит через точку А, то закручивающий момент равен нулю, а следовательно, поворота сечений не про- изойдет и стержень будет испытывать только один изгиб.
Рис. 12.22 Поэтому полюс А, или центр круче- ния, является также и центром изгиба.
Для определения координат центра изгиба используем равенства (12.6), из которых получим
∫ sω ydF = 0 и ∫sωxdF = 0. |
(a) |
||
F |
|
||
Первое из равенств (а) после подстановки в него значений (12.47) |
|||
для sω запишется так: |
|
||
|
Bω |
∫ wydF = 0. |
(12.75) |
|
|
||
|
Jω F |
|
|
Интеграл в левой части называется секториально-линейным статиче- ским моментом сечения относительно оси Ох и обозначается через Sωх.
Эта новая геометрическая характеристика сечения измеряется в сан-
тиметрах в пятой степени (см5). Учитывая, что |
Bω |
¹ 0, |
получим |
|
|||
|
Jω |
|
|
Sωx = ∫ wydF = 0. |
(12.76) |
||
F |
|
||
123

Второе равенство после аналогичной подстановки соответственно дает
Sωy = ∫ωxdF = 0. |
(12.77) |
Sωy называют также секториально-линейным статическим моментом се- чения относительно оси oу.
Равенства (12.76) и (12.77) и будут теми условиями, которые позво- лят определить координаты сектори- ального полюса (или центра изгиба).
Рассмотрим какое-либо сечение (рис. 12.23), главные центральные оси которого совместим с осями oу и oх. Подобно тому как при отыскании центра тяжести берется произволь- ная ось и от нее определяется рас- стояние до центральной оси, выбе- рем произвольный полюс В и поло- жение центра изгиба будем опреде- лять относительно указанного полю- са отрезками αх и αy.
Наметим на профиле сечения любую точку m и проведем к ней ка- сательную, угол наклона которой к вертикали обозначим через β. Элемен-
тарная секториальная площадь, определяющая секториальную координату точки m при полюсе В, равна
|
|
|
dωB = dsrB , |
(12.78) |
||
а при полюсе А |
dωA = dsrA. |
|
||||
|
|
|
(12.79) |
|||
Разность этих площадей можно выразить следующим образом: |
||||||
dωB − dωA = dsrB − dsrA = ds r, |
(12.80) |
|||||
или, выражая r через отрезки αх и αy согласно рис. 12.23 получим |
|
|||||
dωB − dωA = ds(αx cosβ + α y sin β). |
(б) |
|||||
Учитывая далее, что |
|
|
|
|
||
cosβ = |
dy |
|
и sin β = − |
dx |
, |
(в) |
ds |
|
|||||
|
|
ds |
|
|||
получим после сокращения на ds |
|
|
|
|
||
dωB − dωA = αxdy − α ydx. |
(12.81) |
|||||
Интегрируя полученное равенство и добавляя произвольную постоянную С, имеем
ωB − ωA = αx y − α y x + C, |
(12.82) |
124
откуда |
ωA = ωB − αx y + α y x − C. |
|
|
||||||||
|
|
(12.83) |
|||||||||
Подставим в выражение (12.76) значение секториальной площади из |
|||||||||||
уравнения (12.83), соответствующей искомому полюсу А: |
|
||||||||||
∫ ωA ydF = ∫ (ωB − αx y + α y x − C ) ydF = ∫ ωB ydF − αx ∫ y2dF + |
|||||||||||
F |
F |
|
|
|
|
|
|
|
F |
F |
|
|
+ α y ∫ xydF − C ∫ ydF = 0, |
|
|
||||||||
|
F |
|
F |
|
|
|
|
|
|
|
|
или |
∫ ωA ydF = SωB x − αx J x + α y J xy − CSx = 0. |
|
|||||||||
|
(12.84) |
||||||||||
|
F |
|
|
|
|
|
|
|
|
|
|
В связи с тем, что оси oу и oх являются, по условию, главными цен- |
|||||||||||
тральными осями инерции, J xy = 0 |
и Sx = 0 , следовательно, |
|
|||||||||
|
α |
x |
= |
Sω |
B |
x |
. |
|
|
(12.85) |
|
|
|
J x |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
При подстановке того же значения ωА в условие (12.77) получим |
|||||||||||
|
∫ ωAxdF = SωB y − αx J xy + α y J y − CS y = 0. |
(12.86) |
|||||||||
|
F |
|
|
|
|
|
|
|
|
|
|
Здесь также Jxy = 0 и Sy = 0. Следовательно, |
|
|
|
|
|||||||
|
α y |
= − |
Sω |
B |
y |
. |
|
(12.87) |
|||
|
J y |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||
В формулах (12.85) и (12.87) величины SωB x |
и SωB y |
представляют |
|||||||||
собой секториально-линейные статические моменты сечения, определяе- мые при расположении полюса в произвольной точке В, поэтому эти фор- мулы определяют положение центра изгиба А относительно точки В. При этом следует иметь в виду, что координаты αх и αу откладываются от по- люса В с учетом их знаков, а именно: если они положительны, то их от- кладывают в положительном направлении осей oу и oх.
12.8.2.Определение главной секториальной нулевой точки М0
Вп. 12.5 было установлено, что положение точки M0, являющейся
началом отсчета ω, связано с удовлетворением условия (12.25)
Sω = ∫ ωdF = 0.
F
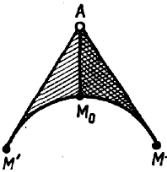
Возьмем за начало отсчета произвольную точку М' и, используя ука- занное условие, определим главную нулевую точку М0 (рис. 12.24).
125
|
Если обозначить через w' секториальную |
||||||
|
площадь для текущей точки М при начале отсчета |
||||||
|
в М', а через w – |
секториальную площадь той же |
|||||
|
точки М при начале отсчета в М0, то, очевидно, |
||||||
|
имеет место следующее равенство: |
|
|||||
|
|
|
|
|
′ |
(12.88) |
|
|
|
|
|
ω = ω − D, |
|||
|
где D – |
постоянная величина, равная удвоенной |
|||||
Рис. 12.24 |
площади сектора AM'M0. |
|
|||||
Подставляя теперь значение (12.88) для w в |
|||||||
|
|||||||
|
(12.25), получим |
|
|
|
|||
|
∫ wdF = ∫ (w¢ - D) dF = 0, |
(а) |
|||||
|
F |
F |
|
|
|
||
или |
|
|
|
|
|
|
|
|
∫ w¢dF - D ∫ dF = 0, |
(б) |
|||||
|
F |
|
F |
|
|
|
|
откуда найдем |
|
|
∫ w¢dF |
|
|||
|
|
|
|
||||
|
|
D = |
F |
|
. |
(12.89) |
|
|
|
F |
|
||||
|
|
|
|
|
|
||
Таким образом, для определения положения точки М0 следует вначале построить эпюру w', взяв произвольную точку начала отсчета, затем необхо- димо вычислить по формуле (12.89) постоянную D и, пользуясь равенством (12.88), построить эпюру w, которая и будет удовлетворять условию (12.25). Для некоторых типов сечений на эпюре w будет несколько нулевых точек. Это означает, что при депланацин все эти точки не имеют продольных сме- щений. Любая из них может быть принята за точку начала отсчета. Однако за главную нулевую точку принимают ближайшую к полюсу А.
12.8.3. Техника вычисления геометрических характеристик Пример. Для равнополочного несимметричного двутавра, показан-
ного на рис. 12.25, определить координаты центра изгиба, главную нуле- вую точку отсчетов w и вычислить секториальный момент инерции.
По эпюрам Y и X (рис. 12.26, а, б) вычисляем главные центральные моменты инерции, пользуясь формулой Верещагина:
J y = ∫ x2dF = 2 ×1× 24 ×1 + |
2 ×1×15 |
[2(6 ×6 + 9 ×9 - 6 ×9)] = 678см4 ; |
|||||||
|
|
||||||||
|
F |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J x |
= ∫ |
y2dF = 2 ×1×12 ×15 ×12 |
+ |
2 × 2 ×12 ×12 |
× |
2 |
×12 = 6624 см4. |
||
|
|
||||||||
|
F |
|
|
2 |
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
126
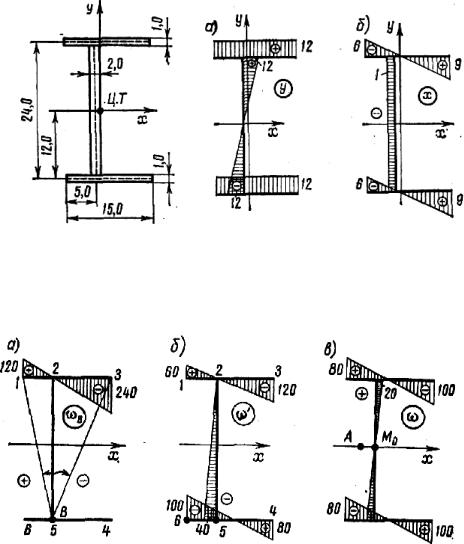
Рис. 12.25 Рис. 12.26
Строим эпюру wB, располагая полюс В в точке 5 и начало отсчетов wB в точке 2 (рис. 12.27, а).
Рис. 12.27
Перемножая эту эпюру последовательно с эпюрами X и Y, получаем секториально-линейные статические моменты:
SωB y |
= |
1×15 |
[-2 ×6 ×120 - 2 ×9 × 240 + 6 × 240 + 9 ×120] = -8100 cм5; |
|||||
|
||||||||
|
6 |
|
|
1×120 ×5 |
|
1× 240 ×10 |
|
|
|
|
SωB x |
= |
×12 |
×12 = -10800 см5. |
|||
|
|
|
|
|||||
|
|
|
|
2 |
2 |
|
||
По формулам (12.85) и (12.87) вычисляем координаты центра изгиба:
ay = - |
Sω |
B |
y |
= - |
-8100 |
=12 |
см; |
|||||||||
|
J y |
|
678 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
ax |
= - |
Sω |
B |
x |
|
= - |
10800 |
|
= -1,63 см. |
|||||||
|
J x |
|
|
|
|
6624 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Центр изгиба, как и надо было ожидать, располагается на оси ох, яв- ляющейся осью симметрии.
127

Для определения главной нулевой точки строим эпюру w', распола- гая полюс в центре изгиба и беря за начало отсчетов произвольную точку, а именно точку 2 (см. рис. 12.27, б).
Используя эпюру w¢, по формуле (12.89) вычисляем постоянную D, применяя способ Верещагина:
|
∫ w¢dF |
|
|
|
|
|
|
|
|
|
|||
D = |
F |
|
= |
-120 + 60 |
15 ×1- |
1 |
× 40 × 24 × 2 + |
||||||
|
|
|
|
|
|||||||||
|
F |
|
|
2 |
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
-100 + 80 |
|
|
1 |
|
|
|
2 |
|
|||
|
+ |
2 |
|
15 |
×1 |
|
|
= -20 см |
|
. |
|||
|
|
|
|
|
|||||||||
|
|
|
|
76 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
Для построения эпюры w находим по равенству w = w - D : |
|||||||||||||
w = 60 - (-20) = 80 см2 ; |
|
|
|
|
ω2 = 0 − (−20) = 20 см2; |
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
w = -120 - (-20) = -100 см2 ; |
|
|
|
ω4 = 80 − (−20) = 100 см2 ; |
|||||||||
3 |
|
|
|
|
|
|
|
|
ω6 = −100 − (−20) = −80 см2. |
||||
w = -40 - (-20) = -20 см2 ; |
|
|
|
|
|||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
По этим данным на рис. 12.27, в построена эпюра ω. Искомой нуле- вой точкой будет ближайшая к центру изгиба, т. е. М0.
Секториальный момент инерции найдем, умножив эпюру ω саму на
себя. В результате получим |
|
|
|||||
J |
ω |
= d |
∫ |
w2ds = 2 |
1×15 |
2 |
(80 ×80 +100 ×100 - 80 ×100) + |
|
|||||||
|
|
6 |
|
|
|||
|
|
|
F |
|
|
|
|
+ 2 × 2 × 20 ×12 × 2 ×90 = 90400 см6.
23
12.9.Общий случай действия сил на тонкостенный стержень
На практике тонкостенные стержни подвергаются воздействию раз- личных внешних нагрузок, вызывающих помимо закручивания другие ви- ды деформации.
В общем случае сложного сопротивления задача решается на основе принципа независимости действия сил путем суммирования результатов, получаемых отдельно для каждого вида деформации.
Формула нормальных напряжений запишется следующим образом:
|
N |
|
M |
x |
|
M y |
|
B |
|
|
s = |
|
+ |
|
y + |
|
x + |
ω |
w. |
(12.90) |
|
|
|
|
J y |
|
||||||
|
F |
|
J x |
|
Jω |
|
||||
Первые три слагаемых в правой части этой формулы учитывают на- пряжения, зависящие от продольной силы и изгибающих моментов. Чет- вертое слагаемое определяет нормальные напряжения от бимомента.
128
Полное касательное напряжение в исследуемой точке определяется
алгебраической суммой касательных напряжений: |
|
τ = τ1 + τ2 + τω + τ0 , |
(12.91) |
где tω и t0 – напряжения, возникающие при стесненном кручении и опре- деляемые по формулам (12.42) и (12.1); t, и t2 – напряжения при попереч- ном изгибе, зависящие от составляющих поперечной силы Qy и QX. Эти на- пряжения определяются по формулам, аналогичным формуле Журавского:
|
|
|
отс |
|
|
|
t = |
Qy Sx |
|
; |
|
||
|
|
|
||||
1 |
|
J xd |
|
|
|
|
|
|
|
(12.92) |
|||
|
|
Q S |
отс |
|
|
|
|
|
|
|
|
||
t2 = |
|
x |
y |
|
. |
|
|
J yd |
|
|
|||
|
|
|
|
|
||
Однако в отличие от нетонкостенных стержней при вычислении Sxотс
часть сечения, расположенная по одну сторону от исследуемой
точки, отсекается плоскостью, не перпендикулярной одной из главных осей oу или oх, а перпендикулярной линии контура сечения, т. е. так, как на рис. 12.14 при выводе формулы tω (12.32).
Напряжения t1 и t2 в рассматриваемом случае не будут параллельны осям oу или oх, как это имело место не в тонкостенном стержне. Эти на- пряжения будут направлены вдоль средней линии каждого элемента сече-
ния (см. рис. 12.14).
Ниже дается пример определения напряжений в тонкостенном стержне, работающем одновременно в условиях стесненного кручения и поперечного изгиба.
Пример. Определить наибольшие нормальные и касательные на- пряжения в сечении стержня у заделки (рис. 12.28, а), если известно, что в
указанном сечении бимомент Bω =17278805 кгс×см2 , изгибно-крутящий момент Mω = 77800 кгс×см, момент чистого кручения М0 = 0; изгибающий момент M x = 800000 кгс×сми поперечная сила Qy = 2000 кгс.
Решение. С учетом заданных размеров сечения и положения центра изгиба А (рис. 12.28, б) построена эпюра главных секториальных коорди- нат w (рис. 12.29) и вычислен секториальный момент инерции Jω = 7024644 см6. По соответствующей эпюре ординат у вычислен момент инерции J x = 82944 см4.
Определение нормальных напряжений. В сечениях стержня, кроме нормальных напряжений sω, связанных со стесненным кручением, возни- кают также и напряжения sИ, связанные с поперечным изгибом стержня относительно оси Ох. В заданном сечении указанные напряжения дости- гают наибольшей величины.
129
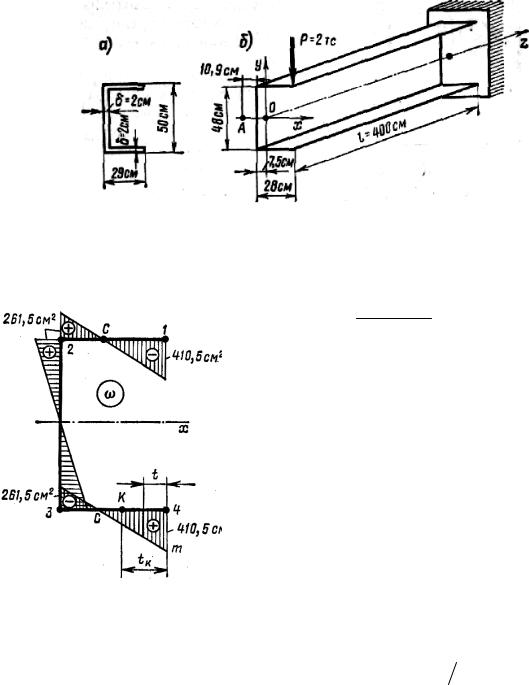
Рис. 12.28
Определим вначале sω. Для этого в формулу (12.47) подставим чи- словые значения Вω и Jω
sω = 17278805 w = 2, 4597w. 7024644
По формуле (а) на рис. 12.30, а по- строена эпюра sω, при этом значения секто- риальных координат взяты с эпюры w, дан- ной на рис. 12.29.
Как видно, знаки на эпюрах w и sω сов- падают, причем плюс соответствует растяги- вающим напряжениям, а минус – сжимающим, что также легко установить, если рассмотреть общую картину деформации стержня при стес- ненном кручении.
Наибольшее значение напряжений sИ в
Рис. 12.29
крайних волокнах полок определится по из-
вестной формуле |
|
|
|
|
|
|
sИ |
= ± |
M x |
ymax |
= ± |
2000 × 400 |
× 25 = 241кгс см2. |
|
|
|||||
|
|
J x |
82944 |
|
||
На рис. 12.30, б представлена эпюра напряжений sИ, а на рис. 12.30, в – суммарная эпюра нормальных напряжений σω + σИ .
Определение касательных напряжений. Из двух систем касательных напряжений, соответствующих стесненному кручению, в заданном сече- нии возникают лишь напряжения tω, так как момент чистого кручения в указанном сечении равен нулю.
Кроме tω, в стержне развиваются касательные напряжения, соответ- ствующие поперечному изгибу.
130
