scherbo-sp2

1. Составить уравнения прогибов и углов поворота, а также опреде- лить, место положения и величину наибольшего прогиба в балке, изо- браженной на рис. 8.11.

Рис. 8.11

В данной балке всего один участок, так на всем протяжении балки нет никаких изменений в нагрузке. По универсальному уравнению (8.10) с учетом того, что v0 = 0, Q0 = M 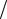l, имеем

Для определения неизвестной величины угла поворота используем граничное условие: при z = l v = 0.

Таким образом,

откуда находим

ϕ0 = − Ml . 6EJ

Следовательно, уравнение прогибов имеет вид

Дифференцируя, получим уравнение углов поворота

dv = ϕ = − Ml + M z2 . dz 6EJ l 2EJ

Для того чтобы определить расстояние до места наибольшего проги- ба z0, воспользуемся условием

21

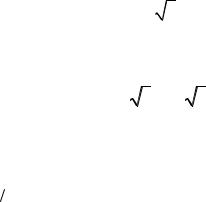
откуда

Подставляя найденное значение z0 в уравнение (з), получим

Интересно отметить, что этот прогиб очень мало отличается от про- гиба в середине пролета:

8.5.Метод Мора для определения перемещений

Впредыдущих параграфах настоящей главы определялись переме- щения в балках с прямой осью. Для брусьев с ломаной осью и для систе- мы, состоящей из нескольких стержней, применение описанных выше ме- тодов вызывает затруднения. Более универсальным является метод Мора, который широко применяется в теории расчета стержневых систем. Этот метод основан на известном из теоретической механики принципе воз- можных перемещений.

Для удобства применения этого метода условимся относительно обо- значений. Перемещение какой-либо точки по определенному направлению

от какой-либо силы или группы сил обозначается греческой буквой , а перемещение от силы, равной единице, – буквой δ. Кроме того, каждое из перемещений обозначается двумя значками, например, КР, Kt , δmn и т. п.

Первый значок обозначает точку, для которой определяется перемещение и вместе с тем направление этого перемещения, а второй значок опреде- ляет причину, вызвавшую данное перемещение.

Так, например, КР может обозначать перемещение точки К и верти- кали от группы сил Р. Если в какой-либо точке приложена сила PK по опре- деленному направлению, то величину КР можно рассматривать как пере- мещение по направлению силы РK от нагрузки, обозначаемой индексом Р.

Перемещение по направлению силы РK от температурного возму- щения соответственно следует обозначать Kt . Второй значок t показыва-

ет, что причиной, вызвавшей перемещение, является температура.

Под обозначением δmn нужно понимать перемещение по направле- нию воздействия m от n-й единичной силы. Если перемещение берется по направлению момента, то оно представляет собой угол поворота.

22

Такие обозначения обладают универсальностью, их можно понимать в обобщенном смысле не только как линейное или угловое, но и как груп- повое перемещение, например сближение каких-либо двух точек и т. п.

В теоретической механике начало возможных перемещений приме- няется к абсолютно жестким телам. По этому принципу в положении рав- новесия работа всех сил на любых бесконечно малых возможных допус- каемых связями перемещениях равна нулю:

где Kn – составляющая возможного перемещения точки приложения силы РК по направлению этой силы от n-го возможного перемещения системы.

Уравнение (8.13) применяется для исследования равновесия твердых тел, в частности для определения опорных реакций.

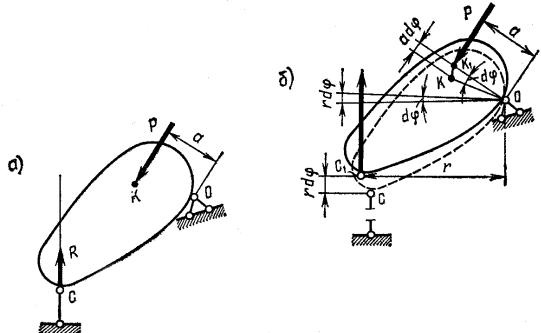
Для примера рассмотрим жесткий диск, показанный на рис. 8.12, а.

Рис. 8.12

Поставим задачу определить опорную реакцию R. Разрежем опорный стержень и сообщим диску возможное бесконечно малое перемещение. При этом диск повернется вокруг точки О на бесконечно малый угол dϕ. Точка K приложения силы Р переместится в точку К1, а точка приложения реакции R переместится в точку С1 (рис. 8.12, б).

Перемещения точек приложения сил Р и R по направлению их дейст- вия от этого угла поворота составят:

Rϕ = rdϕ, Pϕ = adϕ.

23

Составляя уравнение принципа возможных перемещений, имеем

R Rϕ − P Pϕ = 0.

Знак минус перед последним членом поставлен потому, что пере- мещение Pϕ направлено в сторону, противоположную направлению дей-

ствия силы Р.

Решая полученное уравнение относительно R, найдем

Точно такой же результат получится, если использовать обычное ypaвнение равновесия в виде

∑m0 = 0.

Рассмотрим теперь не абсолютно жесткое, а деформируемое упругое тело. Если задать точкам такого тела, находящегося в равновесии, беско- нечно малые перемещения, при которых появляются деформации, то в те- ле возникнут внутренние силы, которые также произведут работу.

В этом случае уравнение принципа возможных перемещений (8.13) запишется так:

Здесь первое слагаемое, так же как и в уравнении (8.13), представля- ет собой работу внешних сил на заданных возможных перемещениях, а второе слагаемое – работу внутренних сил также на возможных переме- щениях внутренних частиц тела.

Предположим, что при возможных перемещениях величина и на- правление всех внешних и внутренних сил остаются неизменными, такими же, как в исходном состоянии, т. е., как обычно, ввиду малости перемеще- ний здесь не учитывается перераспределение усилий, связанное с дефор- мацией тела.

Следовательно, в качестве возможных можно брать и конечные, но малые перемещения, например, определяемые на основе гипотез сопро- тивления материалов прогибы и углы поворота от какой-либо конкретной нагрузки.

Рассмотрим ломаный брус, показанный на рис. 8.13, а, под действи- ем силы РК = 1. В качестве возможных перемещений примем перемеще- ния, которые произойдут вследствие деформации одного малого элемента длиной ds, расположенного в пределах, например, вертикальной стойки (рис. 8.13, а). Предположим, что деформация элемента ds произошла от какой-либо группы сил. При обозначении внутренних сил и перемещений от этой нагрузки будем применят индекс Р. Так, например, внутренние си- лы в элементе ds от этой группы сил будут NP, МР и QP. Перемещение по направлению силы PK = 1 (рис. 8.13, б) обозначим d KP . Оно равно про-

24

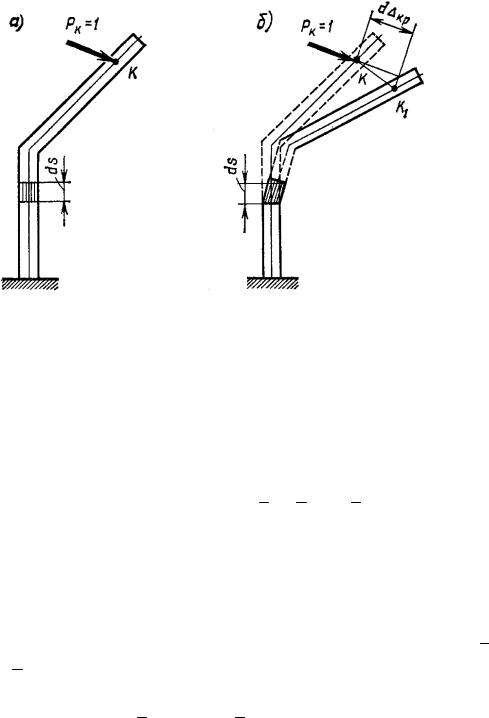
екции полного перемещения точки K (отрезок KK1) на направление дейст- вия силы PK =1.

Рис. 8.13

Пользуясь формулой (8.14) для рассматриваемого случая, имеем

званных силой PK = 1 на перемещениях ( ds)P, dϕP и сдвигах γР, которые возникли вследствие деформации одного элемента ds. Эта деформация произошла от некоторой группы сил Р (на рис. 8.13 они показаны). Чер-

точка, проведенная над обозначениями NK , M K и QK , показывает, что соответствующие значения найдены от единичной силы.

Общую деформацию элемента ds можно представить в виде трех составляющих: удлинения dsР (рис. 8.14, а), угла поворота сечения dϕP (рис. 8.14, б) и сдвигов каждого из волокон γP (рис. 8.14, в).

Внутренние силы, возникающие в элементе ds от силы PK = 1, яв-

ляются по отношению к нему внешними силами. Нормальная сила NK :

и момент M K на перемещениях ( ds)P и dϕP совершают работу, равную

(рис. 8.14)

NK ( ds)P + M K dϕP . (a)

Касательные напряжения распределены в сечении по сложному за- кону. Для определения работы сил τКdF на перемещениях γРds составим уравнение

25

Рис. 8.14

Складывая выражения (а) и (б), получим работу сил NK и M K и усилий, вызывающих сдвиги в элементе ds. Поскольку эти силы по отно- шению к элементу ds являются внешними, то работа внутренних сил будет иметь обратный знак. В силу сказанного второе слагаемое, входящее в формулу (8.15), определяется равенством

Эта величина является безразмерной и для каждого сечения может быть вычислена по формуле (8.17).

Подстановка дает

26

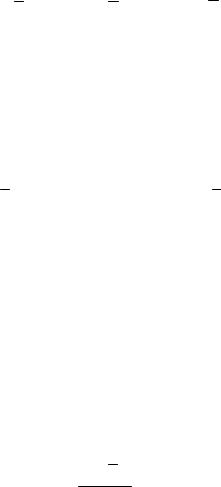
после подстановки этих выражений и выражения (8.18) в формулу (8.16) получим

Это перемещение возникает вследствие деформации только одного малого элемента ds. Для учета деформаций всей системы в целом необхо- димо проинтегрировать (8.19), распространяя интегрирование на все эле- менты системы. Принято такой интеграл снабжать индексом «s» внизу, ко- торый символизирует учет деформации всей системы в целом. Таким обра- зом, имеем формулу Мора

Необходимо иметь в виду, что входящие в формулу Мора силовые факторы берутся в произвольной точке и поэтому представляют собой аналитические функции от координат произвольных точек.

Для шарнирно-стержневых систем, в которых стержни работают только на осевую силу, в формуле Мора (8.20) отличен от нуля только первый интеграл. В этом случае нормальная сила по длине каждого стержня обычно не меняет своей величины, поэтому подынтегральное выражение как постоянная величина выйдет за знак интеграла, а сам ин- теграл превратится в длину стержня. Учитывая деформацию всех стерж- ней, получим

KP = ∑ NP NK l.

EF

Так как рассматриваются только плоские стержневые системы, то знач- ки у М, N, Q и I опускаем, т. е. считается, что M x = M , Qy = Q, I x = I и т. п.

Остановимся теперь на технике вычисления интегралов Мора. Заметим, что все три интеграла формулы Мора (8.20) имеют одина-

ковый вид, который в общем виде можно представить так:

Предположим, что одна из подынтегральных функций является ли- нейной функцией, а вторая, например, f(s) – произвольной. На рис 8.15 показан примерный вид функций f(s) и ϕ(s).

Из рис. 8.15 видно, что

ϕ(s) = s tgα, f (s)ds = dΩ.

Подставляя эти выражения в интеграл (8.21), получим

= tgα∫sdΩ.

27

Пример 1

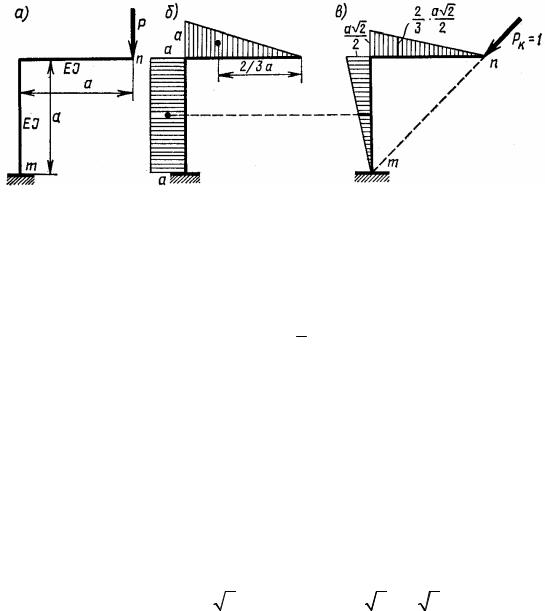
Определить, на сколько изменится расстояние между точками m и n в результате деформации от изгиба рамы, показанной на рис. 8.17, а, под действием силы P = 1.

Рис. 8.17

Жесткости обоих стержней одинаковые и равны EJ. При определе- нии перемещений в рамах обычно пренебрегают влиянием нормальных и поперечных сил и формулой Мора (8.20) учитывают только один интеграл, определяющий изгибные деформации:

29

М-9. ПРОСТЕЙШИЕ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ И БАЛКИ, ЛЕЖАЩИЕ НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ

9.0. Введение в модуль

Модуль содержит следующие структурные элементы:

1.Статически неопределимые балки при изгибе.

2.Канонические уравнения метода сил.

3.Расчет простейших статически неопределимых стержневых систем по методу сил.

4.Расчет статически неопределимых балок по методу разрушающих нагрузок.

5.Дифференциальное уравнение оси изогнутой балки, лежащей на сплошном упругом основании.

6.Расчет бесконечно длинной балки, лежащей на сплошном упругом основании, при действии на нее одной сосредоточенной силы Р.

7.Понятие о расчете коротких балок, лежащих на сплошном упругом основании. Метод начальных параметров.

Цель модуля – изучить расчет статически неопределимых систем методом сил.

9.1. Статически неопределимые балки при изгибе

Изложенные в предыдущей главе методы определения перемещений широко применяют в расчетах так называемых статически неопределимых балок. Более подробно расчет сложных статически неопределимых систем излагается в курсе «Статика сооружений». В настоящей главе рассмотрим метод расчета простейших статически неопределимых стержневых систем.

Балка, способная воспринять произвольную нагрузку, должна быть закреплена таким образом, чтобы она не могла перемещаться как жесткое тело. В случае действия нагрузки в одной плоскости минимальное количе- ство связей, необходимых для закрепления балки, равно трем.

Эти три связи являются абсолютно необходимыми. Удаление хотя бы одной из таких связей превращает балку в геометрически изменяемую систему (механизм), т. е. в такую систему, в которой могут происходить перемещения точек без деформации стержней.

Поскольку для плоской системы сил можно составить три уравнения равновесия, реакции абсолютно необходимых связей могут быть найдены с помощью лишь одних уравнений статики.

Балка, закрепленная такими связями, является статически опреде-

лимой.

30