scherbo-sp2

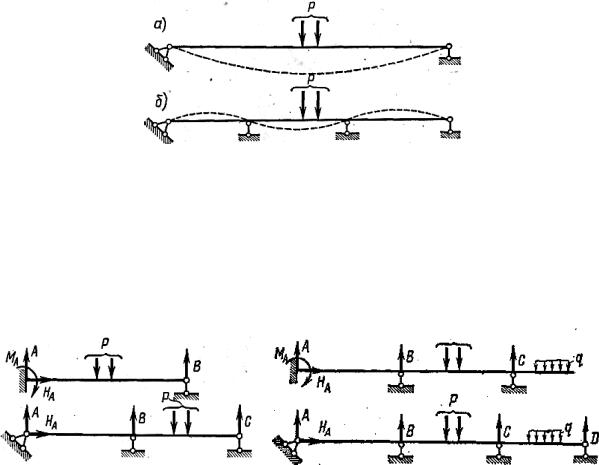
На практике встречаются балки, в которых число наложенных связей больше, чем нужно для обеспечения геометрической неизменяемости. В этом смысле некоторые связи являются лишними. В балках с лишними связями все реакции нельзя определить только из уравнений равновесия.

Такие балки будут статически неопределимыми.

Заметим, что термин «лишние связи» нужно понимать условно. В действительности же по условиям работы конструкции эти связи являют- ся необходимыми, так как при их отсутствии прочность и жесткость сис- темы могут оказаться необеспеченными. Из рис. 9.1 видно, что при одной и той же нагрузке прогибы в статически неопределимой балке (рис. 9.1, б) будут значительно меньше, чем в статически определимой балке такой же длины (рис. 9.1, а). Таким образом, добавленные закрепления сделали конструкцию более жесткой.

В статически неопределимых балках число неизвестных опорных ре- акций всегда превышает число возможных уравнений равновесия. Некото- рые реакции являются как бы добавочными, «лишними». В дальнейшем их будем называть лишними неизвестными.

Рис. 9.1

Число лишних неизвестных определяет степень статической неопре- делимости системы. На рис. 9.2 показаны балки, у которых четыре опор- ные реакции, а независимых уравнений статики три, поэтому балки будут один раз статически неопределимыми. На рис. 9.3 представлены дважды статически неопределимые балки.

P

31

Метод расчета статически неопределимых изгибаемых балок по су- ществу не отличается от рассмотренных ранее методов решения статиче- ски неопределимых задач на растяжение и кручение.

Вначале отбрасывают лишние связи, заменяя их действие лишними неизвестными, тем самым превращают заданную балку в статически опре- делимую. Полученная балка называется основной системой.

Для определения лишних неизвестных Х1, Х2, ..., Хn составляют усло- вия деформации системы, смысл которых заключается в том, что основная система под действием приложенной нагрузки и лишних неизвестных де- формируется так же, как и заданная статически неопределимая балка, т. е. эти уравнения выражают условия о том, что перемещения в основной сис- теме должны соответствовать тем ограничениям, которые накладываются на систему с отброшенными связями. В дальнейшем эти уравнения будем называть уравнениями совместности деформаций или для краткости про- сто уравнениями деформаций.

После вычисления лишних неизвестных из уравнений равновесия находим остальные опорные реакции и строим эпюры внутренних сило- вых факторов.

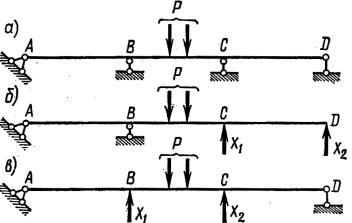
Для одной и той же балки (рис. 9.4, а) основная система может быть выбрана по-разному (рис. 9.4, б, в), при этом уравнения деформаций будут иметь различный смысл. Например, для основной системы, показанной на рис. 9.4, б, уравнения деформаций имеют вид

vC = 0 и vD = 0 .

Эти уравнения получены из условия, что суммарные прогибы в точ- ках С и D от действия неизвестных сил Х1 и Х2 и от внешней нагрузки Р равны нулю, так как в действительности эти точки в заданной системе по вертикали не смещаются.

Рис. 9.4

В некоторых задачах при выборе основной системы удобно отбра- сывать не внешние, а внутренние связи, например, разрезать балку и вве-

32

сти шарнир (рис. 9.5). Здесь лишним неизвестным является изгибающий момент М.

Рис. 9.5

Смысл уравнения деформации в этом случае – отрицание угла поворо- та сечения у заделки от действия силы Р и неизвестного момента М: ϕВ = 0.

Выбирая основную систему, во всех случаях нужно следить за тем, чтобы она была статически определимой и геометрически неизменяемой.

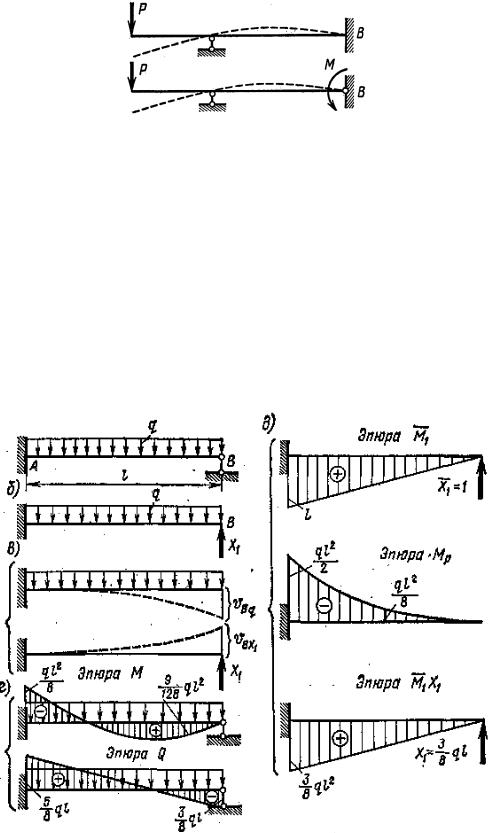
Рассмотрим порядок расчета простейших статически неопределимых балок на следующем примере. На рис. 9.6, а показана один раз статически неопределимая балка. Один из возможных вариантов основной системы для этой балки представлен на рис. 9.6, б. По этому варианту правая шар- нирно-подвижная опора заменяется неизвестным усилием Х1.

Условием деформации основной системы является требование ис- ключить вертикальное перемещение (прогиб) в точке В.

а)

Рис. 9.6

33

Выражение для прогиба vВ может быть представлено в виде

Из уравнения (9.1) видно, что прогиб конца консоли от совместного действия нагрузки q и силы Х1 равен нулю. Деформации балки, вызванные отдельно нагрузкой q и неизвестной силой Х1 изображены на рис. 9.6, б.

Для определения прогибов точки В можно воспользоваться любым из изложенных в М-8 методов.

При решении рассматриваемой задачи воспользуемся двумя метода- ми определения перемещений: методом начальных параметров (универ- сальное уравнение оси изогнутого бруса) и общей формулой перемещений (формулой Мора).

Используя метод начальных параметров, определяем прогиб конца консоли основной системы отдельно от нагрузки q и отдельно от силы X1:

Подставляя найденные значения прогибов в уравнение (9.1), получим

После определения «лишнего» неизвестного Х1 строятся окончатель- ные эпюры моментов и поперечных сил обычными методами как для ста- тически определимой балки (рис. 9.6, г).

В дальнейшем при составлении уравнений совместности деформа- ций типа (9.1) запись этих уравнений целесообразно вести с помощью обо- значения перемещений, имеющих стандартную (каноническую) форму. Принятую здесь методику обозначения перемещений будем применять и в дальнейшем. Напомним, что SP обозначает перемещение точки приложе- ния силы S по направлению действия этой силы от нагрузки, обозначаемой индексом Р; δmn обозначает перемещение по направлению действия силы m точки приложения этой силы, вызванное единичным силовым воздейст- вием, приложенным в точке n.

Перемещение по направлению действия момента обозначает угол поворота сечения, к которому приложен момент.

Рассмотрим решение приведенного выше примера с использованием введенных обозначений для перемещений.

Уравнение (9.1) в этом случае запишется так:

34

неизвестным усилием Х1;

D1Р – перемещение точки В в направлении действия силы Х1, вызван- ного нагрузкой Р. В данном случае под индексом Р подразумевается на- грузка q.

Перемещение от силы Х1 удобно представить в виде

1X1 = δ11X1,

где d11 – перемещение точки В основной системы в направлении действия Xl , вызванное единичным воздействием Х1 = 1. Таким образом, уравнение (9.2) принимает вид

Так как в дальнейшем при определении перемещений очень широко используется формула Мора, то покажем на этом примере порядок реше- ния статически неопределимых задач с использованием этой формулы.

Так, коэффициенты d11 и D1Р определяются по формулам

Индекс «s», стоящий внизу интеграла, означает, что интегрирование распространяется на все элементы системы.

Эпюры M1 и МP, как обычно, строятся со стороны растянутого во- локна (рис. 9.6, д).

Найдем коэффициенты уравнения (9.3), воспользовавшись правилом перемножения эпюр по Верещагину:

Здесь в круглых скобках выполнен подсчет площадей одной из пе- ремножаемых эпюр. Квадратными скобками выделены ординаты под цен- тром тяжести указанной площади, взятые из второй эпюры.

Так, при определении D1Р необходимо брать, как показано в М-8,

35

Далее строится исправленная эпюра моментов M1 Х1 (рис. 9.6, д). Ор- динаты окончательной эпюры моментов для статически неопределимой балки вычисляются по формуле

M = M P + M1X1,

т. е. они получаются как алгебраическая сумма ординат двух эпюр: МР и M1 Х1. Окончательная эпюра моментов представлена на рис. 9.6, г. Далее строится эпюра поперечных сил Q.

9.2. Канонические уравнения метода сил

Когда расчету подлежит сложная конструкция, имеющая более чем одну лишнюю связь, при выборе основной системы приходится отбрасы- вать как линейные, так и угловые связи. В этом случае составляется боль- шее количество уравнений совместности деформаций.

Физический смысл одних из этих уравнений может быть графически истолкован сравнительно просто, другие условия совместности не всегда могут быть просто и наглядно иллюстрированы. Тогда эти уравнения це- лесообразно записывать в каноническом виде.

Рассмотрим некоторый конкретный пример. На рис. 9.7, а представ- лена дважды статически неопределимая балка.

Один из возможных вариантов основной системы приведен на рис. 9.7, б. По этому варианту основной системы жесткое защемление опоры А заменяется шарнирно-неподвижной опорой и неизвестным моментом Х1. Правая опора С заменяется неизвестным усилием Х2. Уравнения деформа- ций в этом случае запишутся в виде

Смысл первого уравнения – отрицание угла поворота сечения балки у опоры А; смысл второго уравнения – отрицание перемещения точки С оси балки по вертикали.

36

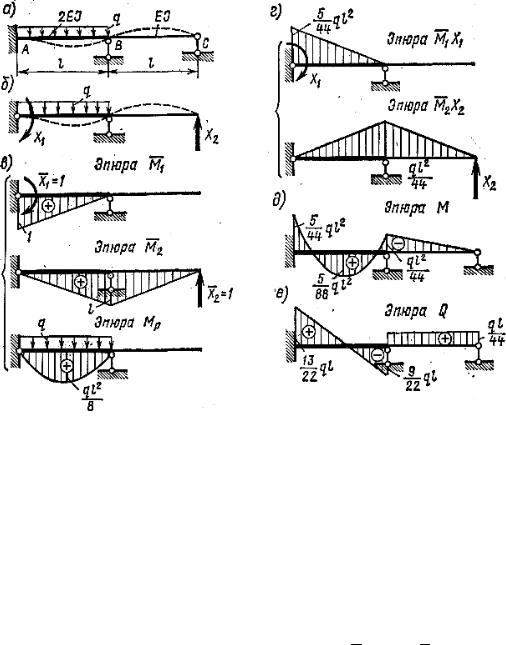
Рис. 9.7

На основании принципа независимости действия сил определяются перемещения от каждого из воздействий в отдельности и затем эти пере- мещения суммируются. Результат суммирования должен быть равен нулю, так как в заданной статически неопределимой балке угол поворота сечения у опоры А и вертикальное смещение точки С отсутствуют.

Перемещения от неизвестных Х1 и X2 удобно представить в виде:

1X1 = δ11X1 и 1X 2 = δ12 X 2 ,

где δ11 и δ12 – углы поворота сечения у опоры А основной системы, вы- званные единичными значениями неизвестных X1 = 1 и X 2 = 1.

Подстановка 1X1 и 1X 2 и, по аналогии, значений 2 X1 и 2 X 2 в

уравнения (9.4) дает

Полученные уравнения носят название канонических уравнений ме- тода сил. Число их равно степени статической неопределимости системы. За неизвестные в канонических уравнениях принимаются реактивные уси- лия или моменты в отброшенных связях. Именно поэтому приведенный метод решения называют методом сил.

37

Для определения перемещений δmn и SP строятся эпюры моментов в основной системе от единичных значений неизвестных X1 = 1 и X 2 = 1 и от внешней нагрузки Р. По формуле Мора путем перемножения соответст- вующих эпюр находят коэффициенты δmn и свободные члены SP канони- ческих уравнений. Далее решаются канонические уравнения и определя- ются неизвестные Х1 и Х2. После определения неизвестных балка превра- щается в статически определимую.

Проследим порядок расчета на рассматриваемом примере (рис. 9.7, а). Эпюры моментов в основной системе от единичных значений неизвестных X1 = 1 и X 2 = 1 и от нагрузки Р представлены на рис. 9.7, в.

Найдем коэффициенты и свободные члены канонических уравнений, считая, что жесткость на изгиб левого пролета 2EJ, а правого EJ:

Подстановка найденных значений коэффициентов и свободных чле- нов в канонические уравнения (9.5) и их решение дают:

Ординаты окончательной эпюры моментов для статически неопреде- лимой балки вычисляются по формуле

M = M P + M1X1 + M 2 X 2.

Исправленные эпюры M1 Х1 и M 2 Х2 показаны на рис. 9.7, г. Склады-

вая алгебраически ординаты эпюр МР, M1 Х1 и M 2 Х2, получим окончатель- ную эпюру моментов (рис. 9.7, д). Эпюра Q (рис. 9.7, е) строится как для простой статически определимой двухопорной балки, загруженной на- грузкой q, моментом X1 и силой Х2.

В строительной практике часто встречаются статически неопредели- мые балки, имеющие несколько промежуточных опор. Такие балки назы-

38

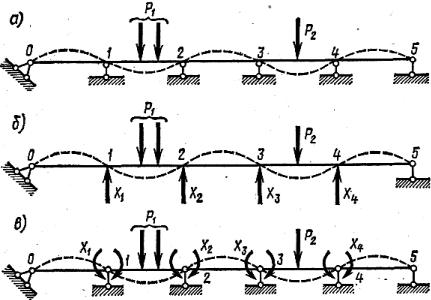
вают неразрезными. Весьма существенное значение при расчете таких ба- лок имеет рациональный выбор основной системы.

На рис. 9.8, а показана четыре раза статически неопределимая нераз- резная балка и два возможных варианта основной системы. По первому варианту основной системы (рис. 9.8, б) за неизвестные приняты величины опорных реакций Xl ..., Х4. Смысл канонических уравнений в этом случае состоит в отрицании перемещений точек 1, 2, 3, 4 оси балки по вертикали.

Во втором варианте основной системы (рис. 9.8, в) неразрезная балка превращается в пять простых двухопорных балок постановкой полных шарниров над промежуточными опорами.

В этом случае лишними неизвестными являются изгибающие мо- менты в сечениях балки над промежуточными опорами, и они будут опре- деляться из условия неразрывности балки над опорами. Смысл канониче- ских уравнений в этом случае состоит в отрицании углов раскрытия двух бесконечно близких сечений балки, взятых над промежуточными опорами.

Рис. 9.8

В обоих рассматриваемых вариантах решения получим систему со- вместных уравнений, число которых равно степени статической неопреде- лимости балки. Следует отметить, что по первому варианту каждое из уравнений системы содержит все n неизвестных. Это обстоятельство объ- ясняется тем, что от любого неизвестного перемещаются в основной сис- теме все точки, к которым приложены силы Х1 ..., X4.

Во втором варианте каждое уравнение содержит независимо от сте- пени статической неопределимости системы не более трех неизвестных, так как деформация, возникающая от любого из неизвестных, распростра- няется только в пределах двух прилегающих пролетов. Поэтому второй

39

вариант значительно проще, особенно для системы с большим числом не- известных.

Уравнения деформаций, составляемые для второго варианта, назы-

вают уравнениями трех моментов.

9.3. Расчет простейших статически неопределимых стержневых систем по методу сил

Метод сил, использованный при расчете статически неопределимых балок (п. 9.2), легко может быть распространен на расчет плоских стерж- невых статически неопределимых систем (рам, ферм, арок и др.). К пло- ским системам относятся такие системы, у которых все стержни и дейст- вующая на них нагрузка лежат в одной плоскости.

Рамные конструкции состоят из отдельных стержней, соединенных между собой жесткими узлами, вследствие чего изгиб одного из них вызы- вает деформацию других, прилегающих к нему стержней.

Выбор основной системы при расчете таких статически неопредели- мых систем методом сил производится так же, как и для рассмотренных выше статически неопределимых балок.

Основная система выбирается из заданной статически неопредели- мой путем отбрасывания лишних связей и замены их лишними неизвест- ными Xi. За лишние связи принимаются либо опорные реакции, либо внут- ренние силовые факторы. Основная система с приложенной нагрузкой и неизвестными реакциями отброшенных связей должна быть эквивалентна заданной системе.

Для каждой статически неопределимой конструкции можно выбрать несколько вариантов основной системы. Наиболее простой из них прини- мается для расчета.

Во всех случаях при выборе основной системы необходимо иметь в виду, что она должна быть статически определимой, геометрически неиз- меняемой (должна быть обеспечена ее кинематическая неизменяемость) и по возможности простой. Простота основной системы зависит от степени сложности построения в ней единичных эпюр и эпюр от внешней нагруз- ки, а также от сложности «перемножения» соответствующих эпюр при оп- ределении коэффициентов и свободных членов канонических уравнений.

Так, на рис. 9.9, а изображена дважды статически неопределимая рама. Три варианта основной системы для этой рамы показаны на рис. 9.9, б, в, г.

Во всех вариантах за лишние неизвестные принимаются усилия в от- брошенных связях. Третий вариант основной системы не может быть при-

40