
scherbo-sp2
.pdf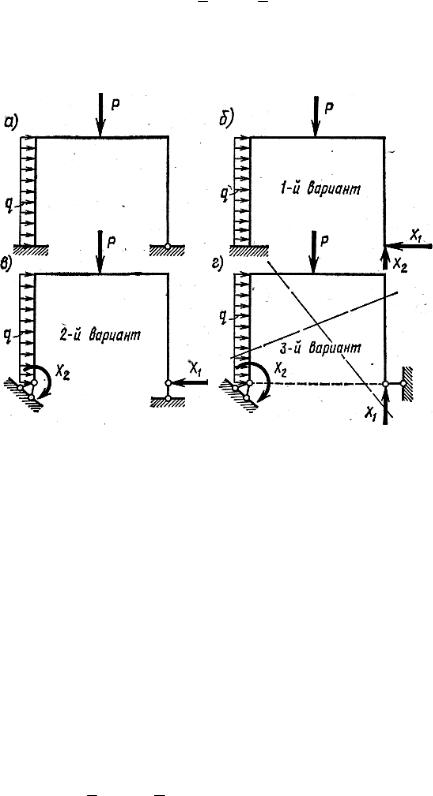
нят к расчету, так как система в этом случае является геометрически изме- няемой. Из сравнения первых двух вариантов наиболее простым будет 1-й вариант, так как построение эпюр моментов в основной системе от еди- ничных значений неизвестных X1 = 1, X 2 = 1 и приложенной нагрузки Р в
этом варианте проще, чем во 2-м варианте. Поэтому для расчета предпоч- тительнее принять 1-й вариант основной системы.
Рис. 9.9
Проследим на конкретных примерах применение метода сил к расче- ту простейших статически неопределимых стержневых систем.
Пример 1
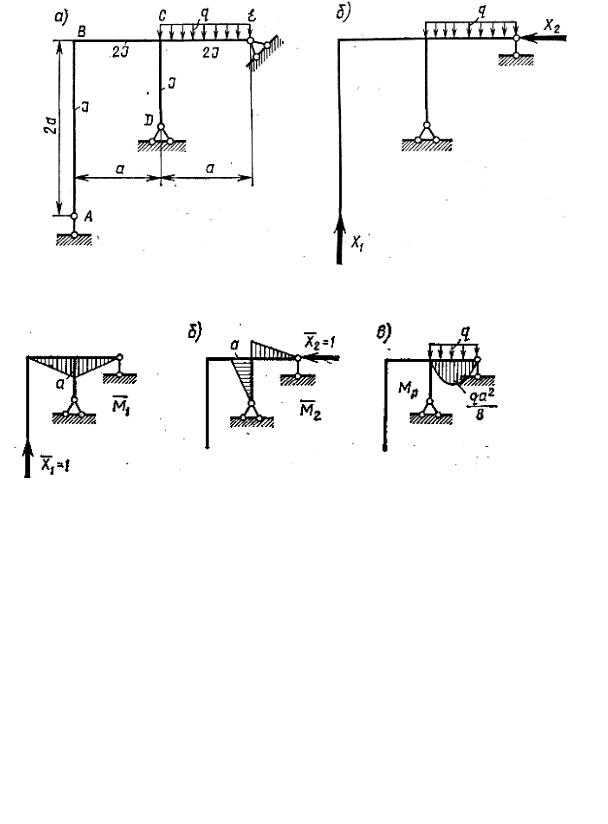
Построить эпюру изгибающих моментов, поперечных и продольных сил для рамы, изображенной на рис. 9.10, а. Рама два раза статически неопредели- ма. Один из возможных вариантов основной системы показан на рис. 9.10, б.
За неизвестные принимаются усилие в левой опоре Х1 и горизон- тальная составляющая правой опорной реакции Х2. Канонические уравне- ния для рассматриваемой рамы имеют вид:
δ11X1 + δ12 X 2 + 1P = 0;
δ21X1 + δ22 X 2 + 2P = 0.
Для определения коэффициентов и свободных членов канонических уравнений строим эпюры моментов в основной системе от единичных значе- ний неизвестных ( X1 = 1 и X 2 = 1) и от нагрузки Р (рис. 9.11, а, б, в).
41
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.10 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аа)) |
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.11
По формуле Мора, используя правило Верещагина, определяются ко- эффициенты уравнений, учитывая, что жесткость на изгиб горизонтальных элементов равна 2EJ, а вертикальных – EJ:
|
1 |
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
a3 |
|||||||||||||||||||||||||
d11 = |
|
|
|
a × a |
|
|
|
a |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
a × a |
|
|
|
a |
|
|
|
|
|
= |
|
|
|
; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
2 |
|
|
3 |
|
|
|
|
2EJ |
|
|
2 |
|
|
|
3 |
|
|
2EJ 3EJ |
|||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
2 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
a3 |
|||||||||||||||||||||||||||
d22 |
= |
|
|
|
a |
× a |
|
|
|
|
a |
|
|
|
|
|
|
+ |
|
|
|
|
|
a × a |
|
|
a |
|
|
|
|
|
= |
|
|
; |
||||||||||||||||||||||
2 |
|
|
|
|
EJ |
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2EJ 2EJ |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
d12 = d21 = - |
|
|
|
|
a |
× a |
|
|
|
a |
|
|
|
|
|
|
|
= - |
|
|
|
|
|
; |
|
|
|
|
|||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2EJ |
|
|
|
|
6EJ |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
D |
|
= |
|
2 |
|
a × |
qa2 |
|
|
a |
|
1 |
|
|
|
= |
|
qa4 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
1P |
|
|
3 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2EJ 48EJ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
qa2 |
|
|
a |
|
1 |
|
|
|
|
|
|
|
|
qa4 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
D |
|
= - |
|
|
|
|
a |
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= - |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||
|
|
|
2P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
48EJ |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2EJ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
42
Подставляем найденные значения коэффициентов в канонические
уравнения. После сокращения на |
1 |
и решения уравнений получим: |
|||||||
EJ |
|||||||||
|
|
|
|
|
|
|
|||
X1 |
= - |
qa |
; |
X 2 |
= |
qa |
. |
||
|
|
||||||||
|
20 |
|
|
40 |
|
||||
Далее строится окончательная эпюра моментов для заданной, стати- чески неопределимой рамы. Ординаты этой эпюры вычисляются по фор- муле
M = M P + M1X1 + M 2 X 2.
Для удобства построения эпюры М сначала строятся исправленные эпюры моментов M1X1 и M 2 X 2 и далее они алгебраически суммируются с эпюрой МР.
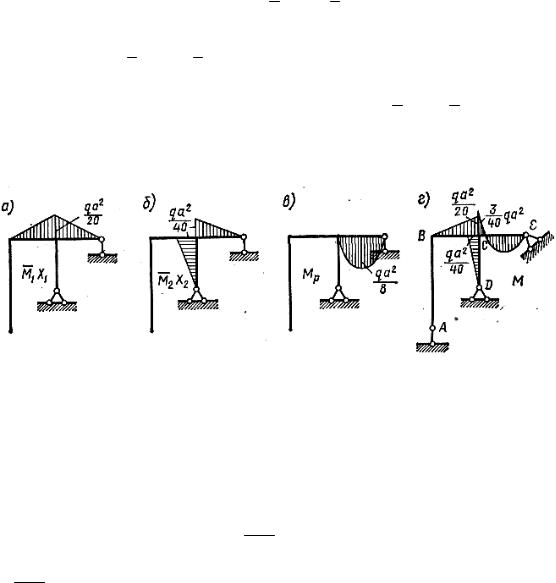
На рис. 9.12 показаны исправленные эпюры M1X1 , M 2 X 2 (рис. 9.12, а, б), грузовая эпюра МР (рис. 9.12, в) и окончательная эпюра моментов М
(рис. 9.12, г).
Рис. 9.12
Для построения эпюр поперечных и продольных сил можно восполь- зоваться принципом независимости действия сил и суммировать усилия, найденные отдельно от сил Р и полученных неизвестных Х1 и X2:
Для рассматриваемого примера эпюру Q следует строить исходя из дифференциальной зависимости
dM = Q, dz
где dM ¾ тангенс угла наклона, составляемый касательной к эпюре dz
моментов с осью стержня.
Удобно пользоваться следующим правилом знаков для поперечной силы: если ось стержня приходится вращать до совмещения с касательной к эпюре моментов по ходу часовой стрелки, то поперечная сила имеет знак плюс, и наоборот.
43
Для стержня СЕ (рис. 9.12, г), загруженного распределенной нагруз- кой, эпюра Q строится как в простой балке, загруженной нагрузкой q и
опорным моментом 3 qa2. 40
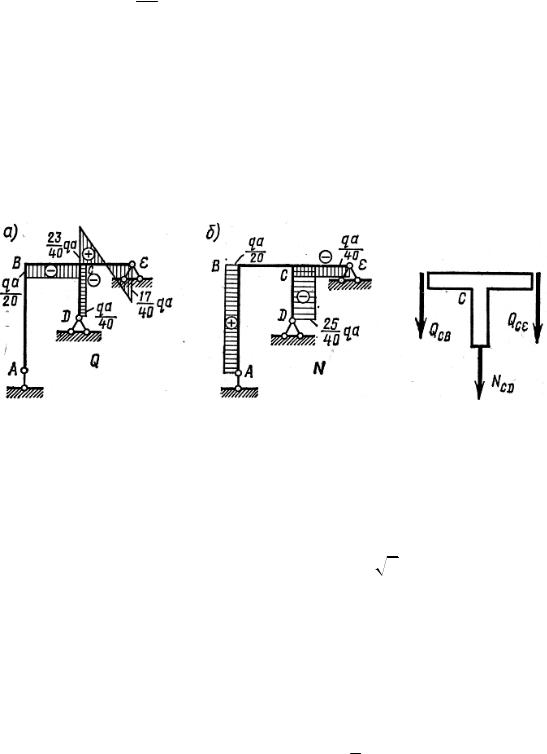
Эпюры Q и N представлены на рис. 9.13, а, б. Продольная сила в стержне АВ равна (−X1), в стержне ВС она равна 0, а в стержне CD − (−Х2). Из вырезания узла С находится продольная сила в стойке CD.
Рассматривая вырезанный узел в равновесии, получим (рис. 9.14):
∑ y = NCD + QCB + QCE = 0;
|
qa |
|
23 |
|
|
25 |
|
||
NCD |
= − |
|
+ |
|
qa |
= − |
|
qa. |
|
20 |
40 |
40 |
|||||||
|
|
|
|
|
|
||||
Рис. 9.13 |
Рис. 9.14 |
Пример 2
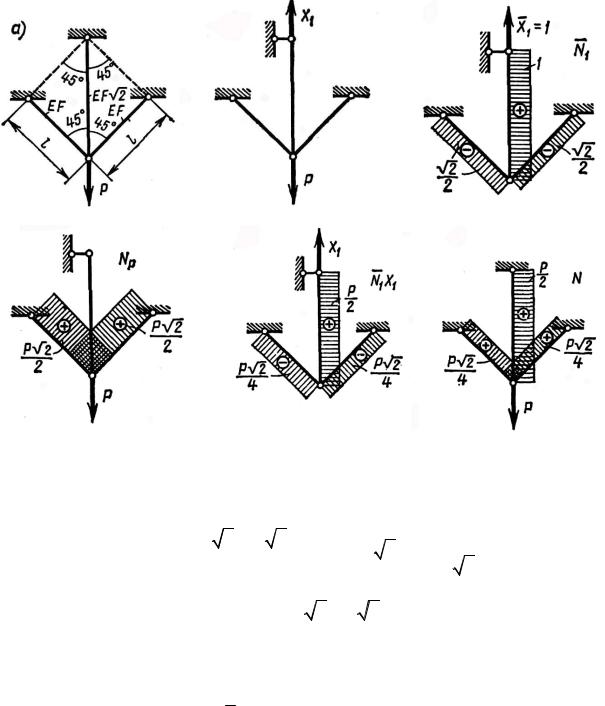
Три стержня, шарнирно соединенные по концам, загружены силой Р, как показано на рис. 9.15, а.
Найти усилия во всех стержнях, если жесткость на растяжение боко- вых стержней равна EF, а среднего стержня – EF 
 2. В данном случае все элементы системы имеют шарниры по концам и не загружены поперечной нагрузкой, т. е. они работают только на продольную силу. Задача один раз статически неопределима. Один из возможных вариантов основной систе- мы представлен на рис. 9.15, б.
2. В данном случае все элементы системы имеют шарниры по концам и не загружены поперечной нагрузкой, т. е. они работают только на продольную силу. Задача один раз статически неопределима. Один из возможных вариантов основной систе- мы представлен на рис. 9.15, б.
Каноническое уравнение запишется в виде
δ11X1 + |
|
1P = 0. |
(9.6) |
|
|
|
|
|
показаны на рис. 9.15, в, г. |
Единичная и грузовая эпюры |
N |
1 и NP |
||
Усилия в элементах основной системы от сил X1 = 1 и от силы Р определя- лись из уравнений статики способом вырезания узла.
44
а) |
|
б) |
|
в) |
|
|
|
|
|
|
|
|
|
|
г) |
|
|
|
е) |
|
д) |
|
||
|
|
|
|
|
|
|
|
|
|
Рис. 9.15
Коэффициенты канонического уравнения (9.6) определяются по фор- муле Мора:
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
2 |
|
1 |
+ (1×l 2 )[1] |
1 |
|
|
|
2l |
|
||||||||
d11 = ∫ |
N1 |
ds = 2 |
|
l |
|
|
|
|
= |
; |
||||||||||||
EF |
|
|
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
EF 2 |
|||||||||||||||||
s |
|
2 |
|
|
EF |
|
|
EF |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
P 2 |
|
2 |
|
1 |
|
Pl |
||||||
|
N |
P |
|
|
|
||||||||||||
D1P = ∫ |
1 |
ds = -2 |
|
|
|
l |
|
|
|
|
|
= - |
|
. |
|||
|
|
2 |
|
|
2 |
|
EF |
|
|||||||||
s |
|
EF |
|
|
|
|
|
|
|
|
EF |
||||||
Подстановка найденных значений d11 и D1Р в уравнение (9.6) и его решение дают Х1 = Р/2.
Исправленная эпюра N1 Х1 изображена на рис. 9.15, д. На рис. 9.15, е
показана окончательная эпюра продольных сил N.
Пример 3
Балка пролетом 2l, шарнирно опертая по концам, загружена сплош- ной равномерно распределенной нагрузкой q. Посередине балка дополни- тельно поддерживается упругой подвеской длиной l. Жесткость балки на изгиб EJ, жесткость подвески на растяжение E0F0 (рис. 9.16, а).
45
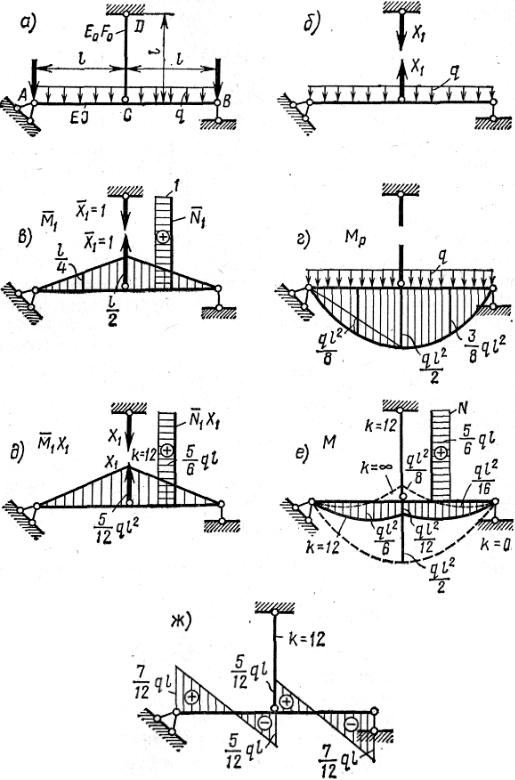
Рис. 9.16
Требуется построить эпюры М и Q для балки и эпюру N для подвес- ки. Система один раз статически неопределима.
Разрезая стержень CD, получаем основную систему (рис. 9.16, 6).
46

Каноническое уравнение запишется в виде
δ11X1 + 1P = 0.
Смысл канонического уравнения – отрицание взаимного смещения в на- правлении Х1 двух точек стержня CD в месте разреза.
Предложенная конструкция относится к категории комбинированных статически неопределимых систем, так как балка АВ работает на изгиб, а подвеска CD – на растяжение.
Для определения d11 и D1Р строятся единичные и грузовые эпюры моментов в основной системе (рис. 9.16, в, г). Кроме того, для стержня CD строится эпюра продольных сил от единичного значения неизвестного X1 =1, так как этот стержень работает на продольную силу и его деформа-
ция должна быть учтена при определении d11 и D1Р.
Определяем коэффициент канонического уравнения, перемножая, по Верещагину, не только эпюру изгибающих моментов, но и эпюру про- дольной силы от X1 =1:
d = 2 |
1 |
× |
l |
l |
2 |
× |
l |
|
1 |
+ (1×l )[1] |
1 |
= |
l3 |
+ |
|
l |
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
11 |
2 |
|
|
|
|
|
E0 F0 6EJ E0 F0 |
||||||||||||||
|
2 |
3 |
|
2 EJ |
|
||||||||||||||||
Для определения D1Р |
эпюру моментов на левой половине балки ра- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ql 2 |
|||
зобьем на треугольную и параболу с ординатой посередине |
|
|
|
. Далее от- |
|||||||||||||||||
8 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
дельно перемножим параболу, центр тяжести которой находится посере- дине, с треугольной эпюрой в M1 и отдельно треугольник из эпюры МР на треугольник в эпюре M1 и результат перемножения удвоим:
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
2 |
|
ql |
|
l |
1 |
|
1 |
|
ql |
|
|
2 |
|
l |
1 |
|
5 ql |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
D |
= -2 |
|
× |
|
|
l |
|
|
|
|
+ |
|
× |
|
|
l |
|
|
× |
|
|
|
|
= - |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1P |
|
3 |
|
8 |
|
|
2 |
|
2 |
|
|
|
|
EJ |
|
24 EJ |
|||||||||||||
|
|
|
|
4 |
EJ |
|
|
|
3 |
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приведенный способ перемножения эпюр не является единственным. Могут быть использованы и другие приемы, которые будут показаны в курсе «Строительная механика».
Далее определяем Х1:
X1 |
= |
|
5ql4 |
|
|
= |
|
|
5ql |
|
. |
||
|
l3 |
l |
|
|
|
|
6EJ |
|
|||||
|
|
|
|
|
|
||||||||
|
|
24EJ |
|
+ |
|
|
|
4 1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
6EJ |
E0 F0 |
|
|
|
|
l 2 E0 F0 |
|
|||
Введем обозначение
E0 F0 = k EJ2 , l
47

тогда
X1 |
= |
|
5ql |
|
|
. |
(9.7) |
|
|
|
+ |
6 |
|||||
|
4 |
1 |
|
|
|
|
||
|
|
|
|
|||||
|
|
|
|
|
k |
|
|
|
Ординаты окончательной эпюры моментов определяем по формуле
M = M P + M1X1.
На рис. 9.16, д показаны исправленные эпюры моментов M1X1 и
N1X1.
Далее, давая коэффициенту k различные значения, строим оконча- тельные эпюры моментов путем алгебраического суммирования ординат эпюр МР и M1X1 .
Рассмотрим три случая:
1) k = 0. Тогда из выражения (9.7) получим Х1 = 0, т. е. система рабо- тает как балка на двух опорах. Эпюра моментов для этого случая показана на рис. 9.16, е пунктиром;
2) k = ∞. Из равенства (9.7) получим X1 = 5 ql . В этом случае подвес- 4
ка превращается в жесткую шарнирно-подвижную опору. Эпюра момен- тов для такой балки показана также на рис. 9.16, е пунктиром;
3) k = 12. Из равенства (9.7) имеем X1 = 5 ql . 6
Суммируя исправленную эпюру моментов для случая k = 12 с эпю- рой моментов от нагрузки, получим окончательную эпюру моментов (рис. 9.16, е). Эпюра Q строится обычным порядком, как для статически определимой балки, загруженной нагрузкой q и найденной силой Х1 (рис. 9.16, ж). Эпюра N для подвески CD при k = 12 показана на рис. 9.16, е.
9.4. Расчет статически неопределимых балок по методу разрушающих нагрузок
При расчете балок по наибольшим напряжениям, возникающим в наиболее удаленном волокне, за опасное состояние принимается такое, при котором в наиболее напряженном сечении максимальные напряжения для пластического материала достигают предела текучести, а для хрупкого – предела прочности.
Однако легко заметить, что такое состояние балки не является опас- ным, так как во всех остальных волокнах поперечного сечения напряже- ние меньше опасного и поэтому грузоподъемность балки не исчерпана. Дальнейшее увеличение сил, действующих на балку, будет вызывать те-
48
кучесть в крайних волокнах и увеличение напряжений в соседних волок- нах до предела текучести.
При постепенном нарастании нагрузки эпюра напряжений в опасном сечении изменяется, проходя упругую и упруго-пластическую стадии. Грузоподъемность сечения при изгибе будет полностью исчерпана лишь в том случае, если образуется «пластический шарнир», т. е. напряжения по всему сечению будут равны σТ.
Для неразрезных балок образование одного пластического шарнира не вызывает их разрушения, так как грузоподъемность балки еще не пол- ностью исчерпана. Балка будет разрушена лишь тогда, когда в ней образу- ется несколько пластических шарниров, которые превращают балку в гео- метрически изменяемую систему.
Для расчета неразрезных балок по разрушающим нагрузкам прини- маем гипотезу об идеальной упруго-пластической работе материала. Со- гласно этой гипотезе напряжения в материале до предела текучести сле- дуют закону Гука, а площадка текучести принимается безграничной.
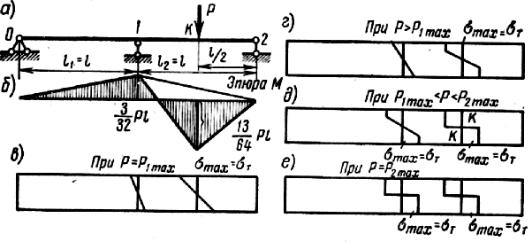
Рассмотрим частный пример неразрезной балки с двумя пролетами оди- наковой длины при действии одной сосредоточенной силы Р (рис. 9.17, а). Жесткость балки по длине принимается постоянной. Эпюра моментов при упругой работе балки, построенная по предложенной выше методике, по- казана на рис. 9.17, б.
Рис. 9.17
Как уже отмечалось, при расчете по допускаемым напряжениям наи- большая нагрузка, которая может быть допущена из условия появления первой текучести в наиболее напряженном месте (под грузом), определит- ся из выражения (рис. 9.17, в)
M |
|
= W σ |
13 |
P l, |
|
|
|||
|
max |
x T 64 |
1max |
|
49
откуда
P = |
64WxσT |
, |
(9.8) |
1max |
13l |
|
где Wx – момент сопротивления сечения относительно оси х.
Дальнейшее увеличение силы Р приводит к распространению пла- стических зон вглубь сечения (рис. 9.17, г) и появлению пластического шарнира в сечении К-К (рис. 9.17, д).
В этом случае балка превращается в статически определимую с промежуточным шарниром в сечении К-К, к которому приложены мо- мент Мраз и груз Р.
Таким образом, появление пластического шарнира не приводит к разрушению балки, а всего лишь снижает степень ее статической неопре- делимости на единицу.
При дальнейшем возрастании нагрузки будет увеличиваться момент над средней опорой и при Р = Р2 max в этом сечении также образуется пла- стический шарнир (рис. 9.17, е). Появление второго пластического шар- нира исчерпывает грузоподъемность балки, так как она превращается в геометрически изменяемую систему. Следовательно, разрушающая на- грузка должна быть подсчитана из условия появления двух пластических шарниров.
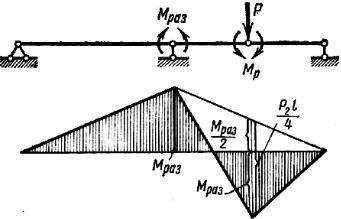
Схема балки и эпюра моментов в этом случае имеют вид, показан- ный на рис. 9.18.
Рис. 9.18
Разрушающая нагрузка определится из выражения
P2 maxl |
= |
3 |
M |
|
= |
2 |
W nσ , |
(9.9) |
|
|
раз |
|
|||||
4 |
2 |
|
3 |
T |
|
|||
|
|
|
|
|||||
где W n = 2Smax – для симметричного (относительно нейтральной оси) сечения;
50
