
scherbo-sp2
.pdf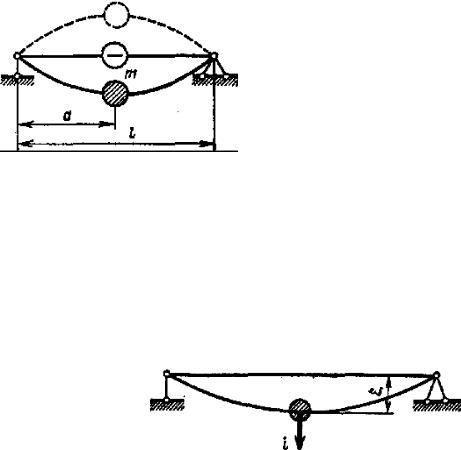
динамический прогиб в точке В
|
vВ = μvB |
|
= |
|
Gl |
3 |
μ; |
|
|
|
||||
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Д |
СТ |
|
26EJ1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
динамический прогиб в точке К |
|
|
|
|
|
|
|
|
|
|
|
|
||
v = μv |
|
|
|
l3 |
+ |
|
l3 |
|
|
μ. |
||||
|
= G |
|
1 |
|
|
1 |
|
|
||||||
КД |
|
КСТ |
|
12EJ |
1 |
|
|
48EJ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
Здесь следует обратить особое внимание на то, что во всех случаях бе- рется один и тот же динамический коэффициент. При определении последнего статический прогиб берется в той точке, по которой производится удар.
15.4. Собственные колебания системы с одной степенью свободы
Рассмотрим собственные колебания системы с одной степенью свобо- ды. Этот вопрос имеет большое значение для изучения динамических ха- рактеристик системы, которые используются в различных расчетах и в осо- бенности при действии вибрационной нагрузки.
Рассмотрим балку с сосредоточенной массой m, прикрепленной в ка- кой-либо точке на расстоянии а от левой опоры (рис. 15.13). Предположим, что мас- са самой балки по сравнению с массой m мала и ею можно пренебречь. Ось изогну- той балки определяется в этом случае вели- чиной отклонения массы, т. е. всего только одним параметром, поэтому такую балку называют системой с одной степенью сво- боды.
Если массу m отклонить от положе- ния равновесия и отпустить, то балка вместе с массой начнет колебаться. Такие колебания называют собственными, или свободными. Вследствие сил сопротивления колебания будут постепенно затухать и через некоторое время балка вновь придет в свое исходное положение.
Для того чтобы получить дифференциальное уравнение, описывающее колебания, рассмотрим движение массы в произвольный момент времени t
(рис. 15.14).
Рис. 15.14
181

Обозначим отклонение массы от первоначального положения через x. На массу действует сила инерции, которая, как известно, равна массе, по- множенной на ускорение, и направлена в сторону, противоположную уско- рению. Учтя, что ускорение определяется как вторая производная от пули, получим силу инерции, равную
i = -m |
d 2x |
. |
|
dt2 |
|||
|
|
||
Прогиб от этой силы можно найти так: |
|||
ξ = δ11i, |
(а) |
||
где d11 – прогиб от силы, равной единице, приложенной в точке прикре- |
|||
пления массы. Величину d11 легко определить любым из методов, опи- санных в М-8.
Подставив в уравнение (а) значение i, получим
|
|
x = -d |
m |
d 2x |
, |
(б) |
||||||
|
|
|
|
|
|
|||||||
11 |
|
dt |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
откуда |
|
|
|
|
|
|
|
|
||||
|
|
d 2x |
+ j2x = 0, |
|
(15.6) |
|||||||
|
|
|
|
|
||||||||
|
|
dt 2 |
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
||||
|
|
j2 = |
|
1 |
. |
|
|
|
(15.7) |
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
md |
|
|
|
|
|||
|
|
|
|
|
|
11 |
|
|
|
|
|
|
Как известно из курса дифференциальных уравнений, интеграл урав- |
||||||||||||
нения (15.6) имеет вид |
|
|
|
|
|
|
|
|
||||
ξ = A1 cos ϕt + A2 sin ϕt, |
(в) |
|||||||||||
где A1 и A2 – постоянные. |
|
|
|
|
|
|
|
|
||||
Уравнение (в) можно привести и к другому виду. Положим |
|
|||||||||||
A1 = Asin v; |
|
A2 = Acos v. |
|
|||||||||
Тогда для перемещений получим следующее уравнение: |
|
|||||||||||
|
x = Asin (jt + v). |
(15.8) |
||||||||||
Для скорости движущейся массы имеем |
|
|||||||||||
V = |
dξ |
= A ×jcos(jt + v). |
(15.9) |
|||||||||
|
||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|||
В уравнениях (15.8) и (15.9) содержатся две постоянные А и v, которые определяются из начальных условий.
Пусть при t = 0
ξ = ξ0 ,
dξ = V0. dt
182
Тогда из уравнений (15.8) и (15.9) имеем
Asin v = ξ0 ,
Aϕcos v = V0.
Решая эти уравнения, находим:
A = ξ2 + V0 2 ,
0 ϕ
v = arctgϕ ξ0 .
V0
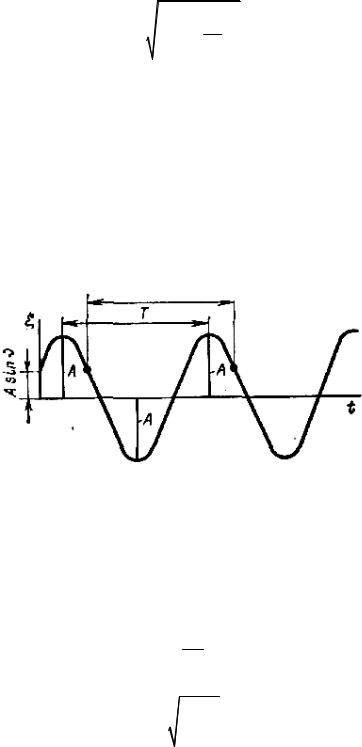
График изменения перемещения во времени показан на рис. 15.15. Наибольшее отклонение в ту или другую сторону будет тогда, когда sin(ϕt + v) принимает значение единицы. Как видно из уравнения (15.8), оно будет равно постоянной А. Таким образом, А представляет собой амплитуду колебаний. Время T, за которое совершается один полный цикл колебаний, называется периодом колебаний. Через каждые Т секунд отклонение ξ при- обретает прежнее значение.
Рис. 15.15
Из уравнения (15.6) имеем
ξ = Asin(ϕt + v) = Asin[ϕ(t + T ) + v].
Следовательно,
ϕT = 2π,
откуда число колебаний в 2π секунд равно
ϕ = 2π .
T
В соответствии с обозначениями выражения (15.7) имеем
ϕ = |
1 |
. |
(15.10) |
|
|||
|
mδ11 |
|
|
По формуле (15.10) и определяется теоретическое значение круговой частоты собственных колебаний (числа колебаний в 2π секунд) системы с одной степенью свободы.
183

Если масса m закреплена в середине пролета двухопорной балки, то прогиб δ11 от единичной силы, как известно, определяется равенством
δ11 = |
l3 |
||||
|
. |
||||
|
|||||
|
|
48EJ |
|||
Для данной задачи |
|
|
|
|
|
|
|
|
|
|
|
ϕ = |
48EJ |
. |
|||
|
|||||
|
|
ml3 |
|||
Из этой формулы видно, что частота колебаний увеличивается с уве- личением жесткости балки и уменьшается с увеличением пролета. Она так- же обратно пропорциональна массе m.
Если к балке прикреплено несколько, например п, масс, то система будет иметь n степеней свободы. В этом случае система имеет несколько собственных частот.
Приведенное выше решение является приближенным, так как в нем не учитывались силы сопротивления, например, сопротивления воздуха, силы трения в шарнирах, силы внутреннего сопротивления.
Силы сопротивления воздуха при скоростях колебаний, которые на- блюдаются в балках, невелики и поэтому их можно не учитывать. Силы трения в шарнирах могут быть устранены или сведены до минимума за счет улучшения конструкций шарнирных опор или их смазки.
Основными являются силы внутреннего неупругого сопротивления, которые зависят от материала балки и ряда других факторов. Эти силы уст- ранить невозможно.
По одной из наиболее распространенных гипотез учета затухания, предложенной Фойгтом, материал балки рассматривается как упруговязкое тело, в котором возникающие напряжения σ зависят не только от величины деформации ε, но и от скорости изменения деформации во времени:
σ = Eε + χE |
dε |
. |
(15.11) |
|
|||
|
dt |
|
|
Здесь χ для упруго-вязкого тела представляет некоторую константу, назы-
ваемую коэффициентом вязкого трения.
Указанная гипотеза приводит к тому, что эффект сил внутреннего со- противления при колебаниях рассматриваемой балки как системы с одной
степенью свободы заменяется действием внешней силы R = −k dξ (k – ко- dt
эффициент пропорциональности между силой и скоростью), приложенной в точке закрепления массы.
Гипотеза Фойгта удобна с точки зрения математического решения за- дачи, однако, как показали опыты, ее нельзя безоговорочно применять для учета неупругого сопротивления материалов при изучении колебаний упру-
184
гих систем. На этом вопросе остановимся дополнительно в п. 15.4 при рас- смотрении вынужденных колебаний системы с одной степенью свободы.
Для составления дифференциальных уравнений собственных колеба- ний системы с одной степенью свободы с учетом неупругих сил сопротив- ления вместо равенства (б) необходимо записать
ξ = −δ |
|
d 2ξ |
+ k |
dξ |
||
m |
|
|
|
, |
||
|
2 |
|
||||
11 |
|
dt |
|
|
|
|
|
|
|
|
dt |
||
откуда
|
|
|
|
d 2ξ |
+ 2β |
dξ |
+ ϕ2t |
= 0, |
|
(15.12) |
||||||||||
|
|
|
|
dt 2 |
|
dt |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2β = |
k |
; |
|
|
ϕ2 = |
|
1 |
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
mδ11 |
|
|
|||
Интеграл уравнений (15.12) можно записать в виде |
|
|||||||||||||||||||
|
|
|
|
ξ = Ae−βt sin(ϕ t + v), |
|
(15.13) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
ϕ = |
|
|
ϕ2 − β2 . |
|
(15.14) |
|||||||||
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
||
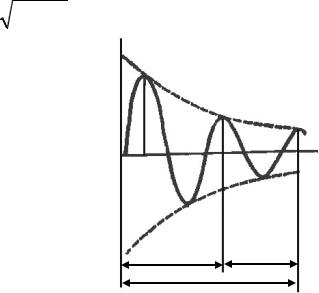
График колебаний (рис. 15.16), постро- |
ξ |
|
||||||||||||||||||
енный по выражению (15.13), показывает, что |
|
|
||||||||||||||||||
собственные колебания быстро затухают. Вы- |
|
|
||||||||||||||||||
ражение (15.14) дает значение частоты колеба- |
ξn |
ξn+1 |
||||||||||||||||||
ний с учетом сил сопротивления. Величина β |
|
|||||||||||||||||||
|
|
|||||||||||||||||||
обычно мала по сравнению с ϕ, поэтому ϕ* и ϕ, |
|
|
||||||||||||||||||
как правило, мало отличаются друг от друга: |
|
|
|
|
||||||||||||||||
|
|
ϕ* ≈ ϕ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для того чтобы оценить скорость зату- |
|
|
||||||||||||||||||
хания, найдем отношение |
двух |
отклонений |
tn |
T |
||||||||||||||||
массы, замеренных через один период Т (см. |
||||||||||||||||||||
tn+1 |
|
|||||||||||||||||||
рис. 15.16). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
e−βt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ξn |
|
|
|
|
|
βT |
|
|
|
|
|
|
|
|
Рис. 15.16 |
|
|||
|
|
= |
|
= e |
|
, |
|
|
|
|
|
|
|
|
|
|||||
|
ξn+1 |
e−β(t +T ) |
|
|
|
|
|
|
|
|
|
|
||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
ξn |
|
|
|
|
|||
|
|
|
|
|
|
|
|
βT = ln |
= γ. |
|
(15.15) |
|||||||||
|
|
|
|
|
|
|
|
ξn+1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Эту величину называют логарифмическим декрементом затухания; он характеризует скорость затухания собственных колебаний.
185

Наряду с теоретическими решениями широко проводятся экспери- ментальные исследования задач на колебания.
Для этой цели применяют самопишущие приборы. Такой прибор, бу- дучи прикрепленным к балке, записывает величины перемещений точки, к которой он прикреплен. График этих перемещений имеет вид, показанный на рис. 15.17. По горизонтальной оси этого графика прибор отмечает чер- точки, по которым можно установить продолжительность колебаний, а сле- довательно, и число колебаний в единицу времени, т. е. частоту колебаний.
ξ
t
Рис. 15.17
Таким образом, частоту собственных колебаний можно установить экспериментально.
Сравнение рис. 15.16 и 15.17 показывает полное совпадение картин затухающих колебаний, полученных теоретически и экспериментально.
15.5. Вынужденные колебания упругой системы
Если на систему действует сила Р (t), изменяющаяся во времени по какому-либо закону, то колебания балки, вызванные действием этой силы, называют вынужденными. После приложения силы инерции балку в от- клоненном состоянии можно рассматривать как находящуюся в равнове- сии (рис. 15.18). Перемещение ξ теперь уже нужно определить от двух сил – i и Р (t):
ξ = δ |
i + P (t ) , |
|
11 |
|
|
где δ11 – прогиб от единичной силы, массы.
ξ
приложенной в месте прикрепленной
P(t)
i = d 2ξ dt2
Рис. 15.18
186

Заменяя силу инерции ее значением и перенося неизвестные в левую часть, после деления всех членов на mδ11 получим
d |
2ξ |
+ ϕ2ξ = |
1 |
P(t). |
(15.16) |
dt 2 |
|
||||
|
m |
|
|||
Интеграл этого уравнения состоит из двух частей: решения однородно- го уравнения и частного интеграла, зависящего от вида правой части.
Рассмотрим частный случай, когда внешняя сила представляет собой вибрационную (периодическую) нагрузку, меняющуюся по гармоническому закону с частотой θ,
P(t) = P sin θt.
С учетом последнего равенства дифференциальное уравнение (15.16) примет вид
d |
2ξ |
|
P |
|
|
|
|
+ ϕ2ξ = |
|
sin θt. |
(15.17) |
dt 2 |
|
||||
|
m |
|
|||
Интеграл однородного уравнения нам уже известен из решения, полу- ченного в предыдущем пункте. Частный интеграл найдем в следующем виде:
ξ1 = C sin θt.
Подставляя это выражение в уравнение (15.17), определим
C = |
P |
= |
|
P |
|
|
. |
|
m(ϕ2 − θ2 ) |
mϕ2 |
|
− |
θ2 |
||||
|
|
|
1 |
|
|
|||
|
|
ϕ2 |
||||||
|
|
|
|
|
|
|
||
Если учесть, что
ϕ2 = 1 ,
mδ11
то получим C = Pδ11 . 1− θ2
ϕ2
Но так как Pδ11 = ξСТ – прогиб от статически приложенной силы Р, то
С = |
ξСТ |
|
. |
|
|
|
(15.18) |
||
|
|
|
|
|
|
||||
|
1− |
θ2 |
|
|
|
|
|
|
|
|
ϕ2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Таким образом, решение уравнения (15.17) имеет вид |
|
||||||||
ξ = Asin (ϕt + v) + |
|
ξCT |
|
sin θt. |
(15.19) |
||||
|
|
|
|||||||
|
|
1 − |
θ2 |
|
|
|
|||
|
|
ϕ2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
187
Первое слагаемое этого выражения представляет собой собственные колебания, а второе описывает вынужденные колебания. Величины А и v определяют из начальных условий.
Так как собственные колебания в реальных балках быстро затухают, то рассмотрим только вынужденные колебания, которые происходят с час- тотой θ.
Наибольшее отклонение стержня от своего первоначального поло- жения (т. е. амплитуда вынужденных колебаний) будет найдено, если при-
нять sin θ = 1:
ξmax = |
ξCT |
|
= ξCT |
μ. |
|
1 − |
θ2 |
|
|||
|
|
|
|
||
|
ϕ2 |
|
|
|
|
|
|
|
|
|
|
Для исследования значения динамического коэффициента
μ = |
1 |
|
|
1 − |
θ2 |
|
|
|
|
||
|
ϕ2 |
|
|
|
|
|
|
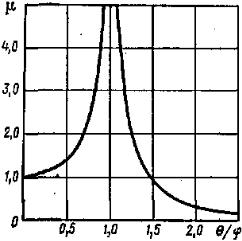
приведен график на рис. 15.19 абсолютного значения величины μ. Из этого графика видно, что в том случае, когда частота вынужденных колебаний θ приближается к частоте собственных коле- баний ϕ, динамический коэффициент μ без- гранично возрастает (при θ = ϕ μ → ∞). Та-
кое явление называется резонансом.
Если учесть затухание (силы внут- реннего сопротивления), то вместо уравне- ния (15.16) получим следующее дифференциальное уравнение:
d 2ξ |
|
dξ |
|
P |
|
|
+ 2β |
|
+ ϕ2ξ = |
|
sin θt. (15.20) |
dt 2 |
|
|
|||
1 dt |
|
m |
|||
Уравнение вынужденных колебаний Рис. 15.19 (15.20) отличается от уравнения собственных колебаний (15.12) не только наличием пра- вой части, но и коэффициентом при первой производной. Вместо величины
2β, введенной в уравнение (15.12), принят коэффициент 2β1.
Как уже говорилось в предыдущем пункте, гипотеза Фойгта не может быть безоговорочно принята при изучении колебаний упругих систем. Ее можно использовать при условии, что величина χ в формуле (15.11) не яв- ляется постоянной, а зависит от частоты колебаний. Результаты теории и опыта будут в большей мере согласованы, если принять, что при собствен-
188

ных колебаниях χ = χϕ = |
γ |
, а при установившихся вынужденных колеба- |
|||
2πϕ |
|||||
ниях, совершающихся с частотой θ, χ = χθ = |
γ |
. (Здесь γ – |
логарифмиче- |
||
|
|||||
2πθ |
|||||
ский декремент затухания.) Этим и объясняется то, что коэффициенты 2β и 2β1 в уравнениях (15.12) и (15.20), учитывающие влияние сил сопротивле- ния, различны.
Отношение двух коэффициентов β1 β будет такое же, |
как отношение |
χ0 χκ : |
|
β1 β = χθ χϕ = ϕ θ. |
(15.21) |
Частное решение уравнения (15.20), соответствующее чисто вынуж- |
|
денным колебаниям, может быть записано в виде |
|
ξ = B1 sin θt + B2 cos θt. |
(15.22) |
Подставляя это выражение в уравнение (15.20) и объединяя члены, со- держащие sin θt и cos θt, получим
|
|
|
P |
|
|
|
|
|
|
(ϕ2 |
− θ2 )B1 − 2β1θB2 |
− |
|
sin θt + |
2β1θB1 |
+ (ϕ2 |
− θ2 )B2 |
cos θt = 0. |
|
|
|||||||||
|
|
|
m |
|
|
|
|
|
|
Это уравнение должно тождественно обращаться в нуль при любых значениях t. Данное условие будет выполняться, если коэффициенты при sinθt и cosθt приравнять нулю. В результате получим два уравнения с двумя неизвестными В1 и B2:
(ϕ2 − θ2 )B1 − 2β1θB2 = P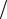 m; 2β1θB1 + (ϕ2 − θ2 )B2 = 0.
m; 2β1θB1 + (ϕ2 − θ2 )B2 = 0.
Решая полученные уравнения, найдем: |
|
|
|
|||||||||||
|
|
|
|
|
P |
(ϕ2 |
− θ2 ) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
= |
|
|
|
m |
|
||||||||
B1 |
|
|
|
|
|
|
|
|
|
, |
|
|||
( |
ϕ2 |
− θ2 |
) |
2 |
1 |
|
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
+ 4β2θ2 |
|
|
(15.23) |
||||||
|
|
|
|
|
|
|
P |
2β1θ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
= |
|
|
|
|
|
m |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
B2 |
|
(ϕ2 − θ2 ) |
2 |
|
|
. |
|
|||||||
|
|
|
|
+ 4β12θ2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее уравнение вынужденных колебаний (15.22) удобно представить
в виде |
|
ξ = B sin(θt + v1), |
(15.24) |
где В и v1 – амплитуда и фаза вынужденных колебаний.
189
Если учесть, что B sin(θt + v1) = B sin θt cos v1 + B cos θt sin v1, то легко ус-
тановить связь между постоянными: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
B1 = B cos v1; |
|
|
|
|
|
B2 = B sin v1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Возводя в квадрат левую и правую части этих равенств и складывая |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
их, найдем |
|
|
|
|
|
|
|
|
B2 = B2 |
+ B2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Но после деления левых и правых частей друг на друга получим |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
tgv1 = B2 |
B1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Учтя равенства (15.23), окончательно имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
B = |
|
B2 |
+ B2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
(ϕ2 − θ2 )2 + 4β1θ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
и |
|
|
|
|
|
|
|
v1 |
= arctg |
|
|
|
|
2β1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
θ2 |
− ϕ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
Pδ11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
P |
= |
= ϕ2ξ |
CТ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
m |
|
|
mδ11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
B = μξCT , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
где динамический коэффициент μ определится равенством |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
μ = |
|
|
|
|
|
|
ϕ2 |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
(15.25) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(ϕ |
2 |
− θ |
2 |
) |
2 |
+ |
2 |
θ |
2 |
|
|
|
|
|
|
|
θ |
2 |
|
|
2 |
|
|
|
|
|
|
θ |
2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
4β1 |
|
|
|
|
|
|
|
|
|
1 |
− |
|
|
|
|
+ 4β2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ϕ4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Используя равенства (15.21) и (15.15), найдем |
|
|
|
|
|
|
ϕ |
|
|
|
|
ϕ |
|
|
|
|
|
ϕ2 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β = β |
= βT |
= γ |
|
. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ |
θ |
2πθ |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя величину β1 в выражение |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(17.24), |
|
получим окончательную формулу |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
для динамического коэффициента |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μ = |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
. |
|
(15.26) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ2 2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ2 |
|
|
π2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
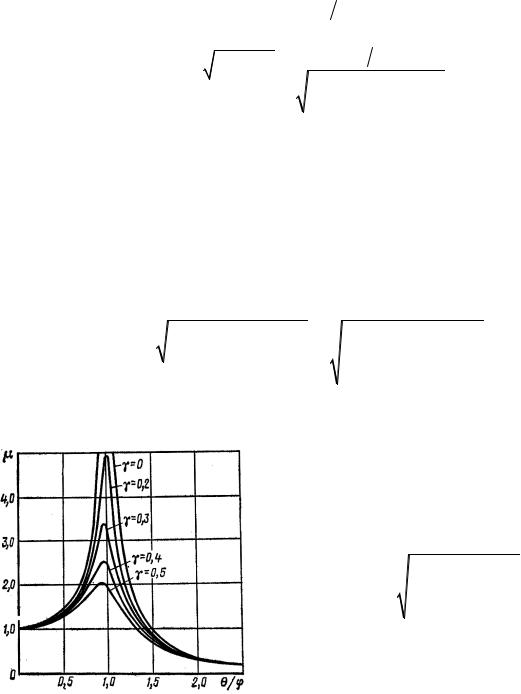
График |
|
|
изменения |
|
|
динамического |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
коэффициента, построенный по этому |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
выражению, имеет вид, показанный на |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
рис. 15.20. Положение каждой кривой за- |
|||||||||||||||||||||||||||||||||||||||||||
Рис. 15.20 |
|
|
|
|
|
|
|
|
|
висит от декремента затухания γ. |
Таким |
|||||||||||||||||||||||||||||||||||||||||||
190
