
scherbo-sp2
.pdf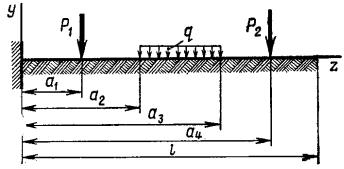
M n = M1 + ∑ MiY1(z − ai ) + ∑ |
|
Qi Y2 (z − ai ) + |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
qi |
|
|
|
|
|
|
qi′ |
|
|
|
|
|
|
|
|
+ ∑ |
|
Y3 (z − ai ) + ∑ |
|
Y4 (z − ai ); |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
β2 |
|
|
|
|
|
β3 |
|
|
|
|
|
|
|||
Qn = Q1 + ∑−4βΔMiY4 (z − ai ) + ∑ QiY1(z − ai ) + |
|
|
|
||||||||||||||
|
|
|
|||||||||||||||
|
|
|
qi |
|
|
|
|
|
qi′ |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
+ ∑ |
β |
|
Y2 (z − ai ) + ∑ |
β2 |
Y3 (z |
− ai ); |
|
|
|
(9.29) |
||||||
qn − kvn = q1 − kv1 + ∑−4βΔMiY3 (z − ai ) + |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||||
+∑−4βΔQ Y (z − a ) + |
|
|
|
|
|
|
′ |
|
|
|
|
||||||
∑ q Y (z − a ) + ∑ qi Y (z − a ); |
|
||||||||||||||||
|
i 4 |
|
|
|
i |
i 1 |
|
|
|
i |
|
β |
2 |
i |
|
|
|
′ |
′ |
|
′ |
|
|
′ |
+ ∑−4β |
3 |
|
MiY2 (z |
− ai ) + |
|
|
|
|||
|
|
|
|
|
|
|
|||||||||||
qn − kvn = q1 |
− kv1 |
|
|
|
|
||||||||||||
+∑−4β2 QiY3 (z − ai ) + ∑−4βΔqiY4 (z − ai ) + |
|
|
|
||||||||||||||
|
|
|
|||||||||||||||
+∑ |
′ |
(z − ai ). |
|
|
|
|
|
|
|
|
|
|
|
||||
qiY1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
В уравнениях (9.29) введены обозначения: |
M, |
Q, |
q и |
|
q′ – при- |
||||||||||||
ращения момента, поперечной силы, распределенной нагрузки и ee произ- водной на границах участков загружения; al a2, .... аn – расстояния от нача- ла координат до границ участков (рис. 9.24).
Рис. 9.24
На конце балки в начале координат при любом случае закрепления два начальных параметра известны. Для определения двух других посто- янных нужно удовлетворить граничным условиям на другом конце балки.
Так, для случая, показанного на рис. 9.24, из условий опирания левого конца балки имеем
′ |
= 0. |
v0 = 0, v0 |
Для определения М0 и Q0 воспользуемся условиями опирания балки на правом ее конце. Если правый конец свободно опирается на упругое ос- нование, то при z = l M (l) = 0 и Q(l) = 0.
61
Для примера представим эти уравнения в развернутом виде:
M (l) = M Y (l) + |
Q |
Y (l) − |
P |
Y (l − a ) − |
||
0 |
1 |
|||||
β |
β |
|||||
0 1 |
2 |
2 |
1 |
|||
− Pβ2 Y2 (l − a4 ) − βq2 Y3 (l − a2 ) + βq2 Y3 (l − a3 ) = 0;
Q(l) = −4βM Y (l) + Q Y (l) − PY (l − a ) − |
|||||
0 |
4 |
0 |
1 |
1 1 |
1 |
−P2Y1(l − a4 ) − βq Y2 (l − a2 ) + βq Y2 (l − a3 ) = 0.
Решая совместно два уравнения, найдем неизвестные М0 и Q0. Далее, пользуясь уравнениями (9.29), можно найти значения М, Q, v и v' на лю- бом из участков рассматриваемой балки.
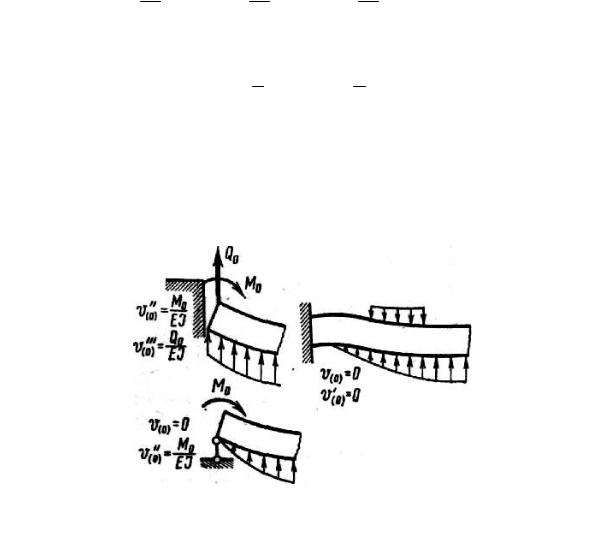
При других возможных случаях опирания концов балки граничные условия представлены на рис. 9.25.
Рис. 9.25
Преимуществом метода начальных параметров является то, что не- зависимо от числа участков загружения при определении произвольных постоянных для любого способа закрепления концов балки приходится решать лишь два уравнения с двумя неизвестными.
Для определения функций А.Н. Крылова обычно пользуются табли-
цами.
62
М-10. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
10.0. Введение в модуль
Модуль содержит следующие структурные элементы:
1.Общие понятия.
2.Построение эпюр внутренних усилий для стержня с ломаной осью.
3.Косой изгиб.
4.Одновременное действие изгиба и продольной силы.
5.Внецентренное действие продольной силы.
6.Ядро сечения.
7.Одновременное действие кручения с изгибом.
Цель модуля – изучить методику расчета прочности при косом из- гибе, вннецентренном сжатии, кручении с изгибом (сложном сопроттив- лении).
10.1.Общие понятия
Впредыдущих модулях рассматривались задачи, в которых брус ис- пытывал отдельно растяжение, сжатие, кручение или изгиб. На практике очень часто встречаются случаи, когда в результате действия нагрузки в поперечных сечениях бруса одновременно появляются перечисленные выше компоненты внутренних сил. Тогда говорят, что брус находится в условиях сложного сопротивления.
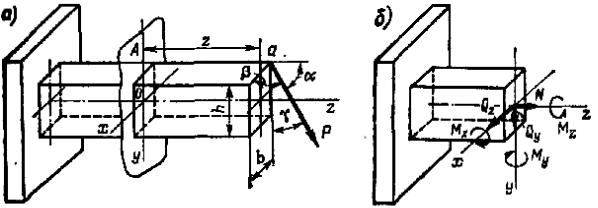
Рассмотрим действие силы Р в точке а, приложенной к брусу, заделанному одним концом (рис. 10.1, а).
а) |
|
б) |
|
|
|
|
|
|
Рис. 10.1
Проведем произвольное сечение плоскостью А и разместим в нем начало осей координат оxyz. Пусть направляющие углы между силой Р и указанными осями координат соответственно будут α, γ и β.
63
Нетрудно видеть, что от силы Р в произвольном сечении возникнут все шесть компонентов внутренних сил (рис. 10.1, б):
– нормальная сила
N= P cos α;
–поперечные силы, направленные вдоль осей oу и oх:
Qy = P cos γ;
Q[ = P cosβ;
– изгибающие моменты:
M x = −P h cos α − Px cos γ; 2
M y = −P b cos α − Px cosβ; 2
– крутящий момент
M z = P b cos γ − P h cosβ. 2 2
Нормальная сила и изгибающие моменты вызывают в точках попе- речного сечения нормальные напряжения. От поперечных сил и крутяще- го момента возникают касательные напряжения.
Для того чтобы определить суммарные напряжения, применяют принцип независимости действия сил, по которому, как известно, необхо- димо определить напряжения от каждого компонента внутренних сил в от- дельности, а затем их сложить. Для применения указанного метода прежде всего условимся относительно правила знаков.
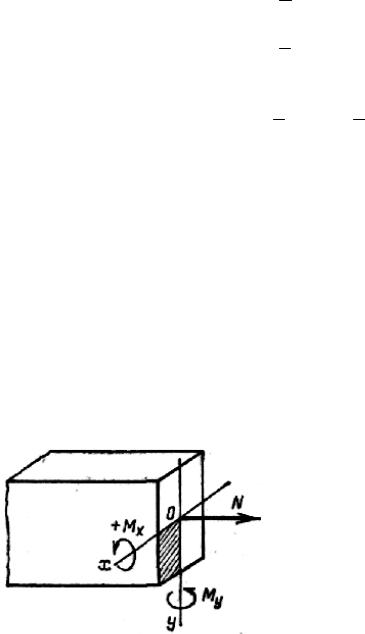
Нормальную силу, как и прежде, будем считать положительной, если она в рассматриваемом сечении вызывает растягивающие напряжения. Из- гибающие моменты примем положительными, если они в точках, принад- лежащих положительной четверти осей координат (совпадающих с глав- ными осями), вызывают растягивающие
напряжения.
На рис. 10.2 показаны оси коорди- нат oх и oу и им соответствующие поло- жительные направления моментов Мх и Му. На этом же рисунке показано положи- тельное направление нормальной силы N. Все три указанных фактора вызывают в точках, лежащих в положительной чет- верти, заштрихованной на чертеже, рас- тягивающие напряжения.
64

Так, при одновременном действии растяжения и изгиба в двух плос- костях нормальные напряжения в произвольной точке, лежащей в положи- тельной четверти поперечного сечения бруса, определяют по формуле
σ = |
N |
+ |
M |
x |
y + |
M y |
x. |
(а) |
|
|
|
J y |
|||||
|
F |
|
J x |
|
|
|||
Касательные напряжения складываются геометрически. Например, полное касательное напряжение в какой-либо точке при изгибе в двух плоскостях можно определить отдельно для каждого случая и затем их геометрически сложить:
τy |
= |
Qy Sxотс |
; |
||
J xby |
|||||
|
|
|
|||
τx |
= |
Q S отс |
; |
||
x |
y |
||||
|
|
|
|||
J ybx
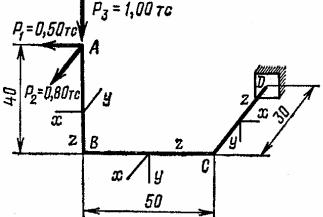
τ = 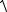
 τ2y + τ2x .
τ2y + τ2x .
Среди случаев сложного сопротивления стержней особое место за- нимают наиболее часто встречающиеся сочетания отдельных простейших видов нагружения, например, так называемого косого изгиба, внецентрен-
ного сжатия и одновременного действия кручения с изгибом.
Вместе с тем необходимо научиться определять внутренние силовыe факторы для стержней с пространственной осью.
10.2.Построение эпюр внутренних усилий для стержня
сломаной осью
При проектировании машин часто приходится рассчитывать брус, ось которого представляет собой пространственную линию, состоящую из отрезков прямых. Так, например, на рис. 10.3 показан брус, состоящий из трех стержней: АВ, ВС и CD. Два первых стержня лежат в одной плоско- сти, а стержень CD расположен в плоскости, нормальной к первой.
Расчет таких стержней начинается с определения внутренних сило- вых факторов в ряде сечений. Для отыскания наиболее напряженного (опасного) сечения строятся эпюры силовых факторов N, Mx, My, Мz, Qx, Qу. В первую очередь необходимо для каждого из стержней назначить оси координат. Обычно ось, совпадающую с осью бруса, обозначают осью oz, а две другие оси совмещают с главными осями инерции сечения.
Эпюры моментов и поперечных сил для каждого стержня строят, как для плоского бруса, с применением (для моментов) принятого ранее пра- вила знаков. При этом мысленно располагают каждый из стержней по от- ношению к себе так, чтобы взор был направлен в начало координат со сто- роны положительной оси oх (при построении эпюр Qy и Мх) или оси oу
65
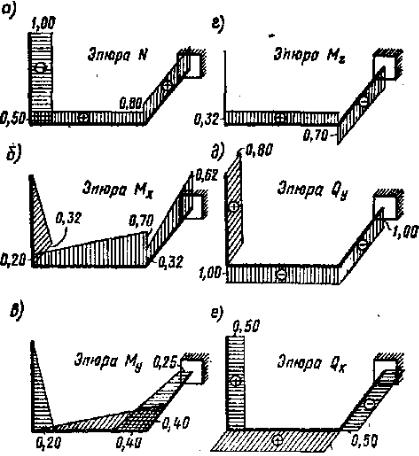
(при построении эпюр Qx и Му). Рассмотрим пример построения эпюр для бруса, изображенного на рис. 10.3, когда на него действуют три силы.
Рис. 10.3
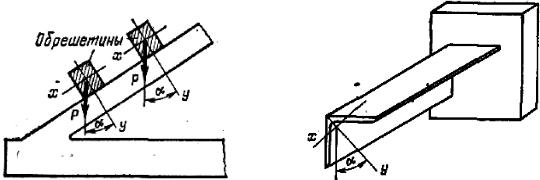
На рис. 10.4 показаны эпюры нормальных сил N, изгибающих мо- ментов Мх и Мy, крутящего момента Мz и поперечных сил Qy и Qx. Эти эпюры построены на основании вычисленных значений ординат для сече- ний, расположенных по концам каждого стержня. Крутящий момент будем считать положительным, если при взгляде на отсеченную часть со стороны сечения будет установлено, что момент Мz стремится повернуть сечение по ходу часовой стрелки.
Наиболее просто строится эпюра нормальных сил N. Рассекая стер- жень плоскостью, нормальной к его оси, и рассматривая равновесие отсе- ченной части, к которой приложены внешние силы, легко определить зна- чение нормальной силы. Для этого необходимо спроектировать все силы на ось соответствующего стержня и из уравнения ∑z = 0 определить силу N. Эпюра N показана на рис. 10.4, а.
Несколько сложнее определяются изгибающие моменты. Рассмотрим подробнее вычисление изгибающих моментов Мх. В стержне АВ изгиб относительно оси х вызывает только одна сила Р2, поэтому эпюра моментов имеет вид треугольника. Наибольший момент будет в нижнем сечении, проведенном через точку В. Так как через эту точку можно провести два сечения, одно из которых относится к вертикальному стержню, а другое – к горизонтальному, то в дальнейшем обозначим момент буквой М с двумя дополнительными индексами вверху. Первый верхний индекс показывает точку, через которую проведено сечение, а два индекса вместе определяют стержень, для которого находится изгибающий
момент. Например, M xba – момент относительно оси x в сечении, проведенном в точке В, но относящемся к стержню ВА; M xbc – момент в сечении В, проведенном вертикальной плоскостью в стержне ВС. Длины стержней
66
стью в стержне ВС. Длины стержней обозначим буквой l также с двумя индек- сами, определяющими концевые сечения стержня, например, lаЬ, lЬс и т. п.
|
|
|
|
|
Рис. 10.4 |
Таким образом, имеем: |
|||||
– |
для стержня АВ |
|
|||
|
|
|
|
M ba |
= P l = 0,80 ×0, 40 = 0,32 тc; |
|
|
|
|
x |
2 ab |
– |
для стержня ВС |
|
|||
M bc = -Pl |
= -0,50 ×0, 40 = -0,20 тc ×м (растянутое волокно вверху); |
||||
|
x |
1 ab |
|
|
|
– |
в точке С момент относительно оси х создают две силы: |
||||
M cb = -Pl |
- P l = -0,50 ×0, 40 -1,00 ×0,50 = -0,70 тc ×м; |
||||
|
x |
1 ab |
|
3 bc |
|
– для стержня CD |
|
||||
M cd = -P l |
|
= -0,80 ×0, 40 = -0,32 тc ×м; |
|||
|
x |
21 ab |
|
|
|
M dc = -P l |
|
- P l |
= -0,8 ×0, 4 -1,00 ×0,30 = -0,62 тc ×м. |
||
|
x |
21 ab |
3 cd |
|
|
По этим данным построена эпюра Мх, которая показана на рис. 10.4, б. Аналогичным образом построена эпюра Му (рис. 10.4, в).
Более просто вычисляются крутящие моменты. В стержне АВ кру- тящий момент равен нулю.
67
В стержне ВС |
|
|
|
M bc = P l |
= 0,32 тc ×м, |
||
z |
2 ab |
|
|
а в стержне CD |
|
|
|
M cd = -Pl |
- P l = -0, 70 тc × м. |
||
z |
1 ab |
|
3 bc |
По этим данным построена эпюра крутящих моментов (рис. 10.4, г). Поперечные силы Qx и Qy определяют как сумму проекций на оси х и
увсех сил, действующих на отсеченную часть.
Всоответствии с принятыми выше правилами знаков найдены попе- речные силы в стержнях и по ним построены эпюры, показанные на рис. 10.4, д, е.
Взависимости от размеров и формы сечений для каждого элемента бруса по формуле (а) п. 10.1 можно определить нормальные напряжения и
построить эпюру σ в заданном сечении. Суммарные касательные напряжения от двух поперечных сил Qy и Qx, а также от крутящего момента Мz должны быть получены путем геометрического суммирования.
10.3. Косой изгиб
Косым изгибом называется такой случай изгиба бруса, при котором плоскость действия суммарного изгибающего момента в сечении не сов- падает ни с одной из главных осей инерции. Короче говоря, в сечении воз- никают два изгибающих момента: Мх и Мy.
Так, например, обрешетины кровли (рис. 10.5) работают на косой изгиб. Вертикальная нагрузка от веса кровли и собственного веса обрешетины наклонена к главной оси под некоторым углом α.
Собственный вес уголка, заделанного одним концом в стену (рис. 10.6), также будет вызывать косой изгиб, так как главные оси сече- ния уголка наклонены по отношению к нагрузке под некоторым углом.
Рис. 10.5 |
Рис. 10.6 |
Рассмотрим отдельно ряд наиболее важных вопросов, связанных с расчетом стержней на косой изгиб.
68

1. Определение напряжений при косом изгибе. Рассмотрим балку,
заделанную одним концом, на которую действует сила Р, приложенная в центре тяжести концевого сечения под углом α к оси oу (рис. 10.7).
Рис. 10.7
Разложим силу Р на две составляющие по осям координат:
P = P cos α; |
|
|
y |
|
(10.1) |
|
|
|
P = P sin α. |
|
|
x |
|
|
Изгибающие моменты в сечении m-n относительно главных осей инерции в соответствии с установленным правилом знаков определяются равенствами:
M |
x |
= −P z = −Pz cos α; |
|
|
|
y |
|
(10.2) |
|
M |
y |
= −P z = −Pz sin α. |
|
|
|
x |
|
|
|
|
|
|
|
|
Таким образом, в каждом сечении стержня одновременно действуют два изгибающих момента, которые создают изгиб в двух главных плоскостях.
Для определения напряжений от каждого момента в отдельности можно воспользоваться формулой, полученной ранее для плоского изгиба. Пользуясь принципом независимости действия сил, можно написать об- щую формулу напряжения в произвольной точке, лежащей в положитель- ной четверти осей координат,
σ = |
M |
x |
y + |
M y |
x. |
(10.3) |
|
|
|
||||
|
J x J |
J y |
|
|
||
По формуле (10.3) можно определить напряжения в любой точке се- чения. Подставляя в эту формулу координаты какой-либо точки с учетом их знаков, получим значение напряжения в этой точке. Для угловых точек модули координат у и х приобретают максимальные значения, поэтому формулу (10.3) можно представить в виде
σ = ± M x ± M y .
Wx Wy
Здесь Wx и Wy – моменты сопротивления сечения.
69
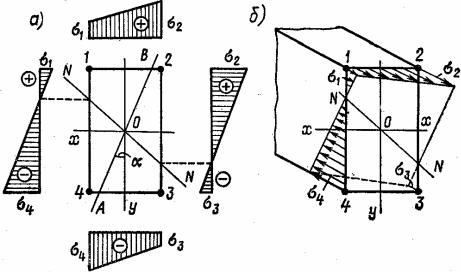
Для точек 1, 2, 3 и 4 (рис. 10.8), учитывая при определении знаков физический смысл задачи, можно записать:
σ = |
Py z |
− |
P z |
|
|
|
|||||||||
|
|
|
|
|
|
x |
; |
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
1 |
Wx |
|
|
Wy |
|
|
|||||||||
|
|
|
|
|
|
||||||||||
σ2 = |
|
Py z |
+ |
|
|
P z |
|
|
|
||||||
|
|
|
|
|
|
x |
; |
|
|
||||||
|
Wx |
Wy |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Py z |
|
|
|
P z |
|
|||||||
σ3 = − |
+ |
|
|||||||||||||
|
|
|
|
x |
|
; |
|
||||||||
W |
|
|
W |
|
|||||||||||
|
|
|
x |
|
|
|
y |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
σ4 = |
|
Py z |
− |
|
|
P z |
|
|
|
||||||
|
|
|
|
|
|
x |
. |
|
|||||||
|
Wx |
|
|
|
|||||||||||
|
|
|
|
|
|
Wy |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наибольшее растягивающее напряжение будет в точке шее сжимающее – в точке 4.
(10.4)
2, наиболь-
Рис. 10.8
Вычислив напряжения в четырех точках, можно построить эпюру напряжений. Существует два способа изображения эпюры при косом из- гибе. Первый заключается в том, что строят эпюры по граням сечения, как это показано на рис. 10.8, а. Снеся на грани сечения нулевые точки эпюр напряжений, можно провести нейтральную линию, или, иначе, нулевую линию NN, в которой напряжения во всех точках равны нулю. След АВ си- ловой плоскости пересекает нулевую линию NN под некоторым углом.
По второму способу строится пространственная эпюра напряжений, как показано на рис. 10.8, б. Вычислив наибольшие напряжения при косом изгибе, можно проверить прочность стержня, сравнивая полученное на- пряжение с расчетным сопротивлением.
70
