
scherbo-sp2
.pdf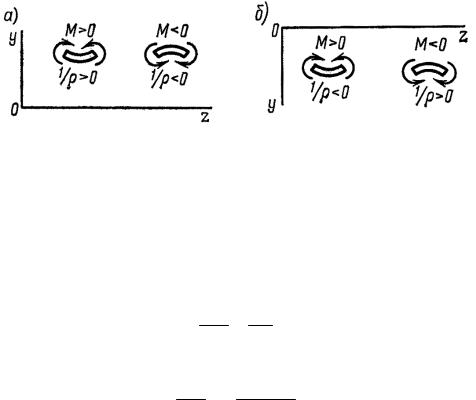
Интегрируя его первый раз, получим
dv |
= ±∫ |
M |
dz + C. |
(а) |
|
|
|||
dz |
EJ |
|
||
Это выражение определяет закон изменения углов поворота каса- тельной по длине балки.
После повторного интегрирования находим уравнение оси изогнуто- го бруса
v = ±∫∫ |
M |
dzdz + Cz + D. |
(б) |
|
|||
|
EJ |
|
|
Для вычисления интегралов, входящих в выражения (а) и (б), необ- ходимо сначала написать аналитические выражения изгибающего момента и жесткости. Постоянные интегрирования С и D находятся из граничных условий, которые зависят от способов закрепления бруса.
Для уяснения сказанного рассмотрим примеры.
1. Составим выражение прогиба и угла поворота в произвольном се- чении консольной балки, загруженной силой Р (рис. 8.6).
Рис. 8.6
Рассматривая равновесие правой отсеченной части, найдем
M = −P(l − z).
Знак минус взят потому, что нижние волокна балки сжаты. Так как ось оy направлена кверху, то в правой части дифференциального уравне- ния (8.5) надо взять знак плюс:
d 2v = M . dz2 EJ
Для нашего случая имеем
d 2v = − P(l − z) . dz2 EJ
Предположим, что жесткость балки постоянна. Интегрируя один раз, получим
dv |
= − |
Pl |
z + |
P |
z2 + C. |
(в) |
dz |
|
|
||||
|
EJ |
2EJ |
|
|||
11
Интегрируя еще раз, имеем
v = − |
Pl |
z2 + |
P |
z3 + Cz + D. |
(г) |
||
2EJ |
|
|
|||||
|
|
6EJ |
|
|
|
|
|
Так как в заделке прогиб и угол поворота равны нулю, то для опре- |
|||||||
деления постоянных будем иметь следующие граничные условия: |
|
||||||
при |
z = 0 |
dv |
= 0; |
|
|||
|
|
||||||
|
|
|
|
dz |
|
||
|
при |
z = 0 |
|
v = 0. |
|
||
Из уравнения (а) видно, что постоянная С представляет собой угол поворота в начале координат. Положив z = 0 , находим С = 0.
Из уравнения (г) следует, что постоянная D – это прогиб в начале ко- ординат. Положив в уравнении (г) z = 0 , получаем D = 0.
Итак, имеем:
v = − |
Plz2 |
+ |
|
Pz3 |
; |
|
|||||||
2EJ |
6EJ |
||||||||||||
|
|
|
|
|
|
|
|||||||
ϕ = |
dv |
= − |
Plz |
+ |
Pz2 |
. |
|||||||
|
|
|
|
||||||||||
|
dz |
|
EJ |
|
|
2EJ |
|||||||
Из рис. 8.6 видно, что наибольший прогиб будет под грузом. Поло- |
|||||||||||||
жив z = l , из первого уравнения найдем |
|
|
|
|
|
||||||||
|
v |
= − |
Pl3 |
. |
|
|
|||||||
l
3EJ
Угол поворота на конце балки
ϕl = − Pt 2 . 2EJ
Знак минус у прогиба свидетельствует о том, что его направление не совпадает с положительным направлением оси y, минус в выражении угла поворота показывает, что касательная не проходит в положительной чет- верти оси координат.
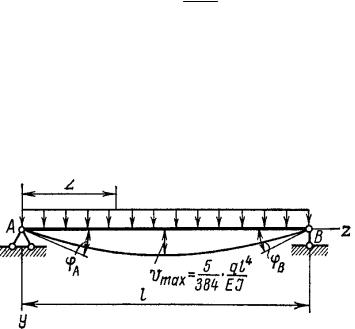
2. Определим прогибы двухопорной балки постоянного сечения, показанной на рис. 8.7.
Рис. 8.7
12

Так как ось y направлена вниз, то в дифференциальном уравнении необходимо взять знак минус:
|
|
|
d 2v |
|
= − |
M |
. |
|
|
|
|
|
|
||||||||||
|
|
|
dz2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
|
|
|
|
|||||||
Изгибающий момент в произвольном сечении равен |
|
||||||||||||||||||||||
|
M = |
qlz |
− |
qz2 |
. |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|||||
Таким образом, дифференциальное уравнение запишется в следую- |
|||||||||||||||||||||||
щем виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
EJ |
d 2v |
= − |
1 |
|
|
qlz + |
1 |
qz2. |
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
dz2 |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
Последовательное интегрирование дает: |
|
|
|||||||||||||||||||||
JEϕ = EJ |
|
dv |
= − |
|
qlz2 |
+ |
qz3 |
+ C; |
(д) |
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
dz |
|
|
|
|
|
4 |
|
6 |
|
|
||||||||||
EJv = − |
qlz3 |
+ |
qz4 |
|
+ Cz + D. |
(е) |
|||||||||||||||||
|
|
||||||||||||||||||||||
12 |
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|||||||
Для определения двух постоянных С и D необходимо иметь два ус- ловия. В рассматриваемом случае на левом и на правом концах прогиб ра- вен нулю. Таким образом, граничные условия равны: при z = 0 v = 0;
при z = l v = 0.
Подставляя в уравнение (е) z = 0 и приравнивая прогиб нулю, полу- чим D = 0; подставляя в это же уравнение z = l и также приравняв прогиб нулю, имеем
−ql 4 + ql4 + Cl = 0. 12 24
Следовательно,
C = ql3 . 24
Найденные значения постоянных подставим в уравнения (д) и (е) и получим уравнения прогибов и углов поворота:
EJ ϕ = EJ |
dv |
= |
ql3 |
− |
ql |
z2 + |
qz3 |
; |
|
|
|
|
|||||
|
dz 24 |
4 |
6 |
|
||||
EJv = ql3 z − ql z3 + qz4 . 24 12 24
Давая теперь абсциссе z определенные значения, получим численные величины прогибов и углов поворота в определенных сечениях балки. Та-
13

ким образом, можно вычислить прогиб и поворот сечения в середине про- лета, в четверти пролета и т. п.
Если в точке, где прогиб наибольший, функция прогибов имеет мак- симум, то для нахождения этой точки необходимо приравнять нулю пер- вую производную от v, т. е. выражение для угла поворота. В данной зада- че наибольший прогиб определяют из условия симметрии. Он находится посередине пролета. Положив z = l/2, получим
vmax = 5 ql 4 .
384 EJ
Если на различных участках балки момент (или жесткость) имеет раз- ные законы изменения, то необходимо составить несколько дифферен- циальных уравнений, каждое из которых отвечает своему участку. В соот- ветствии с этим число произвольных постоянных равно удвоенному числу участков интегрирования. Для определения постоянных всегда можно уста- новить условия на границах каждого участка (граничные условия). Так, на- пример, из условий непрерывности и гладкости оси изогнутого бруса выте- кает, что на левом конце какого-либо участка прогиб и угол поворота будут такими же, как на правом конце предшествующего участка.
Граничные условия приведут к системе уравнений, число которых соответствует числу постоянных. Совместное решение уравнений позво- лит найти постоянные и получить для каждого участка уравнение проги- бов и углов поворота. Однако необходимость решения совместных урав- нений очень сильно усложняет задачу, поэтому непосредственное интег- рирование применяют только в тех случаях, когда число участков невели- ко (один-два).
8.4. Метод начальных параметров
Задача определения прогибов может быть значительно упрощена, если применять так называемое универсальное уравнение оси изогнутого бруса или, как часто говорят, универсальное уравнение упругой линии. Вы-
вод универсального уравнения основан на так называемом методе началь- ных параметров, который широко применяют в строительной механике. По этому методу прогиб в любом сечении балки определяется через пе- ремещения и силовые факторы, взятые в начале координат с учетом при- ложенной к балке нагрузки.
Представим себе, что на брус действует произвольная система на- грузок, показанная на рис. 8.8, а.
14
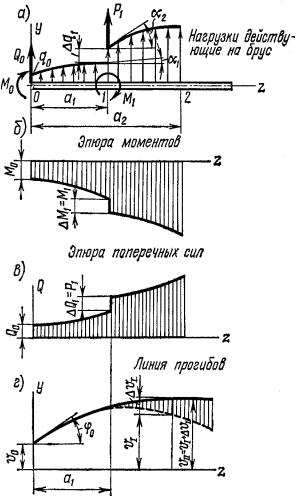
Интенсивность нагрузки и сосре- доточенные силы считают положи- тельными, если их направление совпа- дает с направлением оси оу, которую направим верх. Внешние сосредото- ченные моменты будут положительны, если они действуют по ходу часовой стрелки. Начало координат совместим с центром тяжести сечения на левом конце балки. Жесткость балки считают постоянной по всей ее длине.
Разобьем балку на ряд участков таким образом, чтобы на протяжении каждого участка изгибающий момент выражался с помощью непрерывной функции:
M I = M I (z);
M II = M II (z);
. . . . . . . . . . . . .
(Для упрощения записи в дальней- шем индексы у функций моментов и поперечных сил ставить не будем.) Граничные точки 1, 2, ..., разделяю- щие участки, должны быть поставле-
ны в тех сечениях, в которых происходят какие-либо изменения в законе распределения нагрузки. Так, например, имеется скачок в нагрузке q или изменяется закон ее распределения, приложен сосредоточенный момент, создающий скачок M = Mi , в эпюре моментов, или сосредоточенная си- ла P, создающая скачок в эпюре Q( Q = Pi ).
Рассмотрим сначала первый участок, прилегающий к началу коорди- нат, для которого согласно (8.5) дифференциальное уравнение имеет вид
|
|
d 2vI |
|
= |
M I |
. |
|
|
|
(а) |
|||
|
|
dz2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
EJ |
|
|
|
|
||||
Здесь vI – |
прогиб в произвольном сечении первого участка; |
|
|||||||||||
МI |
– функция, выражающая значение изгибающего момента в произ- |
||||||||||||
вольном сечении первого участка. |
|
|
|
|
|
|
|
|
|
|
|
||
Разложим функцию прогиба vI в ряд Маклорена: |
|
||||||||||||
|
′ |
′′ |
|
|
z2 |
|
′′′ |
z3 |
|
|
|||
|
(0) |
|
|
|
+ ... . |
(б) |
|||||||
|
vI = vI (0) + vI (0)z + vI |
|
|
|
+ vI (0) |
||||||||
|
|
|
|
|
2! |
|
|
3! |
|
|
|||
15
В этом уравнении величины vI (0); v′I (0); v"I (0) и т. п. представляют собой значения функции vI (z) и ее производных, взятые в начале коорди- нат, т. е. при z = 0.
Запишем дифференциальные зависимости:
|
|
|
|
dv |
|
= ϕ; |
d 2v |
= |
|
M |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
||||||||||||
|
|
|
|
|
dz2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
EJ |
|
|
|||||||||
|
|
|
3 |
|
|
|
|
|
1 |
|
|
dM |
|
|
|
Q |
|
|
|
||||||||
|
|
|
|
d v |
= |
|
|
|
= |
|
; |
|
|||||||||||||||
|
|
|
|
dz3 |
|
EJ |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
dz |
|
|
EJ |
|
(в) |
|||||||||||||
|
|
|
|
d 4v |
|
|
|
1 |
|
|
dQ = |
|
|
q ; |
|
||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
dz4 |
|
|
|
EJ dz |
|
|
|
|
|
EJ |
|
||||||||||||
|
|
|
|
d 5v |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
= |
|
|
|
dq |
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
dz |
5 |
|
|
EJ dz |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При дальнейшем дифференцировании имеем |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
d nv |
= |
|
|
1 |
|
d n−4q |
. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
dz |
n |
|
EJ dz |
n−4 |
|
|
|||||||||||||||
Положим z = 0 и обозначим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
vI (0) = v0 |
|
′ |
|
прогиб и угол поворота в начале координат; |
|||||||||||||||||||||||
и vI (0) = ϕ0 – |
|
||||||||||||||||||||||||||
M I (0) = M 0 |
и QI (0) = Q0 – |
|
момент и поперечная сила в сечении, взя- |
||||||||||||||||||||||||
том в начале координат; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
′ |
′′ |
′′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
q0 , q0 |
, q0 |
, q0 |
– интенсивность нагрузки и ее производные, взятые в |
||||||||||||||||||||||||
начале координат, т. е. при z = 0.
Тогда на основании дифференциальных зависимостей (в) между ко- эффициентами ряда Маклорена (б) и принятыми обозначениями имеем следующие равенства:
|
vI (0) = v0 ; |
′ |
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
M 0 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|||||||||||||||
|
vI |
(0) = ϕ0 ; vI (0) = |
EJ |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
||||
|
Q0 |
|
|
|
|
IV |
|
|
|
|
q0 |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
′′′ |
|
|
|
|
(0) = |
|
|
= |
|
q0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
; |
vI |
|
|
|
|
; vI (0) |
|
; ... |
и т. п. |
|
|
|
|
|||||||||||||||||||||||
vI = |
EJ |
|
|
EJ |
|
EJ |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставляя эти значения в уравнение (б), получим |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
M |
0 |
|
z |
2 |
|
Q0 z |
3 |
|
q0 z |
4 |
|
|
|
|
′ |
|
z |
5 |
|
|
′′ |
z |
6 |
|
|
||||||||||
vI = v0 + ϕ0 z + |
|
|
|
+ |
|
+ |
|
|
+ |
q0 |
|
|
+ |
q0 |
|
+ .... |
(8.6) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
EJ |
|
2! |
EJ 3! |
EJ 4! |
EJ 5! |
EJ 6! |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Полученное уравнение позволяет выразить прогибы в любом сече- нии первого участка через начальные параметры v0, ϕ0 М0, Q0 ... и т. д. Часть из этих параметров известна заранее, а часть подлежит определению из граничных условий.
Для того чтобы получить уравнение прогибов оси балки на втором участке, поступим следующим образом.
16
По уравнению (8.6), полученному для первого участка, построим ли- нию прогибов в пределах двух участков – первого и второго. На протяже- нии первого участка (рис. 8.8, г) она изображена жирной линией, на про- тяжении второго участка – пунктиром. Пунктирная линия представляет собой изображение линии, описанной уравнением (8.6), но она не совпада- ет с истинной кривой оси изогнутого бруса для второго участка, которая проведена жирной линией. Ординаты между двумя указанными кривыми изображены на заштрихованном участке чертежа. Аналитически эти орди- наты выражаются равенством
|
|
|
vI (z) = vII − vI . |
(г) |
|||||
Определим величину vI, а затем найдем ординаты прогибов балки |
|||||||||
на втором участке: |
|
vII = vI + vI . |
|
||||||
|
|
|
(д) |
||||||
Для этой цели напишем два дифференциальных уравнения: |
|
||||||||
|
d 2vI |
= |
M I |
; |
d 2vII |
= |
M II |
. |
|
|
dz2 |
|
dz2 |
|
|
||||
|
|
EJ |
|
EJ |
|
||||
Вычитая первое уравнение из второго, получим
d |
2 |
(v |
|
− v |
|
) = |
M |
II |
− M |
I |
. |
|
|
II |
I |
|
|
||||||
dz2 |
|
EJ |
|
||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
Обозначив
M I = M II − M I ,
имеем
d 2 vI |
= |
M I |
. |
(е) |
dz2 |
|
|||
|
EJ |
|
||
На основании сходства дифференциального уравнения (е) с основ- ным уравнением (а) можно утверждать, что решение для функции vI сов- падает с решением, полученным для функции (8.6).
В этом решении вместо координаты z придется теперь брать коорди- нату, отсчитанную от точки l, т. е. (z – а1). Вместо величин M0, Q0, q0, … и
т. д. придется брать |
М1; Q1; q1, ... . |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
(z − a ) |
|
|
|
|
||||||||
|
|
vI = |
v1 + Δϕ1 |
(z − a1) + |
|
M |
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
1 |
+ |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
2! |
|
|
|
|
(8.7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
||||
|
+ |
|
Q1 |
|
(z − a1) |
3 |
+ |
q1 (z − a1) |
4 |
+ |
q1 (z − a1) |
5 |
+ .... |
||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
EJ |
|
3! |
|
EJ |
|
|
4! |
|
EJ |
|
|
5! |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Здесь vI |
= vI (z) |
– функция, определяемая равенством (г) для второго |
|||||||||||||||||||||
участка (рис. 230, г); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
v1 – |
скачок в линии прогибов в точке 1 (на рис. 8.8, г не показан); |
||||||||||||||||||||||
Δϕ1 – |
скачок в угле поворота в точке 1 (на рис. 8.8, г не показан); |
||||||||||||||||||||||
17
М1 – скачок в эпюре моментов в точке 1 (рис. 8.8, б). Эта величина равна внешнему сосредоточенному моменту, приложенному в данной точке;
Q1 – |
скачок в эпюре поперечных сил (рис. 8.8, б), равный внешней |
||
сосредоточенной силе, приложенной в точке 1; |
|
|
|
q1 – |
скачок в интенсивности нагрузки в точке 1; |
|
|
q′1 – |
скачок в производной от интенсивности нагрузки в точке 1. |
||
Все перечисленные здесь величины скачков определяются как разно- |
|||
сти двух значений соответствующих величин, взятых в точке 1. |
|
||
Так, например, |
|
|
|
|
q1 = [qII (z) − qI (z)]z=a1 |
, |
(8.8) |
где qII (z) и qI (z) – функции, определяющие закон изменения распределен- ных нагрузок на втором и первом участках.
Величина q′1 |
определяется как разность производных. |
|
|||||||
|
q′ |
= [q′ |
(z) − q′ |
(z)] |
z=a1 |
= tgα |
2 |
− tgα . |
(8.9) |
Здесь α2 и α1 |
1 |
II |
I |
|
|
1 |
|
||
– углы наклона касательных к эпюре нагрузок, взятых |
|||||||||
в точке 1 (рис. 8.8, а). |
|
|
|
|
|
|
|
|
|
Скачок в угле |
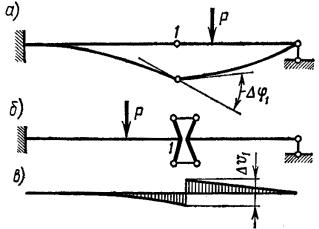
поворота может иметь место в случае, если в точке 1 |
||||||||
поставлен шарнир, из-за которого углы поворота слева и справа от точки 1 будут различны (рис. 8.9, а). Скачок в прогибах возможен в том случае, ес- ли в точке 1 балка разрезана на две части, которые соединены параллель- ными стерженьками, как это показано на рис. 8.9, б. Вследствие этого про- гибы двух балок в точке 1 будут отличаться друг от друга на v1, как это показано на эпюре прогибов (рис. 8.9, в).
Рис. 8.9
Для непрерывных балок, которые по всей длине, в том числе в точке 1, не имеют разрезов и полных шарниров, v1 = 0, Δϕ1 = 0. Если теперь учесть, что
18
vII |
= vI + |
vI , |
|
|
vIII |
= vII + |
vII = vI + ( vI + |
vII ), |
|
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
|
(ж) |
||
|
||||
|
n−1 |
|
|
|
|
|
|
||
vn = vI + ∑ vi , |
|
|||
|
|
|||
|
i=1 |
|
|
|
и вместе с тем воспользоваться уравнениями (8.6) и (8.7), то получим уни- версальное уравнение прогибов для произвольного участка
vn = v0 + ϕ0 z + |
M |
|
|
z |
2 |
|
|
Q |
|
|
z3 |
q |
|
|
|
z4 |
|
q′ |
|
z5 |
|
|
|||||||||||||
|
|
0 |
|
|
|
+ |
0 |
|
|
|
+ |
|
0 |
|
|
|
+ |
|
0 |
|
|
|
+ ... |
|
|
||||||||||
|
|
|
|
|
EJ 2! EJ 3! EJ 4! EJ 5! |
|
|
||||||||||||||||||||||||||||
n−1 |
|
n−1 |
|
|
|
|
|
|
|
|
|
|
|
n−1 |
M (z − a )2 |
+ |
|
(8.10) |
|||||||||||||||||
... + |
∑ |
vi + ∑ |
Δϕi (z − ai ) + ∑ |
|
|
i |
|
|
|
|
|
|
i |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
i=1 |
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
i=1 EJ |
|
2! |
|
|
|
|
|
|
|||||||||||
n−1 |
Qi |
|
(z − ai ) |
3 |
|
|
n−1 |
|
qi |
|
(z − ai ) |
4 |
|
|
|
n−1 |
|
qi′ |
|
(z − ai ) |
5 |
|
|||||||||||||
+ ∑ |
|
|
|
+ ∑ |
|
|
|
|
+ ∑ |
|
|
|
|
+ .... |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
i=1 |
|
EJ |
3! |
|
|
|
|
i=1 |
EJ |
4! |
|
|
|
|
|
i=1 |
EJ |
5! |
|
|
|||||||||||||||
Путем дифференцирования получим универсальное уравнение для углов поворота
|
|
|
|
M |
0 |
|
|
|
|
Q |
z2 |
q |
|
z3 |
|
q′ z4 |
|
|
|
|||||||||||
ϕn = ϕ0 |
+ |
|
z + |
|
|
0 |
|
|
|
+ |
0 |
|
|
+ |
|
0 |
|
|
|
+ ... + |
|
|||||||||
EJ |
|
|
|
|
|
EJ 4! |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
EJ 2! |
EJ 3! |
|
|
|
|
|||||||||||||||||
+∑Δϕi |
|
+ ∑ |
|
|
M |
i |
(z − ai ) + ∑ |
|
Q (z − a ) |
2 |
+ |
|
||||||||||||||||||
|
|
|
|
|
|
i |
|
|
|
i |
|
(8.11) |
||||||||||||||||||
|
|
EJ |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
2! |
|
|
|
|
||||||
+∑ |
qi |
|
(z − ai )3 |
|
+ ∑ |
qi′ |
|
(z − ai )4 |
|
+ .... |
|
|
|
|
||||||||||||||||
EJ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
3! |
|
|
|
|
|
|
|
EJ |
4! |
|
|
|
|
|
|
|
|
|
|
||||||||
При решении каких-либо частных задач целый ряд членов, входящих в уравнения (8.10) и (8.11), равен нулю. Полученные уравнения (8.10) и (8.11) зависят от величин v0, ϕ0, М0, Q0, q0, q′0 и т. п., которые берутся в на- чале координат, поэтому метод решения по указанным уравнениям носит название метода начальных параметров.
Из всех перечисленных начальных параметров некоторые параметры могут быть неизвестны. Величины q0 и q′0 по условию задачи обычно зада- ны. М0 и Q0 могут быть известны или должны быть определены из условий статики, а в тех случаях, когда задача статически неопределима, – из усло- вия деформаций. Величины v0 и ϕ0 не могут быть определены из условий статического равновесия. Определение этих начальных параметров произ- водят по граничным условиям. Так, например, для балки, показанной на рис. 8.10, a, в начале координат v0 и ϕ0 не равны нулю. Они могут быть оп- ределены из условия равенства нулю прогибов на опорах а и b.
19
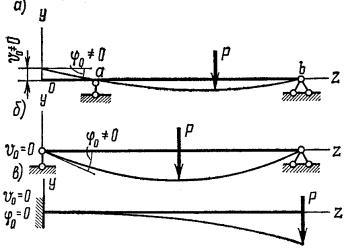
Рис. 8.10
Основное преимущество метода начальных параметров состоит именно в том, что независимо от числа участков и нагрузки число посто- янных, которые надо определить в статически определимой балке, не пре- вышает двух.
Для балки, изображенной на рис. 8.10, б, начальный прогиб равен нулю, неизвестным остается начальный угол поворота ϕ0. Для eго опреде- ления надо использовать условие равенства нулю прогиба на правой опоре. Для случая, представленного на рис. 8.10, в, начальный прогиб и началь- ный угол поворота равны нулю.
После того как будут найдены начальные параметры, можно напи- сать окончательные аналитические выражения прогибов и углов поворота для каждого участка балки. Придавая величине z ряд значений и вычисляя в соответствующих точках численные значения прогибов и углов поворо- та, можно построить линию прогибов и линию углов поворота оси балки.
Втехнических задачах часто ставится вопрос об определении места
ивеличины наибольшего прогиба балки. Для определения местоположе- ния сечения, в котором прогиб приобретает наибольшее значение, необ- ходимо приравнять нулю производную:
dv |
= ϕ = 0 , |
(8.12) |
|
||
dz |
|
|
откуда можно определить абсциссу наибольшего прогиба.
В некоторых случаях наибольший прогиб не совпадает с экстремаль- ным значением функции, так, в случае, показанном на рис. 8.10, в в месте наибольшего прогиба условие (8.12) не выполняется. Тогда приходится исходить из общей картины возможных деформаций системы и определять место наибольшего прогиба путем анализа всей линии прогибов.
Рассмотрим ряд примеров применения универсального уравнения для определения перемещений в балке при изгибе.
20
