
scherbo-sp2
.pdf



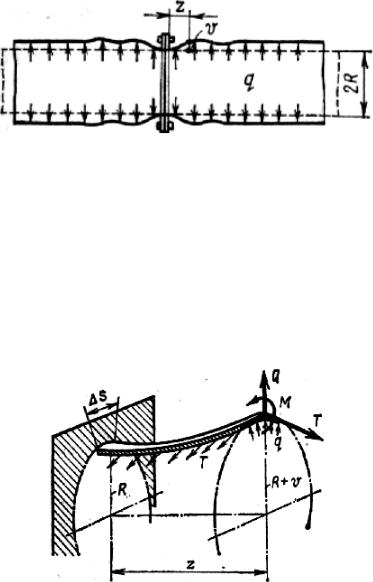
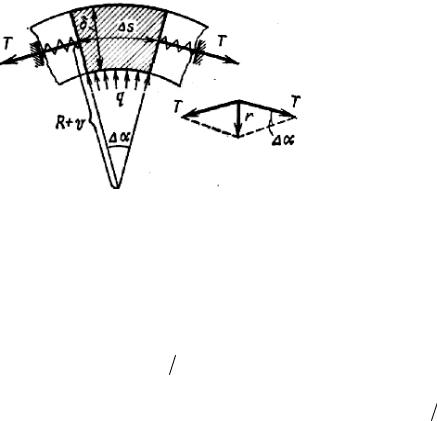
Внешнюю нагрузку на эту балку прежде всего создает внутреннее давление, которое на единицу длины полоски при Ds = 1 даст нагрузку q ×1Ds = q. Кроме того, в продольных сечениях трубы действуют окружные усилия, величину которых на единицу длины полоски обозначим через Т. Величина этих усилий пропорциональна упругому относительному удлине- нию колец трубы, образованных поперечными сечениями. Поэтому на рис. 18.12, где изображено поперечное сечение полоски, силы Т условно показаны как упругие реакции воображаемых пружин. Они дают равнодей- ствующую r, которую можно рассматривать как нагрузку на балку-полоску.
Рис. 18.12
Из рис. 18.12 найдем
r = 2T sin Δα » T |
s |
, |
|
||
2 |
R + v |
|
или, пренебрегая в знаменателе величиной v по сравнению с R и учитывая, что Ds = 1, получим
r = T R. |
(18.12) |
|||
Относительное удлинение радиуса R, а следовательно, и относитель- |
||||
ное удлинение стенок трубы в окружном направлении составит εt |
= v R. |
|||
Соответствующие окружные напряжения по закону Гука равны st |
= |
v |
E. |
|
|
||||
|
|
|
R |
|
Отсюда |
|
|
|
|
T = s d ×1 = δE v, |
|
|
|
|
1 |
R |
|
|
|
и, следовательно, |
|
|
|
|
|
|
|
|
|
r = δE v. |
(18.13) |
|||
|
R2 |
|
|
|
Формула (18.13) показывает, что усилия r можно рассматривать как реакцию упругого основания, сопротивляющегося прогибам v балки- полоски с коэффициентом пропорциональности
230
