
студ ивт 22 материалы к курсу физики / belonuchkin_ve_zaikin_da_tsipeniuk_ium_kurs_obshchei_fiziki
.pdf4.2 ] |
Движение частицы в поле «прямоугольной ступеньки» |
71 |
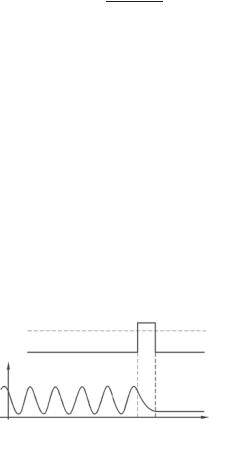
Рассмотрим теперь случай надбарьерного прохождения частицы массы , (при этом ее энергия должна быть больше высоты ступеньки 0). Решение уравнения Шрёдингера
|
|
|
2 |
0 0 |
|
|
|||||||||
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
аналогично предыдущему, и мы получаем |
|
|
|
|
|||||||||||
0 |
2 |
0, |
1 1 1 ; |
||||||||||||
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
2 |
|
0, |
2 |
2 |
, |
|||||||||
2 |
|||||||||||||||
|
|
0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где введены обозначения |
|
|
|
|
|
|
|
||||||||
2 |
|
2 |
2 2 |
|
|
|
|
||||||||
1 |
|
, |
2 |
|
0 |
|
|
||||||||
2 |
2 |
|
|||||||||||||
Производим сшивку решений:
1 0 2 0 |
1 ; |
||
|
0 |
0 |
1 1 2 |
1 |
2 |
|
|
(4.43)
(4.44)
(4.45)
(4.46)
Отсюда легко найти выражение для амплитуды прошедшей волны:
1, |
|
|
1 , 2 1 |
(4.47) |
|
|
1 |
1 |
2 |
|
|
1 2
Таким образом, теперь, в отличие от подбарьерного отражения, волна частично отражается, а частично проходит над барьером. Для характеристики этого явления вводится коэффициент прохождения , равный отношению потоков 2 1 прошедшей и падающей волн.
Поток, как известно, равен произведению (т. е. скорости на плотность). В области 0 кинетическая энергия части-
цы |
1 |
2 |
2 |
, |
а в |
области |
0 — |
2 |
2 |
||
|
|
1 |
|
|
|
|
|
2 |
2 |
|
|
0. Вспомнив, |
что, |
согласно |
введенным обозначениям, |
||||||||
2 |
2 |
2 , |
а |
|
2 |
2 |
2 , получим |
следующее |
|||
|
1 |
|
0 2 |
|
|||||||
выражение для отношения скоростей: 2 1 2 1. Кроме того, так как амплитуда падающей волны нами принята равной еди-
нице, то |
|
1 |
2 |
. Таким образом |
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
2 |
2 |
|
2 |
|
(4.48) |
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
1 |
1 |
|
1 |
|
|
Следовательно, несмотря на то, что энергия частицы больше высоты ступеньки, имеется не только прошедшая, но и отраженная волна, то есть частица «неполностью» проходит над
72 |
Уравнение Шрёдингера. Туннельный эффект |
[ Гл. 4 |
ступенькой. В самом деле, коэффициент прохождения равен
4 1 2 2 ,
1 2
а коэффициент отражения
|
1 |
2 |
2 |
|
|
|
|||
1 |
2 |
|||
|
|
При этом 1. Полученный результат существенно отличается от соответствующего результата классической механики, согласно которой в случае 0 всегда 1, а 0. В квантовой механике, как мы видим, коэффициент прохождения равен единице только при 1 2, но последнее означает, что ступеньки просто нет. Необходимо также заметить, что смена направления движения частицы не влияет на ответ в силу симметричности полученного решения.
4.3. Прямоугольный барьер. Туннельный эффект
Теперь мы легко можем рассмотреть задачу о прохождении частицы под прямоугольным барьером конечной ширины (рис. 4.4).
Полная энергия |
U0 E |
||
|
|
|
U(x) |
| (x)|2 |
0 |
|
a |
I |
II |
III |
|
|
|
|
| III |2 = const |
Падающая |
|
|
Прошедшая |
и отраженная волны |
|
волна |
|
Рис. 4.4
Запишем уравнение Шрёдингера в различных областях, как это делалось выше:
область I и III |
2 |
|
|
|
2 |
0, |
|
|
|
(4.49) |
||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
область II |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
0 |
(4.50) |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решения этих уравнений имеют вид |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
I |
1 2 |
2 , |
|
|
|
2 , |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III |
(4.51) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
2 0 2 0 |
(4.52) |
|||||||||||||||||||||
II |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4.3 ] |
Прямоугольный барьер. Туннельный эффект |
73 |
Здесь — амплитуда отраженной волны, амплитуда падающей волны принята равной 1, — амплитуда волны, прошедшей в область III («сквозь» барьер), и — амплитуды двух вещественных экспонент, через которые выражается волновая функция в области II (под барьером).
Коэффициент прозрачности барьера представляет собой отношение потоков вероятностей прошедшей и падающей волн:
2 |
(4.53) |
Нетрудно показать, что за исключением случая, когда энергия частицы мало отличается от высоты барьера, определяющим в (4.52) является второй член, т. е. . Иными словами, можно считать, что в области II, под барьером, волновая функция спадает экспоненциально:
2 0 |
|
(4.54) |
II |
|
|
Тогда коэффициент прозрачности сотой 0 и шириной можно (4.54):
2
II
прямоугольного барьера выполучить непосредственно из
2 2 0 |
(4.55) |
Полученный результат легко обобщается на случай барьера произвольной формы, который можно разбить на ряд прямоугольных барьеров (рис. 4.5).
Суммируя действие этих элементарных барьеров, получим
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|||
|
2 |
(4.56) |
|||||
|
|
|
|
||||
|
|
||||||
1
Строго говоря, под знаком корня должна стоять приведенная масса
,
где — масса тела, образую- |
|
||
щего потенциальный барьер. |
|
||
Прохождение |
частицы |
под |
|
потенциальным барьером |
пред- |
|
|
ставляется на |
первый взгляд |
|
|
парадоксальным. |
Действитель- |
Рис. 4.5 |
|
но, частица, находящаяся внутри потенциального барьера при полной энергии , меньшей
высоты барьера 0, должна иметь отрицательную кинетическую энергию 2 2 , ибо в классической механике
2
2

74 |
Уравнение Шрёдингера. Туннельный эффект |
[ Гл. 4 |
В нашем случае , а знaчит 2 2 0, что бесмыссленно, поскольку — действительная величина. Именно поэтому такие области и недоступны для классической частицы. Однако, согласно квантовой механике, частица может быть обнаружена в этой «запретной» зоне, т. е. квантовая механика как бы разрешает кинетической энергии быть отрицательной, а импульсу — мнимой величиной.
На самом деле последнее заключение неверно. Рассматривать полную энергию как сумму потенциальной и кинетической энергии можно только в классической механике, ведь это означает, что мы знаем одновременно импульс и координату частицы. Деление энергии на кинетическую и потенциальную в квантовой механике бесмыссленно, а потому и нет парадокса. Таков формальный ответ. Обнаружить частицу внутри барьера при
0 конечно можно. Однако при этом мы вносим по прин- ципу неопределенностей дополнительную дисперсию импульса
2 , и уже нельзя утверждать, что энергия частицы равна . Какова же она? Туннельный эффект (так называют в квантовой механике возможность «просачивания» частицы под барьером) заметен при 1, т. е. на таких расстояниях , что
2 |
2 0 |
1 |
(4.57) |
|
Тем самым мы должны фиксировать координату частицы с точностью , а при этом неизбежно появляется дисперсия импульса
|
2 |
|
2 |
|||
|
||||||
2 |
|
|
|
|||
|
|
|
|
4 2 |
|
|
|
4 2 |
|||||
Из соотношения (4.57) следует, что
22
8 0 ,
и значит
|
|
2 |
|
|
|
|
2 |
|
|
||
2 |
8 0 |
|
2 |
или |
|
, |
|||||
|
|
||||||||||
4 2 |
|
|
|||||||||
|
|
|
|
|
|
0 |
2 |
|
0 |
||
то есть изменение кинетической энергии частицы, вносимое при нашей попытке обнаружить частицу под барьером, больше той энергии, которой ей недостает до высоты барьера 0.
Прохождение частицы под потенциальным барьером называют туннельным переходом — название как бы означает, что «частица роет туннель под горой потенциального барьера».
Чтобы наши выводы стали понятнее, поясним, что понимается под термином «вероятность проникновения под барьером», который определяется выражением (4.56). В соответствии с вероятностным толкованием волновой функции это значит, что

4.3 ] Прямоугольный барьер. Туннельный эффект 75
если к барьеру слева подходит частиц с энергией (или скоростью 2 ), то в среднем лишь их доля (т. е. частиц) от полного числа пройдет через барьер, а доля 1 (т. е. 1 частиц) отразится от него и начнет двигаться налево.
Очевидно, что в силу экспоненциальной зависимости, туннельный эффект реален только для очень легких частиц на очень маленьких расстояниях.
Рассмотрим конкретный пример. Поместим на близком расстоянии друг от друга две металлические, например, железные, пластинки. Зависимость потенциальной энергии и атома, и электрона от координаты примерно соответствует прямоугольному барьеру. Высоту потенциального барьера для атома можно считать приблизительно равной той энергии, которую нужно затратить, чтобы оторвать его от кристалла, т. е. энергии сцепления
атома в кристалле. Для железа это 3,7 эВ. Пусть |
расстояние |
Æ |
10 7 см. |
между пластинками втрое больше атомного 10А |
Вероятность туннелирования атома железа (его масса Fe 56
1,6 10 |
24 9 10 23 г, а кинетическая |
энергия — порядка |
|||||||
тепловой Б 0,03 эВ, 0 3,7 эВ) будет |
|||||||||
|
|
|
2 10 |
7 |
|
|
|
|
|
|
|
2 9 10 23 3,7 1,6 10 |
12 |
||||||
|
|
|
|||||||
|
10 27 |
|
|||||||
2 1020 3,5 10 17 6000 10 2000
Таким образом, атом перейдет из одной пластинки в другую за время порядка 1 102000 109 лет, т. е. все время существования Вселенной слишком мал´о, чтобы можно было дождаться туннельного перехода хотя бы одного атома.
Ну а для электрона в той же ситуации? Его потенциал почти такой же (потенциал ионизации у железа равен 4,2 эВ), но масса — в 105 раз меньше. Для вероятности туннелирования сразу же получается увеличение в экспоненте в 105 300 раз, т. е. 10 10. Кажется, что и этого слишком мало. Проведем вычисления: число электронов в 1 см3 1023, их скорость3 107 см/с, следовательно за 1 с на 1 см2 поверхности на-
летает 1030 частиц, т. е. число протуннелировавших в 1 с будет
1020 cм 2. Это уже очень много. Если к тому же еще приложить напряжение 1 В, то можно получить токи порядка нескольких амперов. Но стоит щель увеличить вдвое — до
Æ
20 А — как 10 20, и ток упадет в 1010 раз.
Явление туннелирования «частицы» аналогично полному отражению от границы двух сред в оптике. Следует упомянуть,

76 |
Уравнение Шрёдингера. Туннельный эффект |
[ Гл. 4 |
что оптическое туннелирование наблюдал еще Ньютон. Он брал треугольную призму и прижимал к одной из ее граней сферическую линзу. Оказалось, что свет проходит не только в месте соприкосновения, а в небольшом кольце вокруг него.
Задачи
1.Найти плотность потока вероятности для плоской волны
и сферической волны 1 .
Решение. По определению комплексно-сопряженная волновая функция плоской волны , для сферической волны 1 . Поэтому для плоской волны по определению потока получается: 0 и
, где — скорость частицы, описываемой плоской
волной . В случае сферической расходящейся волны 1 вектор плотности потока направлен по радиусу-вектору r. Так как радиальная компонента вектора есть , то по определению потока получаем
|
1 |
|
, |
|||||
|
|
|
|
|
|
|||
2 2 |
||||||||
|
|
|||||||
или что то же самое: (так как ),
1
2 2
Тот же результат можно получить и в декартовых координатах:
|
|
|
|
|
|
1 |
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 2 |
||||||||||||||
1
2 2
Аналогично получаются выражения для и .
2. Найти коэффициент прозрачности прямоугольного потенциального барьера высоты 0 и ширины для частицы массы и энергии 0.
Решение. Фактически в задаче требуется получить формулу (4.55). Бу-
дем считать, что 0 при 0 и , и 0 при 0
(см. рис. 4.4). Пусть частица движется в положительном направлении оси
(т. е. из ). Тогда, согласно (4.51) и |
(4.52), волновая функция имеет |
|||
вид: в области 0, |
под барьером |
|||
(т. е. в области 0 ), и |
за барьером (при |
). Здесь |
||
|
|
|
|
|
2 2 и 2 0 2 . Сшивая волновые функции и их производные в точках 0 и , получаем систему уравнений относитель-
но , , и :
1 ,
1 ,
,
Решая эту систему, находим интересующий нас коэффициент (согласно (4.53) коэффициент прозрачности 2):
4
2 2

4.4 ] |
|
|
|
|
|
Задачи |
|
|
|
|
|
|
77 |
|||
Отсюда получаем, что коэффициент прозрачности |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
2 2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
4 2 2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если ширина барьера достаточно велика, а именно 1, то |
|
|
||||||||||||||
|
|
16 2 2 |
|
2 16 0 |
|
|
2 |
|
|
|
|
|||||
|
|
|
2 0 |
, |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||
2 2 2 |
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
|
|
|
|
|
|||||||
т. е. приходим к выражению (4.55) (с точностью до предэкспоненциального множителя).
3. При какой энергии электрон беспрепятственно пройдет над прямоугольным барьером высотой 0 5 эВ и шириной 0,1 нм?
Ответ: 0 2 2 2 2 2 5 37,62 2 эВ, где 1, 2, 3,
4. Электрон, находившийся в основном состоянии в одномерной прямоугольной потенциальной яме ширины 0,4 нм и глубины 0 10 эВ, переве-
ден в возбужденное состояние с энергией 10 2 эВ (нуль отсчета энергии — состояние покоя электрона вне ямы). Оценить время жизни возбужденного состояния, считая, что оно определяется вылетом электрона из ямы, а не переходом в основное состояние.
Решение. В соответствии с условиями задачи считаем, что потенциал0 при 0 и , и 0 при 0 . Вероятность вылета электрона в 1 с оценим как , где — частота ударов электрона о стенку, а — коэффициент прозрачности ступеньки высоты 0 для частицы с энергией . Как известно, 4 2, где 2 0 ,
2 — волновые числа электрона в яме и вне ее. Следовательно, 4 0 0 2 4 0 0 0,13;
2 0 2 5 1015 с 1. В результате 1 10 15 c. Следует, однако, иметь в виду, что приведеннная здесь оценка является оценкой по порядку величины, поскольку, как видно из полученного результата, электрон вылетает из ямы после 2–4 столкновений с краем ямы, а в этом случае используемый метод является весьма приближенным.
5. Волновая функция основного состояния частицы в одномерной бесконечно глубокой яме ширины имеет вид: 2 при 0
и 0 при 0 и . Найти средние значения координаты , ее квадрата, импульса и квадрата импульса частицы.
Решение. По правилу вычисления квантовомеханических средних имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 2 |
|
|
|
||||||||||||
|
|
|
|
|
|
; |
|
|
2 |
|
|
|
|
; |
|||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0; |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||
Теперь |
можно |
рассчитать |
2 |
2 |
и |
|
|
2 2 |
и сравнить |
их |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
произведение с тем, что следует из соотношение неопределенностей. Нетрудно получить, что
2 2 2

Г л а в а 5
ДИСКРЕТНОСТЬ ЭНЕРГЕТИЧЕСКИХ СОСТОЯНИЙ. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР. КУЛОНОВСКИЙ ПОТЕНЦИАЛ
5.1. Частица в потенциальной яме
Согласно классической физике финитное движение частицы происходит в ограниченной области пространства — потенциальной яме, определяемой физической природой взаимодействия частиц. Иными словами, потенциальная яма есть область, в которой на частицу действует сила, удерживающая ее в этой области. Термин «потенциальная яма» происходит от вида графика, изображающего зависимость потенциальной энергии частицы от координат, и применяется как в классической, так и в квантовой теории. Основное свойство потенциальной ямы — удерживать частицу, кинетическая энергия которой меньше глубины ямы; такая частица внутри потенциальной ямы будет находиться в связанном состоянии.
Связанное состояние — это состояние системы частиц, при котором их относительное движение происходит в ограниченной области пространства (т. е. является финитным) в течение длительного времени по сравнению с характерными для данной системы периодами. В природе существует огромное число связанных систем: от звездных скоплений и макроскопических тел до микрообъектов — молекул, атомов, ядер.
В классической механике частица с энергией, меньшей глубины потенциальной ямы, попав в нее, не сможет выйти и будет двигаться внутри ямы; положение частицы на дне ямы отвечает устойчивому равновесию и соответствует нулевой кинетической энергии. Если же энергия части-
1 |
2 |
цы превышает глубину потенци- |
|
||
|
|
альной ямы, то она преодолевает |
|
Рис. 5.1 |
действие сил притяжения и сво- |
|
|
бодно покидает яму. Примером |
может служить движение упругого шарика, находящегося в поле сил земного притяжения, в обычной яме с жесткими стенками (рис. 5.1). Шарик массы с энергией 1 не может покинуть

5.1 ] Частица в потенциальной яме 79
потенциальную яму глубиной , где — ускорение свободного падения, а — высота ямы (обычной), в которую попал шарик, и будет совершать колебания между точками 1 и 2 (если пренебречь трением), поднимаясь лишь до высоты 1 . Если же энергия шарика 2 , то он покинет яму и уйдет на бесконечность с постоянной скоростью , определяемой из
соотношения 2 2 |
2 |
. |
|
|
Вотличие от классической механики, в квантовой механике энергия, которой может обладать частица, находясь в потенциальной яме в связанном состоянии, принимает не непрерывные,
адискретные значения, т. е. существуют дискретные уровни энергии, причем наинизший (основной) уровень лежит выше дна ямы. Действительно, вследствие квантовомеханического соотношения неопределенностей между координатой и импульсом частицы локализация частицы 0 вблизи минимума потенциала приводит к большому значению ее средней кинетической энергии частицы (из-за большого разброса в значениях импульса . С другой стороны, уменьшение степени локализации 0 приводит к увеличению средней потенциальной энергии, так как частица проводит значительное время в области пространства, где потенциал превышает минимальное значение. Энергия основного состояния соответствует наименьшей возможной полной энергии квантовомеханической системы, совместимой с соотношением неопределенностей.
Впредыдущей главе уже упоминалось, что дискретность энергетических уровней микрочастицы, находящейся в какойлибо потенциальной яме, отчетливо проявляется в спектрах излучения и поглощения атомов, молекул, ядер. Ярким подтверждением дискретности атомных уровней являются эксперименты по возбуждению и ионизации атомов электронным ударом, впервые проведенные в 1913 г. Д. Франком и Г. Герцем (см. гл. 3). В этой главе мы рассмотрим ряд примеров стационарных состояний микрочастицы, находящейся во внешнем потенциальном поле.
Начнем наше рассмотрение с простейшей квантовомеханической задачи о частице массы в одномерном потенциальном «ящике» с бесконечными стенками и шириной (см. рис. 4.1).
Фактически, мы эту задачу уже решали, когда обсуждали в предыдущей главе движение электрона между двумя абсолютно отражающими стенками. Посмотрим, как ее решение получается непосредственно из уравнения Шрёдингера.
Стационарное уравнение Шрёдингера (4.23) в данном случае
имеет вид |
|
|
|
|
|
|
|||||
|
2 2 |
, или |
2 |
|
2 |
|
0 |
||||
|
|
|
|
|
|
|
|||||
2 2 |
2 2 |
||||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
(5.1) |
||

80 Дискретность энергетических состояний [ Гл. 5
Решением этого уравнения является функция
|
|
|
|
, где |
2 |
2 |
(5.2) |
||
|
|
|
|
|
|
||||
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
||
Физические условия на -функцию на границах 0, совершенно понятны — сквозь бесконечный потенциальный барьер частица не может даже протуннелировать, и, в силу непрерывности волновой функции, это приводит к условиям на границах потенциала
0, 0 |
(5.3) |
Значит, решение (5.2) уравнения (5.1) можно записать в виде
|
(5.4) |
со следующим из (5.3) и (5.4) условием . Последнее определяет возможные значения , а следовательно, и дискретные значения энергии , которые в силу связи и (см. (5.2)) равны
|
2 2 |
2 |
(5.5) |
2 |
, |
||
|
|
|
где 1, 2, 3
Случай 0 означает, что частицы нет вообще, т. е. этот случай решением не является. Напомним, что именно граничные условия определяют дискретность допустимых значений энергии частицы.
Константу найдем из условия нормировки -функции:
|
|
|
|
|
|
|
1 2 2 2 2 |
2 |
|||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
1 |
2 |
|
2 |
|
|
|
|
|
|
|
2 , (5.6) |
|
|
2 |
||||
|
|
0 |
|
|
|
|
откуда следует, что 2 и, таким образом, решение уравнения (5.1) имеет вид
|
2 |
|
|
|
|
(5.7) |
||
|
|
|
|
|||||
Здесь необходимо отметить, что в стационарном состояниине есть волновое число волны де Бройля, ибо -функция в данном случае не является плоской волной. Дело в том, что у частицы нет определенного импульса, имеется лишь распределение по , а в основном состоянии ( 1) вообще . В этом смысле , хотя строго определено. Это и есть проявление корпускулярно-волнового дуализма. Мы уже подчеркивали, что
