
студ ивт 22 материалы к курсу физики / belonuchkin_ve_zaikin_da_tsipeniuk_ium_kurs_obshchei_fiziki
.pdf
5.4 ] |
Задачи |
91 |
решения. Позже мы выясним, чему соответствуют решения, не обладающие сферической симметрией. Сейчас лишь отметим, что решение полной задачи не приводит к появлению новых уровней энергии.
Задачи
1. Потенциальную энергию взаимодействия атома гелия с плоской поверхностью твердого тела можно аппроксимировать прямоугольной ямой типа (5.12) ширины 0,5 нм. Полагая, что волновая функция адсорбированного атома в основном состоянии достигает максимума при 0,99 , определить среднее значение координаты для адсорбированных атомов в основном состоянии.
Решение. Внутри ямы (0 ) волновая функция , а вне ее ( ) — . Условие сшивания при дает. Так как максимум достигается при 1 0,99 , то 1 2 , или2 1 Æ , где Æ 0,01. Тогда условие сшивания можно переписать в виде
|
2 Æ2 |
Æ |
|
|
|
, т. е. |
|
Æ |
2 |
Æ |
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
2 Æ2 2 |
|
2 |
2 |
|
||||||||
|
|
|
|
|
|||||||||
Отсюда видно, что 1 , поэтому плотность вероятности нахожде- |
|||||||||||||
ния атома вне ямы 2 2 |
заметно убывает на расстоя- |
||||||||||||
ниях, значительно больших |
, и |
с хорошей |
точностью |
можно |
|
положить |
|||||||
1 2 10 нм.
2.Частица массы находится в одномерной прямоугольной яме с абсолютно непроницаемыми стенками (0 ). Найти вероятность нахождения частицы с наименьшей энергией в области 3 2 3 и число энергетических уровней в интервале , .
Ответ: |
1 |
|
3 |
|
0,61; |
|
|
|
|
|
. |
3 |
2 |
|
2 |
|
|||||||
|
|
|
|
|
|
||||||
3.Показать, что в основном состоянии гармонического осциллятора
2, где и — среднеквадратичные отклонения импульса и координаты от их средних. Волновая функция этого состояния имеет вид 0
4 2 2 , где .
Решение. Легко убедиться, что для рассматриваемого состояния и
равны нулю. Поэтому 2 2 и 2 2. Находя 2 и 2 по правилу вычисления квантовомеханических средних (имея в виду, что , а ), получаем
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
2 |
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
||||||||||||||||
2 |
|
, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
2 2 |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
1 |
|
|
|
||||||||
|
|
|
|
2 |
, |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 2 |
или |
2 |
2 |
|
|
||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||
4. В угарном газе CO из-за возбуждения колебаний молекул наблюдается пик поглощения инфракрасного излучения на длине волны 4,61 мкм. Опре-

92 Дискретность энергетических состояний [ Гл. 5
делить амплитуду 0 нулевых колебаний молекул CO. Оценить температуру, при которой амплитуда тепловых колебаний превзойдет 0 .
Решение. Для осциллятора кин пот 2, т. е. в основном состоянии
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
2 |
|
|
|||
|
0 |
|
0 |
, |
2 |
, |
|
|
, |
|
|||||||||
|
2 |
4 |
|
2 |
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
11,3 10 |
24 г, |
0 |
|
|
3,3 10 10 |
см |
||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Амплитуда тепловых колебаний превзойдет 0, когда средняя энергия теплового движения, приходящаяся на одну степень свободы, станет больше энергии
нулевых колебаний, т. е. Б , или 3000 K.
5. Позитроний представляет собой связанную систему из электрона и позитрона, вращающихся вокруг центра масс этой системы. Найти уровни энергии позитрония.
Решение. Отличие позитрония от водорода сказывается только в приведенной массе: для водорода H , а для позитронияп 2, так как массы электрона и позитрона равны.
Отсюда следует, что уровни энергии позитрония по абсолютной величине практически в два раза меньше уровней энергии водорода для одних и тех же значений квантового числа , т. е.
4
2 2 12 4 4 0

Г л а в а 6
ПРОСТРАНСТВЕННОЕ КВАНТОВАНИЕ. СПИН ЭЛЕКТРОНА
6.1. Пространственное квантование
Энергия физической системы в зависимости от формы потенциальной кривой может иметь либо непрерывный, либо дискретный спектр. В то же время другая физическая величина — момент импульса — для любой системы может принимать только определенный, дискретный ряд значений. Момент импульса характеризует вращательное (угловое) движение. При изучении такого движения удобно пользоваться полярной системой координат (рис. 6.1). В этой системе положение точки характеризуется расстоянием от начала отсчета, полярным углом между полярной осью
и радиусом-вектором r и азимутальным углом , отсчитываемым в плоскости от оси .
Волновая функция , описыва- |
|
|
ющая состояние с определенным зна- |
|
|
чением проекции на ось ана- |
|
|
логична плоской волне де Бройля |
|
|
: роль координаты игра- |
Рис. 6.1 |
|
ет азимутальный угол (угол поворо- |
||
|
та вокруг оси ), а роль проекции импульса — проекция момента импульса на эту ось; оператор проекции момента импульса имеет
вид: , и, таким образом, |
|
|
(6.1) |
При этом по смыслу угловой переменной углы и 2 описывают одно и то же положение частицы относительно оси : если систему повернуть вокруг оси на угол 2 , то она перейдет сама в себя. Поэтому волновые функции должны удовлетворять условию периодичности
2 |
(6.2) |
Как следует из (6.1), это условие выполняется лишь |
в том |

94 |
Пространственное квантование. Спин электрона |
[ Гл. 6 |
случае, если принимает целочисленные значения. Следовательно, , в отличие от проекции импульса , может принимать только дискретные значения:
, |
где |
0, 1, 2, |
(6.3) |
Таким образом, проекция момента импульса на любую ось |
|||
квантуется и равна |
целому |
числу постоянных Планка |
(на |
рис. 6.2 дано схематическое изображение квантования проекции
|
момента импульса L на ось ). |
|
|
Квантование проекции момента озна- |
|
|
чает, что вектор квантового момента им- |
|
|
пульса не может иметь произвольного на- |
|
|
правления по отношению к любому фик- |
|
|
сированному направлению в простран- |
|
|
стве. Этот факт получил название про- |
|
|
странственного квантования. Оно вы- |
|
|
глядит крайне необычно: поскольку на- |
|
|
правление оси можно выбрать произ- |
|
|
вольно, то проекции момента на два раз- |
|
|
личных направления ( и ) квантуются |
|
|
одинаково. Возможные значения проекции |
|
Рис. 6.2 |
момента на оси и также определяются |
|
формулой (6.3). |
||
|
Может показаться, что квантование проекции приводит к тому, что вектор составляет лишь определенные углы с осью, как это схематично показано на рис. 6.2. Однако полученный результат имеет совсем другой смысл. Формула (6.3) показывает, что при измерении проекции момента импульса мы в результате опыта обязательно получим число, являющееся кратным . Однако значение до этого вовсе не должно быть равно целому числу . До и после опыта -функции вовсе не обязаны совпадать. Мы вправе лишь утверждать, что -функция состояния, имевшегося до опыта, т. е. -функция любого физического состояния, может быть представлена в виде суперпозиции собственных решений:
|
|
|
1 |
|
, |
(6.4) |
||
|
|
|
||||||
|
|
|
2 |
|
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
где множитель 1 2 |
возникает |
как |
результат |
нормировки |
||||
функций . |
|
|
|
|
|
|
|
|
Система, описываемая такой -функцией, не обладает определенной проекцией момента L. Вектор L может быть направлен произвольным образом, но при измерении всегда будет найдено какое-то одно из значений, входящих в сумму (6.4). Вероятность найти значение определяется, как всегда, величиной 2.

6.1 ] Пространственное квантование 95
Таким образом, вектор момента импульса не имеет определенного направления в пространстве. В этом смысле рис. 6.2 является условным. При фиксированном значении проекции момента на ось вектор момента импульса как бы прецессирует вокруг этой оси, из-за чего проекции и не имеют определенных значений (рис. 6.3). В данном случае мы снова сталкиваемся с действием квантовомеханического принципа неопределенностей.
Проекция момента не может быть больше |
|
|
его абсолютного значения. Поэтому при фик- |
|
|
сированной величине модуля момента воз- |
|
|
можные значения числа ограничены свер- |
|
|
ху числом . Если задано, то проекция |
|
|
момента может принимать 2 1 значений. |
|
|
Найдем возможные значения момента им- |
|
|
пульса. Средние значения проекций , |
|
|
и , как и любых других величин, могут |
|
|
иметь в данном состоянии определенные зна- |
|
|
чения. Если никаких предварительных опе- |
Рис. 6.3 |
|
раций для фиксации проекции момента на |
||
|
какое-либо направление не производилось (нет выделенной поляризации частиц), то все направления равноправны и средние значения квадратов проекций момента импульса одинаковы:
2 2 2 |
(6.5) |
||
|
|
|
|
Это утверждение вместе с правилом квантования проекции момента (6.3) позволяет определить возможные значения квадрата момента импульса.
Среднее значение квадрата момента, как и в классической механике, равно сумме средних значений квадратов проекций. Учитывая равенство (6.5), получим
2 2 2 2 3 2 |
(6.6) |
|||
|
|
|
|
|
При любой ориентации момента его квадрат имеет одну и ту же величину. Следовательно,
2 2 3 2 |
(6.7) |
|
|
Все значения равновероятны, если никакого отбора по возможным состояниям не производилось. Поэтому среднее значение 2 равно сумме всех 2 1 возможных значений 2 отдо , деленной на их полное число:
|
|
2 |
1 2 2 |
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|||||
|
2 |
2 |
|
|
|
|
|
|
|
12 |
|
22 |
|
32 |
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 1 |
|
|
2 1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 2 |
|
1 2 1 |
|
2 |
1 |
|||||||||
|
|
|
|
2 1 |
|
3 |
||||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|||||

96 Пространственное квантование. Спин электрона [ Гл. 6
Здесь мы использовали известное выражение для суммы квадра-
тов целых чисел от 1 до . Подставив полученное значение |
2 |
|
|
в (6.6), найдем |
|
2 2 1 |
(6.8) |
Равенство (6.8) определяет закон квантования квадрата момента импульса, т. е. его длину.
Число , от которого зависят значения проекции момента, называется магнитным квантовым числом. Этот термин обусловлен тем, что, как мы увидим в дальнейшем, проекция магнитного момента, создаваемого движением заряженной частицы, пропорциональна проекции момента импульса этой частицы, определяемого числом . Максимальное значение магнитного квантового числа , а минимальное . Число , определяющее возможные значения квадрата момента, называется орбитальным квантовым числом.
Отметим еще одно отличие квантового момента от классического. Максимальное значение проекции квантового момента
не равно модулю момента 1 , а меньше его. Мы уже подчеркивали, что в силу соотношения неопределенностей у микрочастицы не могут быть одновременно известны проекции момента на две различные оси. Зафиксировав состояние с определенным , мы вносим неопределенность в проекции и .
В квантовой механике задание 2 и одной из проекций момента импульса полностью определяет вращательное состояние тела.
6.2. Состояния атомных электронов с разными моментами импульса
Зная закон квантования момента импульса, мы можем теперь полностью классифицировать состояние электрона в атоме. Действительно, электрон в атоме может обладать и ненулевым моментом импульса l, таким, что
2 2 1 , |
0, 1, 2, 3, , |
(6.9) |
а его проекция на заданную ось принимает при этом значения
, 0, 1, 2, 3, , |
(6.10) |
Как уже упоминалось, вектор l принято называть орбитальным моментом импульса, — орбитальным квантовым числом, а— магнитным квантовым числом (оно определяет возможные значения проекции орбитального момента l на какую-либо ось). Отметим, что при обозначении индекс « » часто опускают, однако мы вводим его, чтобы не путать магнитное квантовое число с массой электрона.

6.2 ] Состояния атомных электронов с разными моментами импульса 97
Исторически (это пришло из оптики) состояния с различными имеют соответственно следующие наименования:
0 называется -состоянием (от английского слова sharp),
1 называется -состоянием (от английского слова prin-
cipal),
2 называется -состоянием (от английского слова dif-
fuse), и так далее по алфавиту (f, g, h, ...).
Раньше мы искали стационарное состояние атома водорода, предполагая, что решение является сферически-симметричным, т. е. зависит только от радиуса, но не от угловых переменных. Теперь снимем это ограничение. Представим -функцию в виде произведения угловой и радиальной компонент (что, оказывается, возможно):
, , , |
(6.11) |
В механике доказывается, что кинетическая энергия тела, движущегося в поле центральных сил, может быть представлена как сумма кинетических энергий радиального и вращательного
движений, т. е. |
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
, |
(6.12) |
|
|
|
|
|
2 2 |
|||||
|
2 |
2 |
|
|
|
|||||
где момент импульса является интегралом движения (сохраняющейся величиной) в центральном поле. Поэтому, если у тела есть ненулевой угловой момент, то эффективную потенциальную энергию радиального движения удобно представить в виде
эф |
2 |
|
2 1 |
, |
(6.13) |
2 2 |
2 2 |
||||
где — обычная потенциальная энергия (в атоме — энергия кулоновского взаимодействия). Таким образом, формально уравнение Шрёдингера имеет такой же вид, как и в радиальносимметричном поле, но с другим потенциалом (к кулоновскому потенциалу теперь добавляется центробежный).
Поскольку величина момента импульса тела, находящегося в поле центральных сил, сохраняется, то волновые функции частицы в таком поле являются собственными функциями оператора квадрата момента импульса:
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 2 1 , |
|
(6.14) |
||||
а уравнение Шрёдингера имеет следующий вид: |
|
|
|||||||
|
2 |
|
|
|
|
2 1 |
|
0 |
(6.15) |
|
2 |
2 2 |
|
||||||
|
|
|
|
|
|
||||
Радиальная волновая функция квантуется так же, как и-функция симметричного состояния ( -состояние). Обозначим
4 Основы физики. Т. II
98 |
Пространственное квантование. Спин электрона |
[ Гл. 6 |
соответствующие радиальные квантовые числа через . Согласно вычислениям в чисто кулоновском поле энергия электрона зависит только от квантового числа , такого что ,
1, 2, 3, , 0, 1, 2, 3,
Поэтому
1, 2, 3, |
(6.16) |
Это число называется главным квантовым числом.
Отметим, что радиальное квантовое число однозначно связано с числом узлов радиальной волновой функции (т. е. точек, в которых эта функция обращается в нуль) внутри области, в которой эта функция определена, а именно: число таких узлов равно 1. Как нетрудно убедиться, квантовое число состояний частицы в бесконечно глубокой прямоугольной потенциальной яме (§ 5.1) точно так же связано с числом узлов соответствующей волновой функции внутри интервала ее определения.
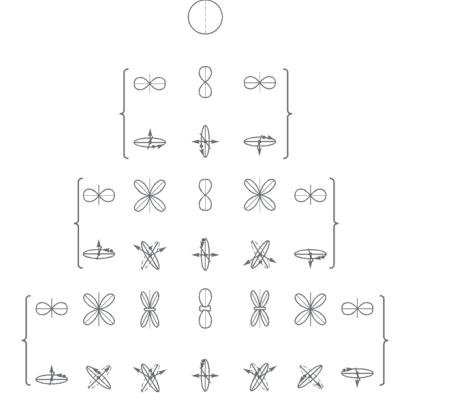
На рис. 6.4 показаны угловые распределения плотности -,- и -электронов в атоме при различных значениях магнитного
|
|
l = 0 |
|
s- |
|
|
|
|
|
|
|
электроны |
|
|
|
|
|
|
m = 0 |
|
|
|
|
|
|
z |
|
z |
|
|
|
|
l = 1 |
m = 1 |
m = 0 |
m = |
p- |
|
|
|
электроны |
|
|||||
|
|
|
|
|
|
||
|
z |
|
|
z |
z |
|
|
|
|
|
|
|
|
|
|
l = 2 m = 2 |
m = 1 |
m = 0 |
m = m = 2 |
d- |
|
||
|
|
|
|
|
|
электроны |
|
z |
z |
|
|
|
z |
z |
|
l = 3 m = 3 m = 2 |
m = 1 |
m = 0 |
m = m = 2 m = 3 |
f- |
|||
|
|
|
|
|
|
|
|
электроны
Рис. 6.4

6.2 ] Состояния атомных электронов с разными моментами импульса 99
квантового числа . Одновременно показано, какому движению электрона такие состояния соответствуют в боровской модели атома.
Распределение по углам обладает симметрией тела вращения около той оси, на которую фиксирована проекция момента импульса (на рисунке это ось ). При 0 электрон может находиться лишь в -состоянии, которому соответствует полная шаровая симметрия. Следует заметить, что в модели атома Бора такого состояния просто нет. При 1 cимметрия состояния соответствует симметрии типа диполя, при 2 возможна и симметрия типа квадруполя, когда максимум вероятности нахождения электрона соответствует углу 4.
Распределение заряда по радиусу определяется радиальной волновой функцией . Так, для сферически симметричных состояний заряд сферического слоя радиуса и толщины равен
4 2 2 |
(6.17) |
У -состояния волновая функция максимальна в нуле, а с ростом радиального квантового числа максимум ее смещается все дальше от центра (рис. 6.5). Поскольку распределение заряда определяется согласно формуле (6.17) произведением2 2 , то его максимум всегда смещен от центра атома, но чем больше радиальное квантовое число, тем больше это смещение, то есть, грубо говоря, тем дальше расположен электрон от ядра.
Обратим еще раз внимание на следующий факт: в теории Бора электроны движутся по плоским орбитам, т. е. они не могут быть сферически симметричными. Согласно этой теории нулевым моментом импульса обладал бы элек-
трон, движущийся прямолинейно вдоль радиуса, но тогда по классическим законам он бы натолкнулся на ядро. В квантовой механике, в которой нет представления о движении электронов по орбитам, нет и никаких препятствий для реализации сферически симметричных состояний атома. Поэтому волновая функция электрона в атоме может быть сферически симметричной, т. е.
4*

100 |
Пространственное квантование. Спин электрона |
[ Гл. 6 |
зависит только от радиуса. В таком случае, как мы уже говорили, энергия определяется выражением
|
2 4 |
2 |
(6.18) |
|
|
2 2 |
|||
|
2 4 0 |
|
|
|
На рис. 6.6 показано распределение электронной плотности по радиусу в боровской модели и при квантовомеханическом описании. Как указывалось выше, радиальная волновая функция имеет число узлов, на единицу меньшее, чем номер соответствующего стационарного состояния. Это хорошо
видно из рис. 6.5.
Итак, при заданной энергии (данном значении ) возможны состояния со всеми , удовлетворяющими условию 0 1, а всего квантовое число может принимать
Рис. 6.6 |
различных значений. Однако при данном |
|
электрон может находиться в 2 1 состояниях с различными значениями квантового числа . Таким образом, нетрудно рассчитать число различных состояний, соответствующих одной и той же энергии, и оно равно
1 |
1 2 1 |
2 |
|
||
2 1 |
(6.19) |
||||
2 |
|
||||
0
В этом случае говорят, что уровень вырожден, а число состояний, соответствующих одной и той же энергии, определяет кратность вырождения. В нашем случае получается 2-кратное вырождение. Несколько забегая вперед, отметим, что для стационарных состояний электрона в кулоновском поле имеет место еще дополнительное двукратное вырождение, связанное со спином электрона, так что на самом деле в кулоновском поле электронный уровень оказывается 2 2-кратно вырожденным.
Обратимся теперь к вопросу о магнитном квантовом числе . Если заряженная частица (в нашем случае — электрон) обладает ненулевым моментом импульса, то это означает, что в системе имеются токи, следовательно, система должна обладать и магнитным моментом.
Рассмотрим классическую задачу о магнитном моменте электрона, движущегося по окружности (рис. 6.7). С движением заря-
женной частицы массой со скоростью по окружности радиуса связаны как механический момент L, так и магнитный .
