Часть 1 Волновая оптика
1 Волновая теория света
1.1 Электромагнитные волны
Электромагнитным
полем называется поле, которое состоит
из электрического и магнитного полей,
существующих одновременно в одних и
тех же точках пространства, в одни и те
же моменты времени. Электромагнитное
поле в любой момент времени t
определяется заданием в каждой точке,
определяемой радиус-вектором
двух векторов: напряженности электрического
поля
и индукции
магнитного
поля.
Источниками
электромагнитного поля являются заряды
и токи, для характеристики которых
вводят объемную плотность заряда
и вектор плотности тока
.
Связь электрического и магнитного полей
выражается системой уравнений Максвелла.
Эти уравнения являются своего рода
аксиомами электродинамики, полученными
путем обобщения опытных фактов и
экспериментальных сведений о свойствах
электрических и магнитных полей.
Уравнения Максвелла могут быть записаны в интегральной и дифференциальной формах. Интегральная форма записи уравнений устанавливает связь между величинами в разных точках поля или на разных отрезках, поверхностях. Дифференциальная форма описывает соотношение между величинами вблизи одной и той же точки поля в определенный момент времени. Эту форму записи применяют при исследовании полей, изменяющихся от точки к точке.
1. Закон электромагнитной
индукции Фарадея: переменное во времени
магнитное поле порождает электрическое
поле, направление которого связано с
направлением
,
и определяется правилом левого винта
;
. (1.1.1)
2. Закон полного
тока: электрический ток и изменяющееся
во времени электрическое поле порождают
магнитное поле. Направление вектора
напряженности магнитного поля
связано с направлением полного тока и
определяется правилом правого винта.
;
. (1.1.2)
3. Обобщенная теорема Остроградского-Гаусса: поток вектора электрического смещения через замкнутую поверхность равен алгебраической сумме свободных зарядов, находящихся внутри объема, ограниченного этой поверхностью.
;
. (1.1.3)
4. Теорема Остроградского-Гаусса для магнитных полей: магнитный поток через замкнутую поверхность равен нулю. Магнитные силовые линии замкнуты и не имеют ни истоков, ни стоков.
;
. (1.1.4)
Уравнения
и
устанавливают взаимосвязь вектора
электрического смещения с вектором
напряженности электрического поля и
вектора магнитной индукции с вектором
напряженности магнитного поля.
Из уравнений
Максвелла следует возможность
существования связанных между собой
во времени и пространстве вихревых
электрических и магнитных полей даже
при отсутствии зарядов и токов, т.е. при
,
.
Такие поля представляют собой
электромагнитные волны. Уравнения
Максвелла в дифференциальной форме для
электромагнитной волны, распространяющейся
в однородной ( = const,
= const)
и непроводящей среде, выглядят следующим
образом:
(1.1.5)
1.2 Операторная запись уравнений Максвелла
Для удобства написания приведенных ранее формул введем векторный дифференциальный оператор Гамильтона (). В декартовой системе координат этот оператор записывается следующим образом:
, (1.2.1)
где
,
и
– орты соответствующих координатных
осей.
При помощи этого оператора выражения для градиента некоторой скалярной величины можно записать в виде:
.
Для заданного в
некоторой области пространства векторного
поля
операторы дивергенции и ротора
записываются в виде:
и
.
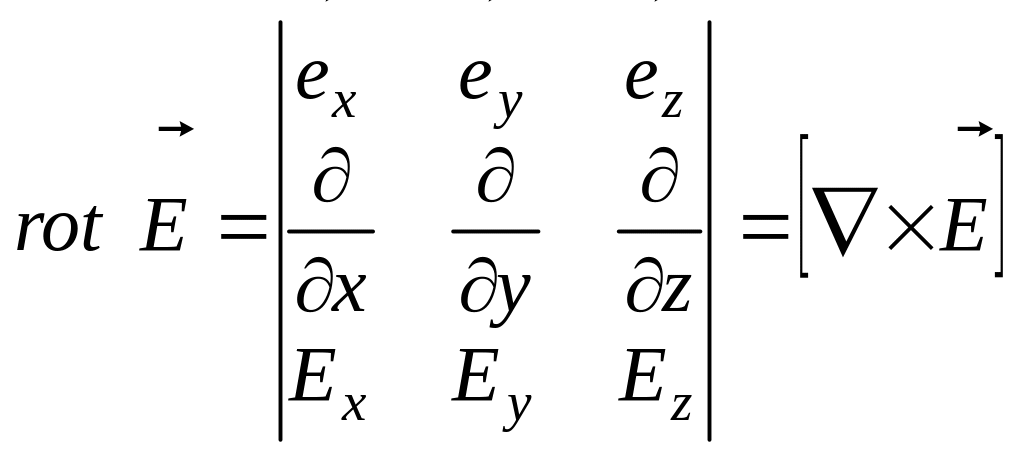По сути действие оператора Гамильтона эквивалентно различным способам дифференцирования. В физике наряду с оператором Гамильтона часто используют оператор двойного дифференцирования – оператор Лапласа (). Действие оператора Лапласа на скалярную величину можно определить как скалярное произведение оператора Гамильтона на градиент .
,
(1.2.2)
Действие оператора Лапласа на вектор определяет двойное действие гамильтониана по следующей формуле:
. (1.2.3)
Уравнения Максвелла
в дифференциальной форме (с учетом
,
)
можно записать так:
(1.2.4)
1.3 Волновое уравнение и уравнение электромагнитной волны
Распространение электромагнитного поля в пространстве – это волновой процесс, который может быть описан волновыми уравнениями. Рассмотрим вывод волновых уравнений из уравнений Максвелла для однородной, изотропной, непроводящей среды. Продифференцируем второе уравнение системы (1.2.4) по времени. С учетом того, что дифференцирования по времени и координатам являются независимыми друг от друга операциями, их можно поменять местами, т.е.
.
С другой стороны,
из первого уравнения, с учетом связи
векторов
и
,
,
тогда
.
Или с учетом связи
векторов
и
,
. (1.3.1)
Распишем левую часть уравнения (1.3.1) так, как это сделано в формуле (1.2.3). С учетом третьего уравнения системы (1.2.4) получаем
или
. (1.3.2)
Уравнение (1.3.2) представляет собой волновое уравнение для электрической составляющей электромагнитной волны. Проводя аналогичные математические преобразования, можно получить волновое уравнение и для магнитной составляющей
. (1.3.3)
Данные уравнения являются уравнениями электромагнитной волны, распространяющейся в веществе с диэлектрической проницаемостью и магнитной проницаемостью со скоростью
.
(1.3.4)
Заметим, что электромагнитная волна распространяется в вакууме с постоянной скоростью
.
Следовательно, уравнение (1.2.4) можно записать в виде
.
(1.3.5)
Решением волновых уравнений (1.3.2) и (1.3.3) являются волновые функции
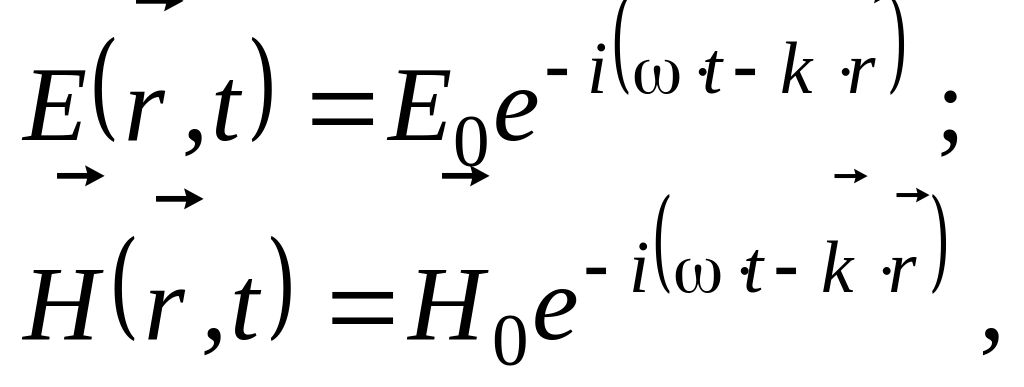(1.3.6)
где i
– мнимая единица;
– частота колебаний;
– вектор, в направлении которого
распространяются колебания;
и
– постоянные по модулю векторы, не
зависящие от координат и времени.
Координаты векторов
и
могут
быть комплексными числами, то есть иметь
действительную и мнимую часть.
Действительная часть уравнений (1.3.6)
имеет вид
(1.3.7)