3530

2 . Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т. е.

kf (x)dx k f (x)dx.

4 . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности, т. е.

f (x) g(x) dx f (x) dx g(x) dx.

2.3. Таблица основных интегралов

Приведем таблицу основных интегралов. Часть формул этой таблицы непосредственно следует из определения интегрирования как операции, обратной дифференцированию, и таблицы производных.

Справедливость остальных формул легко проверить дифференцированием.

50

Интегралы, содержащиеся в этой таблице, принято называть табличными.

2.4.Основные методы интегрирования

1.Непосредственное интегрирование. Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием.

Пример 1.

51

2. Метод подстановки. Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла, т.е. перейти к непосредственному интегрированию.

Такой метод называется методом подстановки или методом

множество значений этой функции, на котором определена

52

Возвращаясь к переменной х, окончательно получаем

З а м е ч а н и е. При замене переменной в неопределенном интеграле иногда более удобно задавать не х как функцию t, а, наоборот, задавать t как функцию от х.

Заметим, что удачный выбор подстановки обычно представляет известные трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.

53

3. Метод интегрирования по частям. Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.

Теорема 3. Пусть функции u(x) и v(x) определены и дифференцируемы на некотором промежутке Х и пусть функция u (x) v(x) имеет первообразную на этом промежутке. Тогда на промежутке Х функция u(x) v (x) также имеет первообразную и справедлива формула

u(x) v (x)dx u(x) v(x) v(x) u (x)dx. (2.2)

54

Формула (2.2) называется формулой интегрирования по

55

называются элементарными множителями. Если среди них

где r, s,… t – целые числа, которые называются соответственно

кратностями корней , , , причем r s t n, n

степень многочлена Q(x).

Среди корней представления (2.4) могут быть и комплексные. В алгебре доказывается, что если 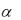a bi r - кратный комплексный корень многочлена с действительными коэффициентами, то этот многочлен имеет также сопряженный

57

где p a, q a2 b2 , p2 q 0, p и q – действительные числа.

Поступая аналогично с остальными комплексными

В высшей алгебре доказывается следующая теорема.

R(x)

Теорема 4. Если рациональная функция имеет

Q(x)

степень многочлена в числителе меньше степени многочлена в знаменателе, а многочлен Q(x) представлен в виде (2.5), то эту функцию можно единственным образом представить в виде

действительные числа.

Выражение (2.6) называется разложением рациональной функции на элементарные дроби. Оно имеет место для всех х,

не являющихся действительными корнями многочлена Q(x). Чтобы определить числа

A1, A2 , , Ar , , M1, N1, , M t , Nt , , умножим обе части разложения (2.6) с неизвестными пока A1, A2 , на Q(x).

Поскольку равенство между многочленом R(x) и многочленом, который получится в правой части, должно быть справедливо для всех х, то коэффициенты, стоящие при равных степенях х, должны быть равны между собой. Приравнивая их, получаем

58

систему уравнений первой степени, из которой найдем неизвестные числа A1, A2 , , Ar , , M1, N1, , M t , Nt , Такой метод отыскания коэффициентов разложения рациональной