
3530
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i dx jdy kdz , |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||
dr |
|
i |
|
|
|
j |
|
k |
|
|
||||||||||||
|
|
x |
y |
z |
||||||||||||||||||
а соответствующие выражения для полного приращения дифференцируемой функции и ее полного дифференциала записываются в форме
du(M ) |
|
|
|
|
u |
|
|
|
u |
|
|
u |
|
)dz , |
|||
|
|
|
|
|
|
|
|
||||||||||
|
u(M ) dr |
|
|
(M |
0 |
)dx |
|
|
(M |
0 |
)dy |
|
(M |
0 |
|||
|
|
|
|
|
|||||||||||||
0 |
0 |
|
|
x |
|
|
y |
|
z |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
u |
du(M 0 ) 0( |
) . |
|
|
|
|
(4.32) |
||||||||
В двумерном случае (когда рассматриваем функции двух переменных)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
i dx jdy , |
|
i |
|
|
j |
|
|
, |
|
|
|||||||||||
|
|
x |
|
y |
||||||||||||||||||||
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
u(M 0 ) dr |
0( ) , |
|
du(M 0) |
|
|
|
|
|
u(M 0) dr . |
||||||||||||||
З а м е ч а н и е 2 . Теоремы 1 и 2 выражают лишь необходимые условия дифференцируемости функции в точке: как непрерывность функции f (x, y) , так и существование у нее
обеих частных производных в точке вытекают из дифференцируемости в этой точке. Если хотя бы одно из этих условий не выполняется в какой – либо точке, то функция не может быть дифференцируема в этой точке.
Обратные утверждения к теоремам 1 и 2 неверны. Из непрерывности функции в точке, а также из существования ее частных производных в этой точке, еще не следует дифференцируемость функции. Для практических целей требуются достаточные критерии дифференцируемости функции.
Оказывается, что в отличие от функции одной переменной, для дифференцируемости функций многих переменных достаточно непрерывности частных производных в точке.
200

3. *) Достаточные условия дифференцируемости.
Теорема 3. Если функция u  f (x, y) имеет частные производные по всем аргументам в точке M 0 (x0 , y0 ) и в некоторой окрестности этой точки, причем все эти частные
f (x, y) имеет частные производные по всем аргументам в точке M 0 (x0 , y0 ) и в некоторой окрестности этой точки, причем все эти частные
производные в точке M 0 непрерывны, то функция u |
f (x, y) |
||||||||
дифференцируема в точке M 0 (x0 , y0 ) . |
|
|
|
||||||
Доказательство. Пусть частные производные |
f x (x, y) и |
||||||||
f y (x, y) |
существуют для всех точек M (x, y) , принадлежащих |
||||||||
окрестности точки M 0 (x0 , y0 ) . |
|
|
|
|
|
||||
Пусть они непрерывны в точке |
M 0 (x0 , y0 ) . Обозначим |
||||||||
x x0 |
x , y |
y0 |
y . Тогда полное приращение функции в |
||||||
точке M 0 (x0 , y0 ) можно записать в следующем виде |
|
|
|||||||
|
u |
f (x0 |
x, y0 |
y) |
f (x0 , y0 |
y) |
|
|
|
|
|
|
f (x0 , y0 |
y) |
f (x0 , y0 ) . |
|
(4.33) |
||
Выражение в первой скобке равенства (4.33) является |
|||||||||
приращением функции f (x, y0 |
y) |
одной переменной х на |
|||||||
сегменте |
x0 , x0 |
x . По условию теоремы |
функция |
||||||
u f (x, y) |
имеет |
частные |
производные. |
Поэтому |
|||||
рассматриваемая функция |
одной |
переменной |
f (x, y0 |
y) |
|||||
дифференцируема и ее производная по х является в то же время
частной |
производной f x функции |
f (x, y) . Применяя |
к |
|||
приращению |
функции f (x, y0 |
y) |
теорему Лагранжа |
о |
||
конечном приращении, получим |
|
|
|
|
||
f (x0 |
x, y0 |
y) f (x0 , y0 |
y) f x (x0 1 x, y0 |
y) |
x, |
|
(4.34)
______________________________________________________
*) Материал этой части предназначен для самостоятельного изучения.
201

где 0 |
1 |
1, |
так что x0 |
1 x |
- |
некоторая точка интервала |
|||||||
(x0 , x0 |
x) . |
|
|
|
|
|
|
|
|
|
|
||
|
Вторая скобка в (4.33) представляет собой приращение |
||||||||||||
функции f (x0 , y) |
на сегменте |
|
y0 , y0 |
y . |
Рассуждения, |
||||||||
совершенно аналогичные предыдущим, позволяют записать |
|||||||||||||
|
|
f (x0 , y0 |
y) |
f (x0 , y0 ) |
f y (x0 , y0 |
2 |
y) |
y , |
(4.35) |
||||
0 |
2 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
производные |
f x |
и |
f y |
непрерывны в |
точке |
||||||
M 0 (x0 , y0 ) |
по условию теоремы, то при |
x |
0, y |
0 |
|
||||||||
|
|
|
f x (x0 |
1 x, y0 |
y) |
f x (x0 , y0 ) , |
|
|
|||||
|
|
|
|
f y (x0 , y0 |
2 y) |
|
f y (x0 , y0 ) . |
|
|
|
|||
|
Но это значит (по определению предела), что в |
||||||||||||
достаточно |
малой |
окрестности |
точки |
M 0 |
эти |
величины |
|||||||
отличаются на бесконечно малые. Таким образом, можно записать равенства:
|
f x (x0 |
1 x, y0 |
y) |
f x (x0 , y0 ) |
( x, y) , |
|
||
|
f y (x0 , y0 |
2 y) |
|
f y (x0 , y0 ) |
( x, y) , |
(4.36) |
||
где |
0, |
0 при |
x |
0, |
y |
0. |
|
|
Учитывая выражения (4.34) – (4.36), полное приращение функции u 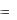 f (x, y) (4.33) можно записать в виде
f (x, y) (4.33) можно записать в виде
u f x (x0 , y0 ) x f y (x0 , y0 ) y |
x |
y , |
|||
совпадающем с |
выражением |
u (4.18). |
Следовательно, |
||
функция u |
f (x, y) дифференцируема в точке M 0 . |
|
|||
Следствие. |
Если функция |
f (x, y) |
имеет |
в точке |
|
M 0 (x0 , y0 ) |
и ее окрестности частные производные |
f x (x, y) , |
|||
202

f y (x, y) , причем эти частные производны непрерывны в точке
M 0 , то функция f (x, y) также непрерывна в этой точке. Действительно, поскольку частные производные
существуют в окрестности точки M 0 , в самой этой точке, и непрерывны в точке M 0 , то функция по теореме 3 дифференцируема в точке M 0 (x0 , y0 ) . Но поскольку функция дифференцируема в точке M 0 (x0 , y0 ) , то, согласно теореме 1,
она непрерывна в этой точке.
Установленная теорема 3 имеет важное значение для практической проверки дифференцируемости функции. Дело в том, что непосредственная проверка дифференцируемости с помощью определения (4.18), (4.20) или (4.22) часто весьма затруднительна. Проверка же непрерывности частных производных оказывается проще. Но не следует забывать, что непрерывность частных производных – это достаточное условие. Если производные не являются непрерывными функциями, то не следует думать, что функция обязана быть недифференцируемой!
В заключение отметим терминологический вопрос.
Функция, имеющая в некоторой точке (или на некотором множестве) непрерывные частные производные, называется непрерывно дифференцируемой в этой точке (соответственно на множестве).
4.8. Касательная плоскость. Геометрический смысл дифференциала
1. Касательная плоскость и нормаль к поверхности. Геометрический смысл условия дифференцируемости.
В случае функции двух переменных z |
f (x, y) условию |
||
дифференцируемости |
можно |
дать |
геометрическую |
иллюстрацию. Введем |
понятие |
касательной плоскости к |
|
203

поверхности |
(т. |
е. |
графику функции f (x, y) ) |
в точке |
|||
P0 (x0 , y0 , z0 ) , z0 |
f (x0 , y0 ) . |
|
|
|
|
||
Определение 1. |
Плоскость |
, |
проходящая через точку |
||||
P0 поверхности, называется касательной плоскостью в этой |
|||||||
точке, если |
угол |
|
между |
этой |
плоскостью и |
секущей, |
|
проходящей через точку P0 |
и любую точку P поверхности, |
||||||
стремится к нулю, когда точка |
P |
стремится к точке P0 |
|||||
(рис. 59). |
|
|
|
|
|
|
|
касательная плоскость (
N
нормаль
Р
Р0
Рис. 59 |
|
Определение 2. Нормалью к поверхности |
P0 N в точке |
P0 называется прямая, проходящая через |
точку P0 |
перпендикулярно касательной плоскости к поверхности в этой точке.
Теорема. Пусть функция z  f (x, y) дифференцируема в точке M 0 (x0 , y0 ) . Тогда в точке P0 (x0 , y0 , z0 ) графика этой
f (x, y) дифференцируема в точке M 0 (x0 , y0 ) . Тогда в точке P0 (x0 , y0 , z0 ) графика этой
204

функции существует касательная плоскость, уравнение которой имеет вид
Z z0 f x (x0 , y0 )(x x0 ) |
f y (x0 , y0 )(y |
y0 ) . (4.37) |
|
Доказательство. |
Пусть |
функция |
z f (x, y) |
дифференцируема в точке M 0 (x0 , y0 ) . Тогда, в соответствии с
п.4.7. (формула (4.22)), |
можно записать |
при |
x x x0 , |
y y y0 |
|
|
|
Z z0 A(x |
x0 ) B( y y0 ) |
0( ) , |
(4.38) |
где А и В – постоянные, равные частным производным
функции |
f (x, y) |
в точке |
M 0 |
(см. п.4.7., формулы (4.27) и |
|||||
|
|
|
|
|
|
|
|
||
(4.28)), |
|
( |
x)2 |
( y)2 . |
Рассмотрим |
главную часть |
|||
приращения (1.38) функции z |
f (x, y) |
и введем функцию |
|||||||
(4.23) п.4.7. |
|
|
|
|
|
|
|
||
|
Z |
z0 |
A(x x0 ) |
B( y y0 ) , |
(4.39) |
||||
где A |
f x (x0 , y0 ) , |
B |
|
f y (x0 , y0 ) . |
Как |
известно из |
|||
аналитической геометрии, уравнение (4.39) в декартовой системе координат x, y, z определяет плоскость, проходящую через точку P0 (x0 , y0 , z0 ) , принадлежащую поверхности.
Нормальным вектором плоскости является вектор
N i f x (x0 , y0 ) 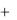 jf y (x0 , y0 ) k .
jf y (x0 , y0 ) k .
Докажем, что плоскость (4.39) является касательной плоскостью в точке P0 поверхности. Так как плоскость
проходит через точку P0 , то достаточно доказать, что угол  между нормалью N этой плоскости и любой секущей P0 P
между нормалью N этой плоскости и любой секущей P0 P
стремится к 2 , когда точка P поверхности стремится к точке
205

P0 |
. Поскольку |
|
|
|
|
|
|
|
|
(рис. 58), то это будет означать, что |
||
2 |
||||||||||||
|
|
|
|
|
|
|||||||
|
0 и по определению 1 плоскость будет являться |
|||||||||||
касательной плоскостью. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим cos |
|
N |
|
P0 P |
, где |
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
N |
|
|
P0 P |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
P0 P i (x x0 ) |
|
|
j( y y0 ) k (z z0 ) . |
|
|
|
|
|||||||||||||||||||||
Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
cos |
|
|
|
|
|
|
|
|
|
A(x x0 ) B( y y0 ) (z z0 ) |
|
|
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
A2 |
|
B 2 |
|
|
|
1 2 |
|
|
|
(x x0 )2 |
( y y0 )2 |
(z z0 )2 |
|||||||||||||||||
Из условия |
дифференцируемости |
функции |
z |
f (x, y) |
|||||||||||||||||||||||||||||
(4.38) следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
0( ) |
|
|
A(x x0 ) B( y y0 ) (z z0 ) . |
|
|
|
|
||||||||||||||||||||
Поэтому справедлива оценка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
cos |
|
|
|
|
|
|
|
|
0( |
) |
|
|
|
|
|
|
|
|
0( |
) |
|
0 при |
0 . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
(x x0 )2 |
( y y0 )2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Следовательно, lim |
|
|
|
|
|
|
и поэтому |
|
|
|
|
|
0 при |
||||||||||||||||||||
0 |
|
|
2 |
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 . Итак, плоскость (4.39) является касательной |
|||||||||||||||||||||||||||||||||
плоскостью в точке P0 |
к поверхности z |
|
|
|
f (x, y) . |
|
|
|
|
||||||||||||||||||||||||
Таким |
|
образом, |
|
|
|
дифференцируемость |
|
функции |
|||||||||||||||||||||||||
z f (x, y) в |
|
точке |
M 0 (x0 , y0 ) с |
геометрической точки |
|||||||||||||||||||||||||||||
зрения означает наличие касательной плоскости к графику функции z 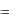 f (x, y) в точке P0 (x0 , y0 , z0 ) .
f (x, y) в точке P0 (x0 , y0 , z0 ) .
206

Учитывая, что коэффициенты А и В равны соответственно частным производным, вычисленным в точке M 0 (x0 , y0 ) , уравнение касательной плоскости может быть записано в виде
Z z0 |
z |
(M 0 )(x x0 ) |
|
z |
(M 0 )(y y0 ) . |
(4.40) |
|
x |
|
y |
|||||
|
|
|
|
|
|||
Нормальный |
вектор |
|
|
|
|
||
N |
f x (x0 , y0 ), f y (x0 , y0 ), 1 |
||||||
касательной плоскости называется вектором нормали к поверхности z  f (x, y) в точке P0 (x0 , y0 , z0 ) . Поскольку
f (x, y) в точке P0 (x0 , y0 , z0 ) . Поскольку
прямая P0 N перпендикулярна касательной плоскости в точке P0 , то ее направляющий вектор совпадает с нормалью N
касательной плоскости. Следовательно каноническое уравнение нормали имеет вид
x x0 |
|
y y0 |
|
z z0 |
. |
(4.41) |
f x (x0 , y0 ) |
|
f y (x0 , y0 ) |
1 |
|||
|
|
|
||||
2. Геометрический смысл полного дифференциала.
Вернемся к уравнению касательной плоскости (4.40).
Обозначив x |
x0 |
x , y |
y0 |
y , уравнение (4.40) запишем |
|
в виде |
|
|
|
|
|
Z |
z0 |
f x (x0 , y0 ) |
x f y (x0 , y0 ) y . |
(4.42) |
|
Правая часть уравнения (4.42) представляет собой полный |
|||||
дифференциал |
функции |
z |
f (x, y) в точке |
M 0 (x0 , y0 ) . |
|
Поэтому формулу (4.42) можно записать так: |
|
||||
|
|
Z |
z0 |
dz(M 0 ) , |
|
где левая часть равенства представляет собой приращение аппликаты касательной плоскости к поверхности (рис. 60).
207

поверхность z
P0
x |
M0(x0,y0) y |
x |
|
|
|
|
|
Рис. 60 |
P(x,y,z)
dz z
касательная
плоскость
y
M(x,y)
Таким образом, полный дифференциал функции двух
переменных |
в точке |
M 0 (x0 , y0 ) , |
соответствующий |
||
приращениям |
x и |
y |
независимых |
переменных, |
равен |
соответствующему |
приращению аппликаты касательной |
||||
плоскости к |
поверхности |
z f (x, y) , проведенной в |
точке |
||
P0 (x0 , y0 , z0 ) .
В этом заключается геометрический смысл полного дифференциала функции двух переменных.
4.9. Производные сложных функций. Производная по направлению и градиент. Экстремумы функции двух переменных
1. Производные сложных функций.
Пусть z  f (x, y) – функция двух переменных х и у, каждая из которых, в свою очередь, является функцией
f (x, y) – функция двух переменных х и у, каждая из которых, в свою очередь, является функцией
независимой переменной t: |
x x(t) , |
y y(t) . Тогда функция |
z f (x(t), y(t)) является |
сложной |
функцией независимой |
|
208 |
|

переменной |
t, а |
переменные |
х |
и |
у – промежуточные |
переменные. Имеет место следующая теорема. |
|||||
Теорема |
1. |
Если функции |
|
x x(t) и y y(t) |
|
дифференцируемы |
в точке |
t, |
а |
функция z f (x, y) |
|
дифференцируема в точке M (x(t), y(t)) , то сложная функция z  f (x(t), y(t)) также дифференцируема в точке t. При этом производная этой сложной функции вычисляется по формуле
f (x(t), y(t)) также дифференцируема в точке t. При этом производная этой сложной функции вычисляется по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
z dx |
|
|
z |
|
dy |
. |
|
|
|
|
|
|
|
|
|
|
(4.43) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
x dt |
|
|
y dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
З а м е ч а н и е. Обратите внимание на то, когда в |
||||||||||||||||||||||||||||||||||||||||||||||||
обозначениях производных пишется «д» и когда «d». |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1. |
|
Пусть z |
|
|
f (x, y) , |
|
x |
t3 2, y |
|
3t 4 |
1. |
|
По формуле |
|||||||||||||||||||||||||||||||||||||
(4.43) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
z |
3t 2 |
|
|
|
|
|
z |
12t3. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2. |
Пусть |
z |
|
xsin |
, |
x |
1 |
|
|
3t , |
|
y |
|
1 t 2 . |
По формуле |
|||||||||||||||||||||||||||||||||||
y |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(4.43) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
dz |
|
|
z dx |
|
|
z dy |
sin |
x x |
cos |
|
x |
3 |
|
|
x2 |
cos |
x |
|
|
t |
|
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
dt |
|
|
x dt |
|
|
y dt |
y y |
|
y |
|
|
y2 |
y |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t 2 |
||||||||||||||||||||||||||||||
3. |
|
Пусть |
|
|
z x2 y3, x |
|
|
t, |
y |
|
|
t 2. |
|
По |
формуле (4.43) |
|||||||||||||||||||||||||||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
2xy3 1 3x2 y2 2t. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Учитывая, что x |
t, |
|
y |
|
|
t 2 , находим |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
dz |
2t(t 2 )3 |
|
3t 2 (t 2 )2 2t |
|
|
8t7 . С другой стороны, можно |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
dt |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
209
