3530

знаем из п.4.2, графиком такой функции является некоторая поверхность в трехмерном пространстве. Фиксируя аргумент y y0 , мы получим плоскую кривую (lx ) , представляющую

собой сечение поверхности плоскостью, параллельной

направлением оси Ox .

Поскольку по определению частной производной (п.4.1)

то на основании геометрического смысла производной функции одной переменной, заключаем (рис. 57)

z

x (M 0 ) tg .

z

y

B

x

A

Рис. 57

190

Oy касательной P0 B к кривой (l y ) в точке P0 (x0 , y0 , z0 ) , то

существования частных производных в некоторой точке, вообще говоря, не вытекает непрерывность функции многих переменных в этой точке. Рассмотрим, например, функцию

В остальных точках (x, y) плоскости существование

производных очевидно.

Но если частные производные существуют и ограничены, то функция будет непрерывной. Это свойство выражается следующим утверждением.

Теорема. Если функция z 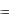имеет частные

производные по х и по у всюду в области D и эти производные всюду удовлетворяют неравенствам

191

производных - формулы (4.11) и (4.12), пригодно для внутренних точек области. Но для граничных точек этой области, вообще говоря, непригодно. Это связано с тем, что в граничных точках области задания функции (рис.58) не всегда можно вычислить частные приращения функции. В связи с этим принято определять частные производные функций в

x

Рис. 58

4.7. Дифференцируемость функций нескольких переменных. Полный дифференциал

Между локальными характеристиками функций одной и нескольких переменных имеются коренные различия. Если функция одной переменной имеет производную в точке x0 (

непрерывной в точке x x0 , а в окрестности этой точки она

192

может быть с высокой точностью приближена линейной функцией

В случае функции нескольких переменных уже нельзя рассчитывать на то, что из существования частных производных в точке будут вытекать такие же привлекательные следствия. В п.4.6 мы убедились на примере, что существование частных производных в точке О(0,0) (см. дополнительный материал п. 4.6) не обеспечило непрерывность функции в этой точке. Такое поведение функции нескольких переменных объяснимо из общих соображений. При вычислении частных производных функции двух или более переменных мы используем значения функции только на проходящих через данную точку отрезках прямых, параллельных координатным осям и не привлекаем в

193

рассмотрение все другие направления. Поэтому из существования частных производных не вытекает даже непрерывность функции.

1. Понятие дифференцируемости функции нескольких переменных и полного дифференциала.

Понятие дифференцируемой функции естественным путем распространяется на функции от двух или многих переменных. Окажется при этом, что все дифференцируемые функции обладают частными производными, а функции с

непрерывными частными производными будут дифференцируемы.

Определение 1. Функция u f (x, y) , определенная в точке M 0 (x0 ; y0 ) и в окрестности этой точки, называется дифференцируемой в точке M 0 , если ее полное приращение в этой точке может быть представлено в виде

Аналогичное определение дифференцируемости дается для функции большего числа переменных: u f (x1,..., xn )

называется дифференцируемой в точке M 0 (x10 ,..., xn0 ) , если ее

полное приращение имеет структуру

194

Чтобы пояснить смысл определения дифференцируемости функции u f (x, y) , заметим, что функция

собой погрешность, которую мы получим, заменяя данную

малой, значительно меньше этого расстояния.

В формулах для приращения дифференцируемой функции (4.18) – (4.20), (4.22), если хотя бы одно из чисел А, В (или одно

линейную относительно приращений аргументов часть приращения дифференцируемой функции. При определении понятия дифференцируемости функции не исключалась возможность обращения всех чисел А и В (или всех чисел Ak в

называется главная часть приращения функции в точке, линейная относительно приращений x и y переменных х и

196

выражения (4.24) или (4.25) для полного дифференциала не имеют законченной формы. В следующей части мы уточним эти формулы.

2. Следствия, вытекающие из дифференцируемости функции. Необходимые условия дифференцируемости. Законченный вид условия дифференцируемости и формулы для

В соответствии с определением непрерывности функции (см. п. 4.5) это и означает, что функция непрерывна в точке

M 0 .

Теорема 2. Если функция u f (x, y) дифференцируема в точке M 0 (x0 , y0 ) , то в этой точке существуют частные

197

производные по всем аргументам, причем A f x (x0 , y0 ) ,

B f y (x0 , y0 ) .

соответствии с условием дифференцируемости в формуле

Следствие. Условие дифференцируемости (4.22) в точке M 0 (x0 , y0 ) можно записать в следующей форме

198

(4.29)

Полный дифференциал функции u f (x, y) в точке M 0 (x0 , y0 ) записывается в окончательном виде

где дифференциалы независимых переменных равны их приращениям dx x , dy y .

З а м е ч а н и е 1 . Для функции n переменных условие (4.29) и формула (4.30) принимают вид

дифференциальное выражение

x1 ,..., xn ,

называемое оператором Гамильтона в n-мерном пространстве, то формулы (4.31) можно записать в виде скалярного произведения векторов u и dr :

u u(M 0 ) dr 0( ) , du(M 0 ) u(M 0 ) dr .

В трехмерном случае вектор dr и оператор Гамильтона имеют вид

199