
3530
.pdf
Решение. Используя известное из элементарной
математики |
неравенство |
x2 |
xy y2 |
|
xy |
получим, (при |
||||||||||||||||
x 0 и y |
0 ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
x |
y |
|
|
x y |
|
1 |
1 |
|
1 |
|
1 |
. |
||||||||
|
|
|
|
|
|
|||||||||||||||||
|
x2 |
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
xy |
|
xy |
|
y |
|
|
x |
|
|
|
|
y |
|
x |
|
|||||
Отсюда следует, что: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
lim |
|
x y |
|
|
lim |
1 |
|
1 |
|
0 . |
||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x2 |
|
|
y 2 |
|
|
y |
|
|
|
x |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
xy |
|
x |
|
|
|
|
|
|
|
|
|||||||||
|
|
y |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, предел данной функции равен нулю.
3. Бесконечно малые функции. |
|
||
Функция u f (M ) называется |
бесконечно |
малой при |
|
M M 0 |
(или в точке M 0 ), если |
lim f (M ) |
0 . |
|
M |
M 0 |
|
Используя определение предела функции в форме Коши (определение 2), можно придать определению бесконечно малой функции более содержательную форму.
Определение. (в форме Коши). Функция u  f (M )
f (M )
называется бесконечно малой, если, каково бы ни было малое положительное число , существует соответствующее ему
число |
такое, что |
для |
любой точки М из |
области |
||
определения |
функции, |
удовлетворяющей |
условию |
|||
(M , M 0 ) |
|
, абсолютная величина значений функции f (M ) |
||||
будет меньше |
: |
f (M ) |
. |
|
|
|
|
|
|
|
|
|
|
Следующая теорема устанавливает связь между предельным значением функции и бесконечно малой в окрестности предельной точки.
170

Теорема 3. Если функция u  f (M ) представляется в
f (M ) представляется в
виде f (M ) b |
|
|
(M ) , |
где b – постоянная, |
|
(M ) |
– |
|||||||||||||||||||
бесконечно малая функция при M |
|
M 0 , то |
lim |
f (M ) |
|
b . |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
M 0 |
|
|
|
|
|
|
Обратно, если |
lim |
f (M ) b , то f (M ) |
|
|
b |
(M ) , где |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
M |
M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(M ) – бесконечно малая функция при M |
M 0 . |
|
|
|
|
||||||||||||||||||||
|
|
Доказательство. Прямое утверждение. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Пусть |
|
функция u |
f (M ) может быть |
представлена |
в |
|||||||||||||||||||
виде f (M ) |
|
b |
|
(M ) , где b – постоянная, |
(M ) - бесконечно |
|||||||||||||||||||||
малая |
при |
|
M |
|
|
|
M 0 . Отсюда имеем: f (M ) |
|
b |
(M ) , т.е. |
||||||||||||||||
|
f (M ) b |
|
|
(M ) |
|
. При |
M |
M 0 |
|
|
(M ) |
|
, так |
как |
(M ) |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
– бесконечно малая функция, |
|
– любое сколь угодно малое |
||||||||||||||||||||||||
число. Поэтому существует такая |
|
– окрестность точки |
M 0 , |
|||||||||||||||||||||||
что для всех точек М из этой окрестности |
|
|
f (M ) |
b |
|
. |
||||||||||||||||||||
Поэтому |
lim |
f (M ) |
b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
M |
|
M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратное |
утверждение. |
Пусть |
lim |
f (M ) |
b . |
Это |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
M 0 |
|
|
|
|
|
|
|
|
значит, что при всяком |
|
0 |
существует |
|
– окрестность |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
точки |
M 0 , для |
|
|
всех |
точек |
М из |
которой |
|
|
f (M ) |
b |
|
. |
|||||||||||||
|
|
|
(M ) |
|
|
|
|
|||||||||||||||||||
Обозначим f (M ) |
b |
(M ) . Тогда |
|
|
. |
|
Но последнее |
|||||||||||||||||||
и |
означает, что |
|
|
|
(M ) |
– |
бесконечно малая |
|
функция |
при |
||||||||||||||||
|
M |
|
M 0 . Таким образом: |
f (M ) |
b |
(M ) . |
|
|
|
|
|
|
|
|||||||||||||
|
|
Бесконечно |
|
|
|
большая |
|
функция. |
Будем |
|
писать |
|||||||||||||||
|
|
lim |
f (M ) |
, |
если |
функция |
f (M ) |
|
определена |
в |
||||||||||||||||
|
M |
M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
некоторой |
окрестности |
точки |
|
M 0 , |
за исключением, быть |
|||||||||||||||||||||
может, самой точки M 0 , и для всякого N |
0 найдется |
|
|
0 |
||||||||||||||||||||||
171

такое, что |
f (M ) |
N , как только 0 (M , M 0 ) |
, для всех |
точек М, принадлежащих - окрестности точки M 0 . |
|||
4. Повторные пределы*. Для функции u |
f (x1,..., xn ) |
||
нескольких переменных можно определить понятие предела по одной из переменных xm при фиксированных значениях
остальных переменных. В связи с этим возникает понятие повторного предела.
Рассмотрим для простоты функцию двух переменных. |
|
||||||||||||||
|
|
Пусть |
функция |
z |
f (x, y) задана в |
|
|
некоторой |
|||||||
прямоугольной окрестности |
точки M 0 (x0 , y0 ) |
|
x |
x0 |
|
d1 , |
|||||||||
|
|
||||||||||||||
|
y |
y0 |
|
d2 , за исключением, быть может, |
самой точки |
M 0 . |
|||||||||
|
|
||||||||||||||
Пусть |
|
для |
каждого фиксированного |
y , |
удовлетворяющего |
||||||||||
|
|
|
|
|
|
||||||||||
условию |
0 |
y y0 |
d2 , |
существует |
предел |
функции |
|||||||||
|
z |
f (x, y) |
одной переменной x в точке x |
x0 : |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
lim |
f (x, y) |
( y) . |
|
|
|
|
|
|
|
|
|
|
|
|
x |
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
фикс. |
|
|
|
|
|
|
|
|
Пусть, кроме того, существует предел b функции |
|
( y) в точке |
|||||||||||||
|
y |
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
( y) b . |
|
|
|
|
|
|
|
yy0
Вэтом случае говорят, что существует повторный предел b для
функции z f (x, y) |
в |
точке |
M 0 , |
который обозначается |
следующим образом: |
|
|
|
|
lim |
lim |
f (x, y) |
b . |
|
y |
y0 |
x x0 |
|
|
______________________________________________________
*) Этот раздел предназначен для самостоятельного изучения.
172

Другой повторный предел получится, если вначале
устремить |
y |
y0 , |
т.е. |
при |
фиксированном |
x, |
удовлетворяющим условию 0 |
x x0 |
d1 , получить предел |
|
|||
|
|
lim |
f (x, y) |
(x) , |
|
|
yy0
x фикс.
азатем при x x0 получить повторный предел
lim |
lim f (x, y) B . |
x x0 |
y y0 |
З а м е ч а н и е . |
Не следует думать, что числа b и B |
обязательно совпадают, они могут и отличаться друг от друга.
|
Пример 6. Вычислить повторные пределы при |
x 0, |
||||||||||||||||
y |
0 |
от функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x, y) |
|
|
x2 |
y 2 |
x |
|
y |
. |
|
|
|
|||
|
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение. |
1) |
|
Вычислим |
|
повторный |
предел |
|||||||||||
lim |
lim f (x, y) |
. Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|||||
y 0 |
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
x2 |
y 2 |
|
x |
y |
y |
1 |
|
( y) ; |
|
|
|||||
|
|
|
|
x |
|
y |
|
|
|
|
|
|||||||
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
lim |
( y) |
|
|
lim ( y |
1) |
1 |
|
b . |
|
|
||||||
|
|
y |
|
0 |
|
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
|
2) Вычислим повторный предел lim |
lim |
f (x, y) . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
y |
0 |
|
|
|
|
|
lim f (x, y) |
|
lim |
x 2 |
y 2 |
x |
y |
1 |
x |
(x) ; |
|
||||||
|
|
|
|
|
|
x y |
|
|
|
|
||||||||
|
|
y 0 |
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
lim |
|
(x) |
|
|
lim (x |
1) |
1 |
B . |
|
|
||||||
|
|
x |
|
0 |
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
173

|
Таким образом, |
|
для данной функции повторные пределы |
||||||||||||||
не совпадают: b |
B . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример 7. |
Вычислить повторные пределы функции |
|||||||||||||||
|
|
|
|
|
|
|
|
f (x, y) |
|
2xy |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x2 |
y 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в точке O(0,0) (см. пример 1). |
|
|
|
|
|
|
|
|
|||||||||
|
Решение. |
|
|
|
1) |
|
|
Вычислим |
|
|
повторный |
предел |
|||||
lim |
lim f (x, y) |
. Имеем: |
|
|
|
|
|
|
|
|
|||||||
x 0 |
y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
2xy |
|
0 |
|
(x) ; |
lim |
(x) |
0 . |
|
|||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
y |
0 x2 |
y 2 |
|
|
|
x |
0 |
|
|
|
|||||
|
2) |
Вычислим повторный |
|
предел |
|
lim |
lim |
f (x, y) . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 0 |
x 0 |
|
Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
lim |
|
|
2xy |
|
0 |
( y) ; |
lim |
( y) |
0 . |
|
|||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
x |
0 x2 |
y 2 |
|
|
|
y |
0 |
|
|
|
|||||
Таким образом, для данной функции повторные пределы оказались равными. Однако, в примере 1 показано, что предел этой функции в точке O(0,0) не существует. На основании
этого результата можно сделать вывод: из существования и равенства повторных пределов функции в данной точке не следует существования предела функции в этой точке.
Из результата решения примера 6 следует, что, вообще говоря, нельзя допускать перестановку предельных переходов в повторных пределах.
Следующая теорема устанавливает достаточные условия
равенства двух |
введенных повторных пределов. |
|
|
|
|
|||||
|
Теорема |
4. Пусть функция z f (x, y) |
определена в |
|||||||
некоторой |
|
прямоугольной |
окрестности |
|
x x0 |
|
d1 , |
|||
|
|
|
||||||||
|
y y0 |
|
d2 |
точки M 0 (x0 , y0 ) |
и имеет в этой точке предел, |
|||||
|
|
|||||||||
174

равный b. Пусть, кроме того, для любого фиксированного х,
удовлетворяющего |
условию |
0 |
|
x |
x0 |
|
d1 , |
|
существует |
||||||||||||||||
предел |
(x) |
lim |
f (x, y) |
и |
для любого фиксированного |
y , |
|||||||||||||||||||
|
|
|
|
|
y y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
y |
y0 |
|
d2 , существует предел |
|
( y) |
lim |
f (x, y) . |
|
|||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Тогда |
повторные |
пределы |
|
|
|
|
|
|
x x0 |
|
|
|
|
и |
|||||||||
|
|
|
lim |
lim |
f (x, y) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x0 |
y |
y0 |
|
|
|
|
|
||
|
lim |
lim |
f (x, y) |
существуют и оба равны b . |
|
|
|
|
|
||||||||||||||||
y |
|
y0 |
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
Так как функция |
f (x, y) |
имеет в точке |
||||||||||||||||||||
M 0 (x0 , y0 ) |
предел, равный b, то для любого |
|
|
|
0 можно |
||||||||||||||||||||
|
|
0 , |
|
|
|
|
|
x |
x0 |
|
|
|
|
|
y |
y0 |
|
|
|||||||
указать |
такое |
что |
|
при |
|
|
|
и |
|
|
|
||||||||||||||
выполняется |
неравенство |
|
|
f (x, y) |
b |
|
|
|
. |
|
То |
есть |
в |
||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
прямоугольной окрестности |
|
x |
x0 |
|
|
, |
|
y |
y0 |
|
|
|
точки M 0 |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
значения функции f (x, y) отличаются от числа b не более чем на . Но тогда пределы функций (x) и ( y) , указанные в условии теоремы при х и у, удовлетворяющих неравенствам
|
x x0 |
и |
y y0 |
, так же отличаются от числа b не |
более чем на . |
|
|||
|
Следовательно, |
пределы этих функций в точках x0 и y0 |
||
соответственно существуют и равны этому числу b. Теорема доказана.
4.5. |
Непрерывность функции нескольких переменных |
||
1. |
Непрерывность функции в точке и на множестве. |
||
Интуитивно непрерывность функции z |
f (x, y) в точке |
||
M 0 (x0 , y0 ) можно представить себе так: |
во |
всех точках |
|
M (x, y) , близких к точке M 0 , значения функции |
f (x, y) мало |
||
175

отличаются от числа f (x0 , y0 ) , и даже сколь угодно мало, если только точки M достаточно близки к M 0 . Большей ясности
этого понятия можно добиться, уточнив термины – “близки”, “мало отличаются”, “сколь угодно близки”.
Определение 1. |
Функция |
z |
f (x, y) , определенная в |
||||||||||||
области |
D |
|
R 2 , |
называется |
непрерывной |
в |
точке |
||||||||
M 0 (x0 , y0 ) |
этой области, |
если для всякого |
|
0 возможно |
|||||||||||
найти такое |
|
( ) |
0 (вообще говоря зависящее от |
и |
|||||||||||
стремящееся к нулю вместе с |
), что для всех точек области |
||||||||||||||
D , расстояние которых от точки M 0 |
не превышает |
, т.е. |
|||||||||||||
для которых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(M , M |
0 |
) |
|
или |
(x |
x |
)2 |
( y y |
0 |
)2 |
2 , |
|
(4.3) |
||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
выполняется равенство |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
f (x, y) f (x0 , y0 ) |
|
|
. |
|
|
|
|
(4.4) |
|||
|
|
|
|
|
|
|
|
|
|
||||||
З а м е ч а н и е . Если |
точка |
M 0 (x0 , y0 ) - |
внутренняя |
||||||||||||
точка области |
D , то точки |
M (x, y) |
при достаточно малом |
||||||||||||
заполняют весь круг |
(M , M 0 ) |
|
|
(рис. 53а). Если же точка |
|||||||||||
M 0 - граничная (рис. |
53б), то точки M (x, y) |
заполняют лишь |
|||||||||||||
ту часть круга, которая принадлежит области D . |
|
|
|
||||||||||||
y |
|
|
а) |
|
|
б) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
M0 |
|
|
|
|
|
|
||
|
M0 |
|
|
D |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
 x
x
Рис. 53
176

Из определения 1 вытекает формальное определение непрерывности функции в точке.
Определение 2. Функция z  f (x, y) называется непрерывной в точке M 0 (x0 , y0 ) , если предел этой функции в
f (x, y) называется непрерывной в точке M 0 (x0 , y0 ) , если предел этой функции в
точке M 0 |
существует и равен значению функции f (x0 , y0 ) в |
|||||||
этой точке |
|
|
|
|
|
|
||
lim f (x, y) |
f (x0 , y0 ) |
или |
lim |
f (M ) f (M 0 ) . |
(4.5) |
|||
x |
x0 |
|
|
|
M |
M0 |
|
|
y |
y0 |
|
|
|
|
|
|
|
Поскольку |
M 0 |
lim M , |
то |
условие |
непрерывности |
(4.5) |
||
|
|
|
M M0 |
|
|
|
|
|
можно символически записать в виде |
|
|
||||||
|
|
lim f (M ) |
f ( |
lim |
M ) . |
|
(4.6) |
|
|
|
M |
M0 |
M |
M0 |
|
|
|
Формула (4.6) означает, что две операции – предельный переход и f , можно менять местами. То есть непрерывность функции означает возможность коммутации этих операций lim f () 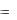 f (lim).
f (lim).
Точки пространства R 2 , в которых функция z  f (x, y)
f (x, y)
не обладает свойством непрерывности, называются точками разрыва этой функции.
Отметим, что на функции трех или большего числа переменных данные выше определения непрерывности переносятся без труда.
Можно сформулировать еще одно важное определение непрерывности функции U  f M
f M  в точке M 0 , если
в точке M 0 , если
использовать понятие открытого шара (смотри п. 4.1) и рассматривать функцию как отображение множеств (п. 4.3). Обозначим символом Ш (M0, r1, X ) - открытый шар радиуса r1
с центром в точке M 0 в пространстве X , символом
177

Ш ( f (M 0 ), r2 ,Y ) - открытый шар в пространстве Y с центром
в |
точке |
f (M 0 ) |
и радиусом r2 (оба пространства |
X |
и |
Y |
|||
предполагаются |
наделенными расстоянием между |
точками, |
|||||||
т. е. евклидовыми пространствами (п. 4.1)). |
|
|
|
|
|||||
|
Определение |
3. Функция |
f : X Y , |
где |
X |
R n , |
|||
Y |
R m , называется непрерывной в точке M 0 |
из X , если для |
|||||||
каждого шара |
Ш ( f (M 0 ), ,Y ) в Y существует такой шар |
||||||||
Ш (M 0 , |
, X ) в |
X , образ которого при отображении |
f |
||||||
содержится в указанном шаре в пространстве Y . То есть, |
|||||||||
если f (Ш (M 0 , |
)) |
Ш ( f (M 0 ), |
) . |
|
|
|
|
||
|
На рисунке 54, иллюстрирующем определение |
||||||||
непрерывности, |
множества X и Y изображены |
в |
виде |
||||||
плоскостей, т. е. оба они являются подмножествами |
R 2 . |
В |
|||||||
этом случае открытые шары являются открытыми кругами с
центрами в точках M 0 и f (M 0 ) |
соответственно. Стрелки |
|
показывают, что точки из |
Ш (M 0 , ) |
переводятся |
отображением f в точки Ш ( f (M 0 ), |
) . |
|
|
|
Y |
|
f(M0) |
|
M0 |
|
|
X |
|
|
Рис. 54 |
|
|
178

В математическом анализе ряд важных характеристик функций выражается через ее приращения. Иногда удобно использовать это понятие для определения непрерывности
функции. |
|
|
|
|
|
|
|
|
Назовем полным |
приращением |
функции |
u |
f (M ) в |
||||
точке M 0 , |
соответствующим приращению аргумента M 0M , |
|||||||
разность |
|
|
|
|
|
|
|
|
u |
f (M ) f (M |
0 |
) |
f (x ,..., x |
n |
) f (x0 ,..., x0 ) , |
(4.7) |
|
|
|
|
1 |
1 |
n |
|
||
где M 0 (x10 ,..., xn0 ) и M (x1,..., xn ) принадлежат области задания
функции. Если обозначить x1 x1 x10 ,..., xn xn xn0 , то
выражение для полного приращения функции можно записать в виде:
|
u f (x0 |
x ,..., x0 |
x |
n |
) |
f (x0 ,..., x |
0 ) . |
(4.8) |
||
|
1 |
|
1 |
n |
|
|
1 |
n |
|
|
|
Для функции двух переменных полное приращение |
|||||||||
функции в точке |
|
M 0 (x0 , y0 ) , соответствующее приращению |
||||||||
независимых переменных x, |
y , записывается в форме |
|
||||||||
|
z f (x0 |
x, y0 |
y) f (x0 , y0 ) . |
|
(4.9) |
|||||
|
Поэтому формулу (4.5) в определении 2 непрерывной |
|||||||||
функции |
|
можно |
|
|
|
записать |
|
так: |
||
lim lim f (x0 |
x, y0 |
y) |
f (x0 , y0 ) |
0 . |
|
|
||||
x |
x0 |
|
|
|
|
|
|
|
|
|
y |
y0 |
|
|
|
|
|
|
|
|
|
Отсюда следует: для непрерывности функции z  f (x, y) в точке M 0 (x0 , y0 ) необходимо и достаточно, чтобы ее полное приращение z представляло собой бесконечно малую в точке M 0 (x0 , y0 ) функцию, т. е. необходимо и достаточно, чтобы
f (x, y) в точке M 0 (x0 , y0 ) необходимо и достаточно, чтобы ее полное приращение z представляло собой бесконечно малую в точке M 0 (x0 , y0 ) функцию, т. е. необходимо и достаточно, чтобы
179
