3530

ных, ящик автоматически реагирует – изменяет длину стержня u – выходной (зависимой) переменной.

При желании операторный ящик можно воображать как радиотехнический прибор, преобразующий входные сигналы в выходные. Такая описательная модель допускает очевидное обобщение: если имеется несколько величин u1 , u2 ..., um ,

значение каждой из которых определяется значениями переменных x1 , x2 ..., xn , то имеем модель зависимости двух

векторных величин u (u1, u2 ,..., um ) и x (x1, x2 ,..., xn ) , принадлежащих пространствам разной размерности и возможно даже разной природы (рис. 43).

u2

Рис. 43 Функциональный ящик для зависимости векторных величин

2. Функция и область ее задания.

После этих замечаний, апеллирующих к наглядности, мы можем ввести фундаментальное математическое понятие функции n переменных.

Определение. Если каждой точке М из множества {М} точек n-мерного пространства E n ставится в соответствие

150

этом множество {М} называется областью задания функции u f (M ) .

Число u , соответствующее данной точке М из множества {М} называется частным значением функции в точке М. Совокупность {u} всех частных значений функции u f (M ) называется множеством значений этой функции.

Для функции u f (M ) используется также обозначение u f (x1,..., xn ) , где x1, x2 ..., xn – координаты точки М, или обозначение u

Таким образом, функция двух переменных ставит в соответствие каждой упорядоченной паре чисел (х,у), т. е. точке M (x, y) , принадлежащей некоторому подмножеству

точек плоскости, одно число (х,у) u ; функция трех переменных – упорядоченной тройке чисел (x, y, z) также сопоставляет вещественное число (х,у,z) u .

Как и прежде, для функции одной переменной, примем соглашение: в случае, когда функция определена некоторой формулой, и если только не оговорено противное, мы принимаем за область задания этой функции (область определения) наибольшее множество наборов чисел (x1,..., xn )

, на которых формула имеет смысл.

Рассмотрим примеры функций, заданных формулами.

Пример 1. u a2 x2 y2 , где а – действительное число. Областью определения этой функции является

x2 y2 a2 , т. е. замкнутый двумерный шар – круг радиуса а

151

с центром в начале координат. Множество значений функции – сегмент 0 u a .

Пример 2. u (x2 y 2 a2 ) 1 . Область задания этой функции является множество точек плоскости, лежащих вне круга радиуса а с центром в начале координат: x2 y2 a2 . Множество значений представляет собой открытую полупрямую u 0 (рис. 44).

y

Рис. 44. Область определения функции в примере 2 – внешность круга

Пример 3. u ln( y2 4x 8) . Область задания функции

–множество точек плоскости, координаты которых

удовлетворяют неравенству y2 4x 8 0 . Граница этой области (не входит в область определения!) – парабола, уравнение которой y2 4(x 2) .

Таким образом, границей области задания функции является парабола, ось которой совпадает с осью Ox , а

152

ординаты, чем точки, лежащие на границе области. Для точек M1 и M 2 ординаты удовлетворяют неравенству y2 4(x 2) ,

а для точек параболы - y 2 4(x 2) .

Следовательно, в область определения войдут те, и только те точки, которые лежат левее параболы. Это пример незамкнутой односвязной неограниченной области.

y

Рис. 45 Область определения функции в примере 3

Пример 4. u arcsin(x2 y2 3) . Область задания

Граничными линиями области определения являются

ограниченной неодносвязной области. Область 2 x2 y2 4

153

является двухсвязной, так как степень связности равна числу замкнутых кривых, ограничивающих область.

y

Рис. 46 Область определения функции в примере 4

3. Геометрическое изображение функций.

154

Подобно тому, как функцию одной переменной изображают в виде линии на плоскости – ее графика, можно геометрически истолковать и функции многих переменных. Однако график сохраняет наглядность только для функций двух переменных – в этом случае график представляется поверхностью в трехмерном пространстве.

y

Рис. 47 Область определения функции в примере 5

Определение. Графиком функции двух переменных u f (x, y) называется множество точек трехмерного пространства (x, y, f (x, y)) , если точка плоскости (x, y) принадлежит области задания функции, а значение функции – области значений.

Изображение функции двух переменных осуществляется так: строим прямоугольную систему координат х, у, z и относим каждой точке (x, y) области определения функции

точку P(x, y, z) с третьей координатой, равной f (x, y) . Когда точка (x,y) пробегает область определения функции, соответствующая точка P(x, y, f (x, y)) описывает в пространстве некоторую поверхность. Эту поверхность и

155

принимают за геометрическое изображение функции, то есть – график функции.

Пример 6. Изобразить график функции

z a2 x2 y2 . Областью задания этой функции, как мы

знаем, является круг с центром в начале координат и радиусом a. Графиком этой функции является верхняя половина сферы x2 y2 z 2 a2 (рис. 48).

z

a

a

x

y

Рис. 48 График функции в примере 6.

Если разрешить это уравнение относительно z, получим

полусфера, графиком другой – нижняя полусфера.

156

Пример 7. Изобразить график функции z x2 y2 . Областью определения этой функции является множество всех точек плоскости xOy , областью значений – полупрямая z 0 .

Функции z x2 y2 соответствует график – параболоид вращения (рис. 49). Это поверхность, описываемая параболой z x2 при ее вращении вокруг оси Oz .

z

0

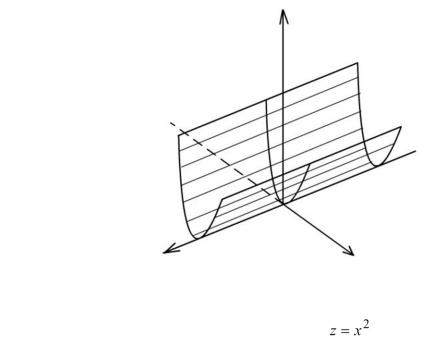
Пример 8. Изобразить график функции z x2

графиком является параболический цилиндр (рис. 50).

157

разработаны математические модели процессов управления и контроля, теоретической физики и экономики.

Определение. Если даны два множества X и Υ, то соответствие f , которое каждому элементу x из X относит некоторый элемент y, обозначаемый f (x) из Υ, называется функцией, определенной на множестве X со значениями в множестве Υ, или отображением ƒ множества X в множество Υ (рис. 51).

f

Y

X

f

Рис. 51 Функция, “склеивающая” образы двух точек.

областью определения (или областью задания), множества Υ,

f 1(B) .

159