
3530
.pdf
асимптотами. Существуют три вида асимптот: вертикальные,
горизонтальные и наклонные.
Определение 1. Прямая x x0 называется вертикальной асимптотой графика функции y  f (x) , если хотя бы одно из
f (x) , если хотя бы одно из
предельных значений |
lim f (x) или |
lim f (x) равно |
x |
x0 |
x x0 |
или  .
.
Вэтом случае расстояние от точки M (x; f (x)) до прямой
xx0 равно
d |
x x0 |
2 |
f (x) f (x) 2 |
|
x x0 |
|
и, следовательно, d 0 при х x0 .
Например, график функции y  f (x) 1 x (рис. 19) имеет вертикальную асимптоту x 0 , так как f (x)
f (x) 1 x (рис. 19) имеет вертикальную асимптоту x 0 , так как f (x) 
при |
х 0 и f (x) |
при х |
0 . |
|
||
|
Определение 2. |
|
Прямая |
y A |
называется |
|
горизонтальной асимптотой графика функции y |
f (x) при |
|||||
x |
( x |
), если lim |
f (x) |
A . |
|
|
|
|
|
x |
|
|
|
|
|
|
( x |
) |
|
|
Рис. 18 |
Рис. 19 |
30

В этом случае расстояние от точки M (x; f (x)) до прямой y A равно
d 
 (x x)2 ( f (x) A)2
(x x)2 ( f (x) A)2  f (x) A
f (x) A
и, |
следовательно, |
|
d |
0 |
|
при |
x |
, |
так |
|
|
|
как, |
|||||||||||||||
lim |
|
f (x) |
A |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
Например, график рассмотренной выше функции |
y |
1 |
|
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
имеет горизонтальную асимптоту |
y |
0 при |
x |
|
|
|
и при |
|||||||||||||||||||||
x |
|
, так как |
|
1 |
|
0 |
при |
x |
|
|
|
|
и при x |
|
. |
|
|
|
|
|
|
|||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Определение 3. |
Прямая |
y |
kx |
b ( k |
0 ) |
называется |
|||||||||||||||||||||
наклонной |
асимптотой |
графика |
|
функции |
y |
f (x) |
|
|
|
при |
||||||||||||||||||
x |
|
( x |
|
|
|
), если функцию f (x) |
можно представить в |
|||||||||||||||||||||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) kx b |
|
|
|
(x), |
|
|
|
|
|
|
(1.8) |
|||||||||
где |
|
(x) |
0 при x |
|
|
( x |
|
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Рассмотрим геометрический смысл наклонной асимптоты. |
|||||||||||||||||||||||||||
Для |
определенности |
разберем |
случай, |
когда |
x |
|
|
|
. |
|||||||||||||||||||
(Случай x |
|
|
|
рассматривается аналогично). |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Пусть M (x; y) |
– точка графика функции |
y |
f (x) |
|
и |
||||||||||||||||||||||
пусть прямая |
~ |
|
kx |
b |
является наклонной |
асимптотой |
||||||||||||||||||||||
y |
||||||||||||||||||||||||||||
графика функции при |
x |
|
. Текущую ординату точки на |
|||||||||||||||||||||||||
асимптоте |
обозначим |
|
|
~ |
точку на |
асимптоте |
– через |
|||||||||||||||||||||
через y , |
||||||||||||||||||||||||||||
|
~ |
|
|
|
|
|
|
MN |
|
|
y |
~ |
|
|
|
f (x) |
(kx |
b) |
|
|
(x) |
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
N(x; y) (рис.20).Тогда |
|
|
y |
|
|
|
|
|
|
|||||||||||||||||||
при x  . Опустим из точки М перпендикуляр МР на асимптоту. Расстояние d от точки М до асимптоты равно
. Опустим из точки М перпендикуляр МР на асимптоту. Расстояние d от точки М до асимптоты равно
MP
 MN cos , где
MN cos , где  угол между асимптотой и осью Ох, и,
угол между асимптотой и осью Ох, и,
следовательно, lim d 0 .
x
31

Таким образом, расстояние от точки M (x; y) |
графика |
функции до асимптоты стремится к нулю при х |
+ , т.е. |
график функции неограниченно приближается к асимптоте при
х + .
Рассмотрим способ отыскания наклонной асимптоты, т.е. способ определения чисел k и b в уравнении асимптоты. Разделив равенство (1.8) на х и перейдя к пределу при х + ,
получим lim |
f (x) |
|
|
lim |
k |
b |
|
|
(x) |
|
k. |
|
||
|
|
x |
x |
|
||||||||||
x |
x |
x |
|
|
|
|
||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
lim |
|
f (x) |
. |
|
(1.9) |
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
Далее, |
из |
|
соотношения |
(1.8) |
получаем: |
|||||||||
lim f (x) kx |
lim |
b |
(x) |
|
|
b. |
|
|
|
|
||||
x |
x |
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
b |
lim f (x) |
kx . |
|
(1.10) |
||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
Доказано, |
что |
|
если |
прямая |
~ |
kx b |
наклонная |
|||||||
|
y |
|||||||||||||
асимптота, то числа k и b находятся по формулам (1.9) и (1.10).
Обратно, если оба предела (1.9) и (1.10) существуют, причём |
|||||||||||
k 0 , |
то прямая |
~ |
kx |
b |
является наклонной |
асимптотой |
|||||
y |
|||||||||||
графика функции |
y |
f (x) |
при х + . |
|
|
|
|||||
В самом |
деле, |
полагая |
(x) |
f (x) |
kx |
b |
и используя |
||||
равенство (1.10), получаем, что |
lim |
(x) |
0 . Следовательно, |
||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
справедливо |
равенство |
|
(1.8): |
f (x) |
kx |
b |
(x) , где |
||||
lim |
(x) 0 , |
т.е. |
прямая |
~ |
kx |
b является |
наклонной |
||||
y |
|||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
асимптотой графика функции при x |
. |
|
|
|
|||||||
Практически целесообразно искать асимптоты в следующем порядке: 1) вертикальные асимптоты; 2) горизонтальные асимптоты; 3) наклонные асимптоты.
32

|
Пример |
|
6. |
Найти |
|
асимптоты |
|
|
графика |
функции |
||||||||||||||||||||||||||
y |
x2 |
2x |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. 1) Находим вертикальные асимптоты. Точка |
|||||||||||||||||||||||||||||||||||
x 0 - |
точка |
|
разрыва |
2-го |
рода данной функции, причем |
|||||||||||||||||||||||||||||||
y |
|
при x |
|
0 |
, y |
|
|
|
|
|
|
|
|
при x |
0 |
|
|
. Следовательно, |
||||||||||||||||||
ось ординат ( x |
|
0 ) |
вертикальная асимптота. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
2) Находим горизонтальные асимптоты |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
lim |
|
x 2 |
2x |
3 |
|
|
|
|
lim |
x |
2 |
3 |
|
|
|
|
|
( |
|
) , |
|||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
( x |
|
) |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
следовательно, горизонтальных асимптот нет. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
3) Находим наклонные асимптоты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
k |
|
lim |
f (x) |
|
|
|
lim |
1 |
|
2 |
|
|
3 |
|
1 |
, |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
x2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
( x |
) |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
lim |
f (x) |
kx |
|
|
|
|
lim |
|
x2 |
|
2x |
3 |
|
x |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
( x |
) |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
lim |
|
2x |
3 |
|
|
lim |
2 |
|
|
3 |
|
|
2 . |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
( x |
) |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
прямая |
|
|
y x 2 является наклонной |
|||||||||||||||||||||||||||||||
асимптотой графика данной функции как при |
x |
|
, так и |
|||||||||||||||||||||||||||||||||
при x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
График функции схематически изображен на рис. 21. |
|||||||||||||||||||||||||||||||||||
|
Пример 7. Доказать, |
что гипербола |
|
|
x2 |
|
|
|
y2 |
|
1 |
имеет |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
b2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
своими наклонными асимптотами прямые |
|
y |
|
|
|
|
|
b |
x . |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Так как |
|
y |
|
|
|
|
x |
2 |
a2 |
|
, то |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
33

|
|
|
b |
|
|
|
|
b |
x |
|
lim |
f (x) kx |
lim |
|
x2 |
a2 |
|||||
|
|
|||||||||
x |
|
x |
a |
|
|
|
|
a |
||
(x |
) |
x |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
a 2 |
|
|
|
lim |
|
|
x2 |
a2 x |
|
|
|
lim |
|
|
|
|
|
0. |
||||||
|
a |
|
|
a x |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2 |
|
2 |
||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
x |
a |
x |
|||||||
(x |
) |
|
|
|
|
|
|
|
(x |
|
|
) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, |
прямые |
|
|
b |
|
являются наклонными |
||||||||||||||
|
|
|
|
|
||||||||||||||||
y |
|
a x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
асимптотами данной гиперболы как при |
x |
|
|
, |
так и при |
|||||||||||||||
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 20 |
Рис. 21 |
8. Схема исследования графика функции. Рассмотрим примерную схему, по которой целесообразно исследовать поведение функции и строить ее график.
1. Найти область определения функции.
34

2.Найти точки пересечения графика функции с осями координат.
3.Найти асимптоты.
4.Найти точки возможного экстремума.
5.Найти критические точки.
6.С помощью вспомогательного чертежа исследовать знак первой и второй производных. Определить участки возрастания и убывания функции. Найти направление выпуклости графика, точки экстремума и точки перегиба.
7.Построить график, учитывая исследование, проведенное
вп. 1 6.
При этом в начале исследования полезно проверить, является данная функция четной или нечетной, чтобы при построении использовать симметрию графика относительно оси ординат или начала координат.
В качестве примера построим по изложенной выше схеме
график функции y |
x2 |
1 |
. |
|
x |
1 |
|
||
|
|
|
||
1. Областью определения функции является множество |
||||
всех действительных |
чисел, |
кроме x 1, при котором |
||
обращается в нуль знаменатель. |
|
|||
2. Так как уравнение x 2 |
1 0 не имеет действительных |
|||
корней, то график функции не имеет точек пересечения с осью
Ox, но пересекает ось Oy в точке (0; |
1) . |
|
|
|
||||
3. Выясним вопрос о существовании асимптот. Исследуем |
||||||||
поведение функции |
вблизи точки |
разрыва |
x 1. Так как |
|||||
y |
при x |
1 |
, y |
при |
x |
1 , |
то прямая |
x 1 |
является |
вертикальной |
асимптотой |
графика |
функции. |
Если |
|||
x |
( x |
), |
то |
y |
( y |
), |
следовательно, |
|
горизонтальной асимптоты у графика нет. Далее, из существования пределов
|
|
f (x) |
|
x 2 |
1 |
|
1 1/ x 2 |
||
k |
lim |
|
lim |
|
|
lim |
|
|
1, |
|
x 2 |
|
|
||||||
x |
|
x |
x |
x |
x |
|
1 1/ x |
||
( x |
) |
|
x |
|
|
( x |
) |
|
|
35

b |
lim f (x) kx |
|
lim |
x2 |
1 |
x |
|
|
x |
1 |
|
||||
x |
|
x |
|
|
|
||
(x |
) |
x |
|
|
|
|
|
|
|
|
|
|
lim |
1 |
x |
|
lim |
1 |
1/ x |
1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
x |
1 |
1 |
1/ x |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x |
|
|
|
|
|
( x |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
вытекает, что |
при |
x |
|
|
|
|
и при x |
|
|
график функции |
|||||||||||||||||||
имеет наклонную асимптоту |
y |
x |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
4. Для нахождения точек экстремума вычислим первую |
|||||||||||||||||||||||||||||
производную: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f |
(x) |
2x(x 1) (x2 |
1) |
|
2x2 |
|
2x x2 |
1 x2 |
2x 1 |
. |
|||||||||||||||||||
|
|
|
(x 1) |
2 |
|
|
|
|
|
|
|
(x 1)2 |
|
|
|
|
|
(x 1)2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решая |
уравнение |
x 2 |
2x |
1 |
0 , |
|
|
получаем |
|
|
две точки |
||||||||||||||||||
возможного экстремума: |
x1 |
1 |
|
2 |
|
|
и x2 1 |
2 . |
|
|
|
|
|||||||||||||||||
5. |
|
|
Для |
нахождения критических |
точек |
вычислим |
|||||||||||||||||||||||
вторую производную: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f (x) |
|
(2x |
2)(x |
1)2 |
|
2(x |
1)(x2 |
2x |
1) |
|
|
|
|
4 |
. |
|
|||||||||||||
|
|
|
|
|
|
|
(x 1)4 |
|
|
|
|
|
|
|
|
|
(x 1)3 |
|
|||||||||||
Так как |
f |
(x) |
в |
|
нуль |
не |
обращается, |
то |
|
критических |
|||||||||||||||||||
точек нет.
Нарисуем вспомогательный чертеж и исследуем знак первой и второй производных (рис.22). Получаем, что функция
на (  , 1
, 1
 2 ) возрастает, на (1
2 ) возрастает, на (1
 2, 1
2, 1
 2 ) убывает, а на ( 1
2 ) убывает, а на ( 1 
 2, ) снова возрастает.
2, ) снова возрастает.
Точки экстремума:
|
|
|
|
|
|
|
1) максимум при x 1 2 , причём |
f (1 2) 2 2 2 |
|||||
; 2) минимум при x 1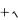
 2 , причём f (1
2 , причём f (1
 2) 2 2
2) 2 2
 2 . На (
2 . На (
 , 1) направление выпуклости графика вверх, а на (1,
, 1) направление выпуклости графика вверх, а на (1,  ) - вниз.
) - вниз.
36

Рис. 22
6. Используя полученные данные, строим эскиз графика
(рис. 23)
Рис. 23
37

|
|
|
Задачи |
к п. 1 |
||
1. |
Определить промежутки |
возрастания и убывания |
||||
функции: |
|
|
|
|
|
|
1) f (x) |
x3 |
5x 6; |
2) |
f (x) |
x 2 ; |
|
3) |
f (x) |
2x2 |
ln x |
(x |
0); |
|
4) |
f (x) 3x 2 |
3; |
5) |
f (x) x3 3x 2. |
||
2. Доказать, что функция f (x) 1 x3 убывает на всей
числовой прямой.
3. Найти максимумы и минимумы функций:
1) |
f (x) |
x2 |
x |
; |
2) f (x) xln x; |
|
x2 |
x 3 |
|||||
|
|
|
|
3) |
f (x) |
|
1 x4 |
2 |
x3 |
3 |
x2 |
2; |
||
|
|
|||||||||
|
|
4 |
|
3 |
2 |
|
|
|||
4) |
f (x) |
|
|
x |
; |
|
|
|
5) f (x) x 2e x . |
|
|
|
|
|
|
|
|||||
1 |
x2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
4. Решеткой длиной 120 метров нужно огородить прилегающую к дому прямоугольную площадку наибольшей площади. Определить размеры прямоугольной площадки.
5. Разложить число 10 на два слагаемых так, чтобы произведение их было наибольшим.
6. Определить наибольшую площадь прямоугольника, у которого одна сторона лежит на основании а данного треугольника, а две вершины – на боковых сторонах треугольника, если треугольник имеет высоту h.
7. Из квадратного листа картона со стороной а вырезают по углам одинаковые квадраты и из оставшейся крестообразной фигуры склеивается прямоугольная коробка. Какова должна быть сторона вырезаемого квадрата, чтобы объем коробки был наибольшим?
8. Определить размеры открытого бассейна с квадратным дном объемом V так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
38

9.Сечение тоннеля имеет форму прямоугольника, завершенного полукругом. Периметр сечения р. При каком радиусе полукруга площадь сечения будет наибольшей?
10.В прямой круговой конус радиуса R и высоты h вписан цилиндр наибольшего объема. Найти этот объем.
11.В шар радиуса R вписан цилиндр наибольшего объема. Найти этот объем.
12.Из сектора круга радиуса R свертывается коническая воронка. При каком центральном угле она имеет наибольший объем?
13.Даны точки А(0, 3) и В(4, 5). На оси Оx найти точку, сумма расстояний которой до точек А и В наименьшая.
14.Найти интервалы выпуклости и точки перегиба
графика функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
f (x) x3 |
|
6x2 x; |
2) f (x) x4 |
2x3 |
12x2 |
5x 2; |
|
|||||||||||
3) |
f (x) |
(x 1)4 ; |
|
4) f (x) |
|
2x2 |
|
|
; |
|
|
|
|
|
|||||
|
3 |
x |
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5) f (x) |
2x2 |
|
ln x; |
6) f (x) |
xarctgx. |
|
|
|
|
|
|||||||||
15. |
При каком значении а кривая y |
x3 |
ax2 |
1 имеет |
|||||||||||||||
точку перегиба при х = 1? |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
16. |
При каком значении а кривая |
y |
|
|
x4 |
ax3 |
|
3 |
x2 |
1 |
|||||||||
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
будет иметь выпуклость вниз на всей числовой прямой? |
|
||||||||||||||||||
17. Найти асимптоты графиков функций: |
|
|
|
|
|
||||||||||||||
1) |
f (x) |
|
5x |
; |
|
|
2) f (x) |
|
|
x |
|
|
x; |
|
|
|
|
||
|
x |
1 |
|
|
2x |
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3) |
f (x) |
|
x2 |
|
5 |
|
2x; |
4) f (x) |
|
xe1 x ; |
|
|
|
|
|
|
|||
|
x2 |
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5) |
f (x) |
x |
2arctgx. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Построить графики функций:
39
