
3530
.pdf
|
|
|
|
|
|
|
|
|
|
Рис. 10 |
|
|
|
|
|
|
|
|||
|
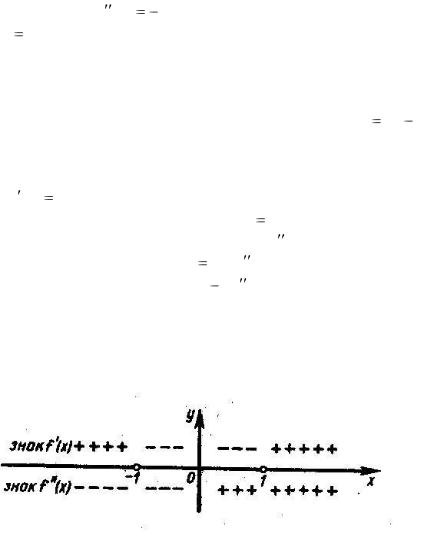
На |
рис.10 |
|
видны |
и интервалы |
монотонности |
f (x) : |
|||||||||||||
( |
, 1), ( 1, 1) |
и |
(1, |
|
), причем в первом и третьем |
из них |
||||||||||||||
функция возрастает, а во втором – убывает. |
|
|
|
|
|
|
||||||||||||||
|
3. Исследование функции на максимум и минимум с |
|||||||||||||||||||
помощью |
второй |
производной. |
|
Пусть |
|
при |
x |
x1 |
||||||||||||
производная |
|
функции |
y |
f (x) обращается |
в |
нуль, |
т.е. |
|||||||||||||
f |
(x1) |
0 . |
Пусть, |
кроме того, |
вторая производная |
f |
(x) |
|||||||||||||
существует и непрерывна в некоторой окрестности точки |
x1 . |
|||||||||||||||||||
Тогда справедлива следующая теорема. |
|
|
|
|
|
|
|
|||||||||||||
|
Теорема 10. |
Пусть |
f (x1) |
0 ; |
тогда при x |
|
x1 функция |
|||||||||||||
имеет максимум, если |
f (x1) |
|
0 , и минимум, если |
f (x1) |
0 . |
|||||||||||||||
|
Доказательство. |
|
Докажем |
сначала |
первую |
часть |
||||||||||||||
теоремы. Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
f (x1) 0 и f (x1) 0 . |
|
|
|
|
|
||||||||
|
Так как, по условию, |
f |
(x) |
непрерывна |
в некоторой |
|||||||||||||||
окрестности точки |
x |
x1 , то, очевидно, найдется некоторый |
||||||||||||||||||
малый отрезок, |
окружающий |
точку x |
x1 , |
во |
|
всех |
точках |
|||||||||||||
которого вторая производная |
f |
(x) будет отрицательной. |
|
|||||||||||||||||
|
Так |
как |
|
f |
(x) |
есть |
первая |
производная |
от |
первой |
||||||||||
производной, |
|
f |
(x) |
f (x) |
, |
|
то |
из |
условия |
|
f (x) |
0 |
||||||||
следует, |
что |
f |
(x) |
убывает |
на |
отрезке, |
содержащем |
точку |
||||||||||||
x |
x1 . Но, |
f |
(x1) |
0 , |
следовательно, |
на |
этом |
|
отрезке |
при |
||||||||||
x |
x1 имеем |
f |
(x) |
0, |
а при |
x |
x1 |
имеем |
f |
(x) |
0 , |
т.е. |
||||||||
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|

производная |
f |
(x) при переходе через точку x |
x1 меняет |
||||
знак с плюса на минус, а это значит, что в точке |
x1 функция |
||||||
f (x) имеет максимум. Первая часть теоремы доказана. |
|||||||
Аналогичным образом доказывается вторая часть |
|||||||
теоремы, а именно: если |
f (x1) |
0 , то f |
(x) |
0 во все точках |
|||
некоторого отрезка, окружающего точку |
x1 , |
но тогда на этом |
|||||
отрезке f (x) |
f (x) |
0 и, следовательно, |
f (x) возрастает. |
||||
Так как f (x1) |
0 , то, значит, |
при переходе через точку x1 |
|||||
производная |
f |
(x) меняет знак с минуса на плюс, т.е. функция |
|||||
f (x) имеет минимум при x x1 . |
|
|
|
|
|||
Если в |
критической точке |
f (x1) |
0 , |
то в |
этой точке |
||
может быть или максимум, или минимум или не не быть ни максимума, ни минимума. В этом случае исследование нужно вести с помощью первой производной.
Пример |
1. |
Исследовать на |
максимум |
и минимум |
|||||
функцию y x |
2sin x на отрезке [0, 2 |
]. |
|
|
|
||||
Решение. |
1) Находим критические точки: |
|
|
|
|||||
y |
1 2cos x, |
1 2cos x |
0, |
x1 |
3 , |
x2 |
5 |
3 . |
|
2) |
Находим |
вторую |
производную |
y |
2sin x и |
||||
определяем ее знак в точках |
x1 |
3 , |
x2 |
5 |
3. |
В точке |
|||
x1 |
3 имеем: |
y ( |
3) |
|
2sin |
|
3 |
|
3 |
|
0. В точке x2 5 3 |
|||||||
имеем: |
y (5 |
3) |
2sin5 |
|
3 |
|
3 |
|
0 . |
|
|
|
|
|
|
|
||
Следовательно, в точке x1 |
3 |
|
функция имеет минимум: |
|||||||||||||||
|
ymin |
|
3 |
2sin 3 |
|
|
|
3 |
|
|
3 |
|
|
|
0.68 , |
|||
а в точке x2 |
5 |
3 |
функция имеет максимум: |
|
||||||||||||||
|
ymax |
|
5 3 |
2sin 5 |
3 |
|
5 3 |
|
3 |
|
6.96 . |
|||||||
Пример |
|
2. |
|
Исследовать на максимум и минимум |
||||||||||||||
функцию y |
1 |
x4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. |
1) Находим критические точки: |
|
||||||||||||||||
21

y |
4x3 , |
4x3 0, x 0 . |
2) Определяем знак второй производной при x 0 : y
 12x2 , ( y
12x2 , ( y ) x 0 0.
) x 0 0.
Следовательно, выяснить характер критической точки с помощью второй производной в данном случае нельзя.
3) Исследуем характер критической точки с помощью первой производной
( y ) x 0 |
0 , |
( y ) x 0 |
0 . |
|
|
Следовательно, при |
x 0 |
функция |
имеет максимум, |
а |
|
именно: |
|
|
|
|
|
( ymax ) x |
0 |
1. |
|
|
|
4. Отыскание наибольшего и наименьшего значений |
|||||
функции. Рассмотрим функцию y |
f (x) , непрерывную |
на |
|||
отрезке [a,b] . Как известно, такая функция достигает своего
наибольшего и наименьшего значений либо на границе отрезка, либо внутри него. Если наибольшее (или наименьшее) значение функции достигается во внутренней точке x0 отрезка,
то это значение является максимумом (или минимумом)
функции, |
так как |
неравенство |
M f (x0 ) |
f (x) (или |
m f (x0 ) |
f (x) ), имеющее место для всех точек |
x отрезка |
||
[a,b], выполняется и для любой окрестности |
точки x0 , |
|||
лежащей внутри отрезка [a,b] (см. рис. 7). |
|
|||
Таким |
образом, |
получаем |
следующее |
правило |
нахождения наибольшего и наименьшего значений функции на отрезке [a,b] .
1.Находим все критические точки функции в интервале (a,b) и вычисляем в них значения функции.
2.Вычисляем значения функции на концах отрезка – в
точках x a и x b .
3. Из всех этих значений выбираем наибольшее и наименьшее.
22

З а м е ч а н и е. Очевидно, если непрерывная на отрезке функция имеет во внутренней точке этого отрезка только один экстремум, то в этой точке она имеет наибольшее значение в случае максимума и наименьшее – в случае минимума.
Пример 3. Найти наибольшее и наименьшее значения
функции f (x) x3 |
3x на отрезке [ |
1.5;2.5] |
|
|
|
Решение. 1) Находим критические точки функции в |
|||||
интервале ( 1.5;2.5) : |
|
|
|
|
|
f (x) 3x2 |
3 , 3x2 3 0 , |
x |
1, x |
2 |
1. |
|
|
1 |
|
|
|
Вычисляем значения функции в этих точках:
|
f ( |
1) ( 1)3 |
3( |
1) |
2 , f (1) |
|
1 3 2 . |
|
|
2) |
Вычисляем значения функции на концах отрезка: |
||||||||
|
|
f ( 1.5) |
( |
1.5)3 |
|
3( 1.5) |
1.125 , |
|
|
|
|
f (2.5) |
(2.5)3 |
3 |
2.5 |
8.125. |
|
||
Таким |
образом, |
наибольшее |
|
значение |
функции |
||||
yнаиб |
8.125 |
достигается |
на |
правом |
конце |
отрезка. |
|||
Наименьшее значение функции yнаим  2 достигается в точке
2 достигается в точке
x1.
5.Применение теории максимума и минимума к решению задач. Изложенную теорию максимума и минимума функции можно применить к решению практических задач.
Пример 4. Из квадратного листа жести со стороной a требуется сделать открытый сверху ящик, возможно большего объема, вырезая равные квадратные уголки и загибая жесть (рис. 11). Какова должна быть сторона вырезаемых квадратных уголков?
Решение. Пусть сторона вырезаемого квадрата равна x ,
тогда сторона квадрата, |
образующего дно ящика, равна a 2x . |
|
Объем ящика |
|
|
V (a 2x)2 x a2 x 4ax2 |
4x3. |
|
Для решения задачи нужно определить наибольшее |
||
значение функции V |
в интервале |
(0, a 2) . Находим |
23

производную |
V |
a2 |
8ax |
12x2 . |
|
|
Решая |
|
уравнение |
||||||||
a2 8ax 12x2 |
0 , |
получаем |
критическую |
точку |
x |
a 6 , |
|||||||||||
принадлежащую указанному интервалу. Так как при x |
a 6 |
||||||||||||||||
вторая |
производная |
|
V |
|
8a |
|
24x |
|
отрицательна |
||||||||
[V (a 6) |
8a |
24 a 6 |
4a 0], |
|
то |
в точке |
x |
a 6 |
объем |
||||||||
достигает максимума: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
V |
|
a |
|
2a |
2 a |
|
2 |
a3 . |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
max |
|
6 |
|
6 |
|
27 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Согласно, |
замечанию |
п.4, |
|
этот максимум |
функции |
||||||||||||
является ее наибольшим значением. Итак, коробка имеет наибольший объем, если сторона вырезанного квадрата равна a 6 .
6 .
Рис. 11 Рис. 12
Пример 5. Найти высоту цилиндра наибольшего объема, который можно вписать в данный прямой конус (рис.12).
Решение. |
Пусть |
высота конуса |
OB |
h |
и радиус |
|
основания конуса OA |
R . Высоту цилиндра |
OC обозначим |
||||
через |
y , а радиус основания OF - через |
x . Объем цилиндра |
||||
V |
x2 y . В |
данном |
случае объем V |
зависит |
от двух |
|
24

переменных x и y . Однако можно составить уравнение, связывающее эти переменные.
Из подобия треугольников AOB и DCB находим
DC : CB OA : OB , или x : (h y) R : h .
Отсюда x R(h y) h . Подставляя это выражение x в формулу для вычисления объема цилиндра, получаем
h . Подставляя это выражение x в формулу для вычисления объема цилиндра, получаем
V |
R2 |
(h y)2 y . |
|
h2 |
|||
|
|
Очевидно, что переменная y может принимать значения от 0
до h . Найдем наибольшее значение этой функции в интервале
(0, h) .
Находим производную от функции V по переменной y :
V |
R2 |
(h2 |
4hy 3y 2 ) . |
|
h2 |
||||
|
|
|
Приравниваем производную нулю и находим критическую точку в интервале (0, h) :
h2 4hy 3y2 ; |
y |
h 3 |
|
|
|
1 |
|
|
|
(точка y2 h интервалу (0, h) не принадлежит). |
||||
|
|
R2 |
|
|
Так как вторая производная |
V |
|
( |
4h 6 y) в точке |
h2 |
||||
h 3 отрицательна, то при y h 3 объем V |
имеет максимум. |
|||
Это максимальное значение является наибольшим.
6. Направление выпуклости и точки перегиба графика функции. Пусть функция y  f (x) дифференцируема на
f (x) дифференцируема на
интервале (a,b) . Тогда существует касательная к графику
функции y |
f (x) в любой точке M (x; f (x)) |
этого |
графика ( |
a x b ), |
причем касательная не параллельна |
оси Оу, |
|
поскольку ее угловой коэффициент, равный f |
(x) , конечен. |
||
25

Определение 1. Будем говорить, что график функции имеет на (a,b) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (a,b) (рис. 13).
Рис. 13
Теорема 11. Если функция y  f (x) имеет на интервале
f (x) имеет на интервале
(a,b) вторую производную и f |
(x) |
0 ( f |
(x) 0) во всех |
точках (a,b) , то график функции |
y |
f (x) |
имеет на (a,b) |
выпуклость, направленную вниз (вверх).
Определение 2. Точка М( x0 ; f (x0 ) ) называется точкой перегиба графика функции y  f (x) , если в точке М график имеет касательную, и существует такая окрестность точки x0 , в пределах которой график функции y
f (x) , если в точке М график имеет касательную, и существует такая окрестность точки x0 , в пределах которой график функции y  f (x) слева и справа от точки x0 имеет разные направления выпуклости.
f (x) слева и справа от точки x0 имеет разные направления выпуклости.
Очевидно, что в точке перегиба касательная пересекает график функции, так как с одной стороны от этой точки график лежит под касательной, а с другой – над нею, т.е. в окрестности точки перегиба график функции геометрически переходит с одной стороны касательной на другую и «перегибается» через неё. Отсюда произошло название «точка перегиба» (рис. 14).
26

Рис. 14
Теорема 12(необходимое условие точки перегиба). Пусть график функции y  f (x) имеет перегиб в точке М( x0 ; f (x0 )
f (x) имеет перегиб в точке М( x0 ; f (x0 )
) и пусть функция y |
f (x) |
имеет в точке |
x0 |
непрерывную |
||||
вторую производную. Тогда |
f |
(x) в точке |
x0 |
обращается в |
||||
нуль, т.е. f (x0 ) |
0 . |
|
|
|
|
|
|
|
Следует заметить, что не всякая точка М( x0 ; f (x0 ) ), для |
||||||||
которой f (x0 ) |
0 , является точкой перегиба. |
|
||||||
Например, график функции |
f (x) |
x4 не имеет перегиба в |
||||||
точке (0; 0), хотя |
f (x) |
12x2 |
0 |
при |
x 0 (рис. 15). |
|||
Поэтому |
равенство |
|
нулю |
второй |
производной |
|||
является лишь необходимым условием перегиба.
Точки М( x0 ; f (x0 ) ) графика, для которых f  (x0 ) 0 , будем называть критическими.
(x0 ) 0 , будем называть критическими.
Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке, для чего следует установить достаточное условие перегиба.
27

Рис. 15 |
Рис. 16 |
|
Теорема 13 (достаточное условие точки перегиба). Пусть
функция y |
f (x) имеет вторую производную в некоторой |
|||
окрестности |
точки |
x0 . |
Тогда, если в пределах указанной |
|
окрестности |
f (x) |
имеет разные знаки слева и справа от |
||
точки x0 , то график |
y |
f (x) имеет перегиб в точке М( |
||
x0 ; f (x0 ) ). |
|
|
|
|
З а м е ч а н и е. |
Теорема остается верной, если f (x) |
|||
имеет вторую производную в некоторой окрестности точки x0 , за исключением самой точки x0 , и существует касательная к
графику функции в точке М. Тогда, если в пределах указанной окрестности f  (x) имеет разные знаки слева и справа от точки
(x) имеет разные знаки слева и справа от точки
x0 , то график функции |
y |
f (x) имеет перегиб в точке М( |
|||
x0 ; f (x0 ) ). |
|
|
|
|
|
Рассмотрим пример: |
|
f (x) |
x1/ 3 . Эта функция в точке |
||
x 0 имеет |
бесконечную |
производную, а касательная к |
|||
графику функции в точке О(0; 0) |
совпадает с осью Оу. Вторая |
||||
производная |
в |
точке x |
0 |
не существует. Однако график |
|
функции y |
x1/ 3 |
имеет перегиб в точке O(0;0) , так как вторая |
|||
28
производная f (x) |
2 /(9x5 / 3 ) имеет слева и справа от точки |
x 0 разные знаки (рис. 16). |
|
Итак, вопрос о |
направленности выпуклости и точках |
перегиба графика функции исследуется с помощью второй производной.
В качестве примера возьмем функцию f (x) x3 3x,
которую начали рассматривать в п.2. Знак второй производной будем отмечать на вспомогательном чертеже, изображенном на рис.10. Находим вторую производную: f  (x) 6x. Из уравнения 6х = 0 получаем одну критическую
(x) 6x. Из уравнения 6х = 0 получаем одну критическую
точку: O(0;0) . Отметив точку |
|
x |
0 |
на вспомогательном |
чертеже (рис. 17) и определив знак |
f |
(x) в ее окрестности, |
||
получаем: слева от точки x 0 |
f |
(x) <0 (выпуклость графика |
||
направлена вверх), а справа |
f |
(x) >0 |
(выпуклость графика |
|
направлена вниз), т.е. точка O(0;0) является точкой перегиба
графика рассматриваемой функции. Этот график схематически изображен на рис. 18.
Рис. 17
7. Асимптоты графика функции. При исследовании поведения функции на бесконечности, т. е. при х  и при х
и при х или вблизи точек разрыва второго рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называют
или вблизи точек разрыва второго рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называют
29
