
Избранные главы математики. Бырдин А.П., Заварзин Н.В
.pdf
А.П. Бырдин Н.В. Заварзин А.А. Сидоренко Л.П. Цуканова
ИЗБРАННЫЕ ГЛАВЫ МАТЕМАТИКИ
Часть 2
Учебное пособие
|
|
|
|
|
|
divFdV |
FndS |
||||
V |
S |
||||
Воронеж 2012
ФГБОУ ВПО “Воронежский государственный технический университет”
А.П. Бырдин Н.В. Заварзин А.А. Сидоренко Л.П. Цуканова
ИЗБРАННЫЕ ГЛАВЫ МАТЕМАТИКИ
Часть 2
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Воронеж 2012
1

УДК 517.2 |
|
Избранные главы математики: учеб. пособие |
/ |
А.П. Бырдин, Н.В. Заварзин, А.А. Сидоренко, Л.П. Цуканова.
Воронеж: ФГБОУ ВПО “Воронежский |
государственный |
|
технический университет”, 2012. Ч.2. 236 |
с. |
|
В учебном пособии излагаются |
элементы высшей |
|
математики. Теоретический материал |
иллюстрируется |
|
большим количеством примеров. Имеются задачи для самостоятельного решения и типовых расчетов.
Издание соответствует |
требованиям Федерального |
|||
государственного |
образовательного |
стандарта |
высшего |
|
профессионального |
образования |
по |
специальности |
160700 |
«Проектирование авиационных и ракетных двигателей», дисциплине ”Математика”.
Предназначено для студентов очной формы обучения. Учебное пособие подготовлено в электронном виде в
текстовом редакторе Word 2003 и содержится в файле РД-Математика-Часть2.pdf.
Ил. 63. Библиогр.: 8 назв.
Научный редактор д-р физ.-мат. наук, проф. В.Д. Репников
Рецензенты: кафедра математического моделирования Воронежского государственного университета (зав. кафедрой д-р физ.-мат. наук, проф. В.А. Костин); канд. техн. наук, доц. А.В. Паринов
Бырдин А.П., Заварзин Н.В., Сидоренко А.А., Цуканова Л.П., 2012
Оформление. ФГБОУ ВПО “Воронежский государственный технический университет”, 2012
2
ВВЕДЕНИЕ
Данное пособие представляет собой обработку курса лекций, которые авторы на протяжении ряда лет читали студентам очного обучения специальности «Ракетные двигатели» Воронежского государственного технического университета. Пособие написано в соответствии с программой курса “Высшая математика” и может быть использовано студентами других специальностей.
В учебном пособии представлен материал, который изучается во втором семестре, это – приложения дифференциального исчисления к исследованию функций, неопределенные и определенные интегралы, функции нескольких переменных. Цель работы – помочь студентам усвоить и закрепить основные положения исследования функций с помощью дифференциального исчисления и построения их графиков, методы интегрирования, вычисления и приложения определенных и несобственных интегралов.
При написании учебного пособия авторы стремились изложить материал по возможности полно, строго и доступно. Представленная работа направлена на совершенствование учебного процесса и способствует целенаправленному использованию знаний математики.
По каждому разделу приведены примеры решения задач, а также многочисленные задачи для контроля усвоения материала. Ко всем рекомендуемым для самостоятельного решения задачам приведены ответы. Поэтому представленное учебное пособие может быть использовано преподавателями для проведения практических занятий. Пособие содержит четыре главы, включающие индивидуальные задания.
3
1. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
1.1. Основные теоремы дифференциального исчисления Теорема 1 (теорема Ферма). Пусть функция
определена на интервале (a,b) и в некоторой точке x0 этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке x0 существует производная, то она равна нулю,
т. е. f (x0 ) 0.
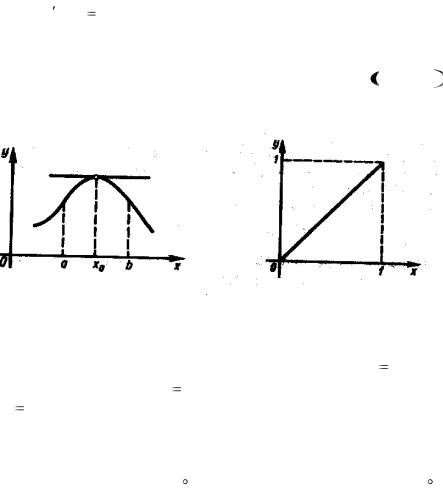
Геометрический смысл теоремы Ферма состоит в том, что если в точке x0 дифференцируемая функция f (x) имеет
наибольшее или наименьшее значение, то в точке x0 ; f (x0 ) касательная к графику функции f (x) параллельна оси Ox
(рис. 1).
Рис. 1 |
Рис. 2 |
|
З а м е ч а н и е. Теорема неверна, если функцию |
f (x) |
|
рассматривать на отрезке |
[a,b] . Так функция f (x) x |
на |
отрезке [0,1] в точке x |
0 принимает наименьшее, а в точке |
|
x 1 – наибольшее значение, однако как в той, так и в другой точке производная в нуль не обращается, а равна единице
(рис. 2).
Теорема 2 (теорема Ролля). Пусть на [a,b] определена функция f (x) , причем: 1 ) f (x) непрерывна на [a,b] ; 2 )
4
f (x) дифференцируема на (a,b) ; 3 ) |
f (a) f (b) . Тогда |
существует точка c a,b , в которой |
f (c) 0 . |
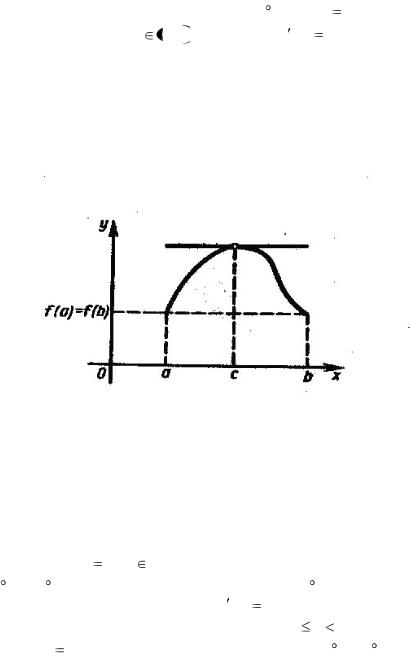
Геометрически теорема Ролля означает, что у графика непрерывной на отрезке [a,b] и дифференцируемой внутри этого отрезка функции, принимающей на его концах равные
значения, существует точка (c; f (c)) , в которой |
касательная |
параллельна оси Ох (рис. 3). На рис. 3 в точке |
с функция |
f (x) принимает наибольшее значение. |
|
Рис. 3
Следует отметить, что все три условия теоремы Ролля существенны. Чтобы убедиться в этом, достаточно привести примеры функций, для которых выполнялись бы два условия теоремы, а третье не выполнялось и производные которых не обращались бы в нуль ни в одной точке. Так, например,
функция |
f (x) x , x [0,1] (см. рис. 2) удовлетворяет условиям |
|||||
1 и |
2 , |
но не удовлетворяет |
условию 3 |
и |
для нее не |
|
существует точки с такой, что f |
(c) |
0 . Рассмотрим еще два |
||||
примера. |
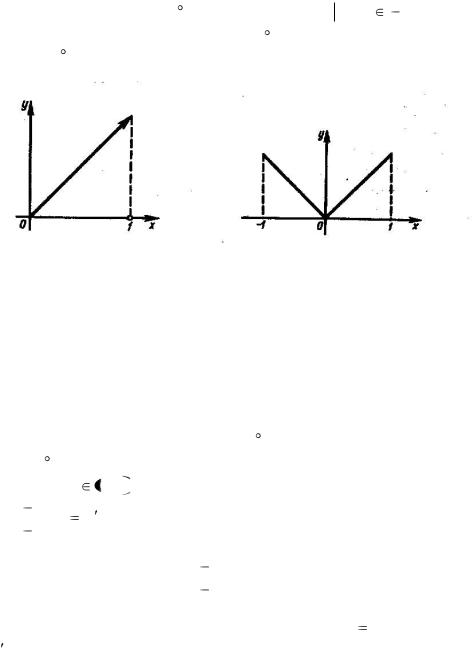
Функция f (x) , равная |
x, |
если 0 |
x |
1, и равная 0, |
|
если |
x |
1 (рис.4), удовлетворяет |
условиям 2 |
и 3 , но не |
||
5
удовлетворяет условию 1 . Функция f (x) 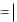 x , x [ 1,1]
x , x [ 1,1]
(рис. 5) удовлетворяет условиям 1 и 3 , но не удовлетворяет условию 2 . Для этих функций также не существует точки, в которой их производная обращалась бы в нуль.
и 3 , но не удовлетворяет условию 2 . Для этих функций также не существует точки, в которой их производная обращалась бы в нуль.
Рис. 4 Рис. 5
Отметим, что в математике существенность тех или иных условий доказываемых теорем проверяется построением соответствующих примеров, когда невыполнение того или иного условия теоремы приводит к тому, что утверждение теоремы становится неверным.
Теорема 3 (теорема Лагранжа). Пусть на
определена функция |
f (x) , причем: 1 |
) f (x) |
непрерывна на |
||||||||
[a,b]; |
2 ) |
f (x) |
дифференцируема на (a,b) . Тогда существует |
||||||||
точка |
|
c |
a, b |
такая, |
что |
справедлива |
формула |
||||
|
f (b) |
f (a) |
f (c). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
b |
a |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
Установим |
геометрический смысл теоремы Лагранжа |
|||||||||
(рис.6). |
Величина |
|
f (b) |
f (a) |
является |
угловым |
|||||
|
|
|
|
||||||||
|
b |
a |
|||||||||
|
|
|
|
|
|
|
|
|
|||
коэффициентом |
секущей, |
проходящей |
через |
точки |
|||||||
M1 (a; f (a)) и |
M 2 (b; f (b)) графика |
функции |
y |
f (x), а |
|||||||
f (c)  угловой коэффициент касательной к графику в точке
угловой коэффициент касательной к графику в точке
6
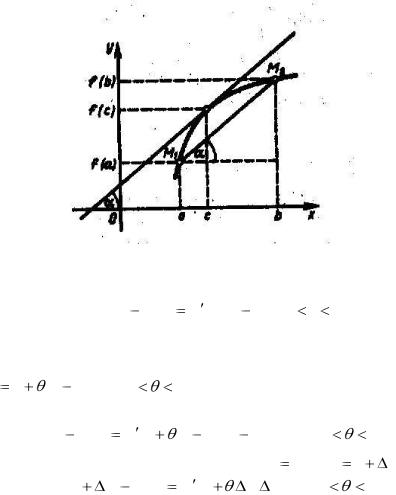
(c; f (c)). Из теоремы Лагранжа следует, что существует точка
с такая, что касательная к графику в точке |
(c; f (c)) |
параллельна секущей M1M 2. Таких точек может быть и несколько, но, по крайней мере, одна всегда существует.
Рис. 6 |
|
З а м е ч а н и е 1. Равенство |
|
f (b) f (a) f (c) (b a), a c b, |
(1.1) |
называется формулой Лагранжа или формулой конечных приращений.
З а м е ч а н и е 2. Так как точка с лежит между a и b, то
c a |
(b a) , где 0 |
|
1. Учитывая это, формулу Лагранжа |
|||||
можно записать в виде |
|
|
|
|
|
|||
f (b) |
f (a) f (a |
(b a))(b |
a), |
где 0 |
1. |
|
||
З а м е ч а н и е |
3. Если положить a |
x, b |
x |
x, то |
||||
получим |
f (x |
x) |
f (x) |
f (x |
x) x, |
где 0 |
1. |
Такая |
запись формулы Лагранжа часто бывает удобнее, чем запись в виде (1.1).
7

Как будет показано в дальнейшем, теорема Лагранжа лежит в основе доказательства многих формул и теорем
анализа. |
|
|
|
|
|
|
Теорема 4 (теорема Коши). Пусть функции |
f (x) и |
|||||
g(x) непрерывны на [a,b] и дифференцируемы на |
(a,b) . |
|||||
Пусть, |
кроме того, g (x) |
0. Тогда существует |
точка |
|||
c (a,b) |
такая, что справедлива формула |
|
||||
|
|
f (b) f (a) |
|
f (c) |
. |
(1.2) |
|
|
|
|
|||
|
|
g(b) g(a) |
|
g (c) |
|
|
З а м е ч а н и е. Формула (2) называется формулой Коши
или обобщенной формулой конечных приращений.
1.2. Раскрытие неопределенностей. Правило Лопиталя
1. |
Раскрытие неопределенности вида |
0 |
. |
Будем |
||||||||
0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
говорить, что отношение двух функций |
|
f (x) |
при x |
a есть |
||||||||
|
g(x) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
неопределенность вида |
0 |
, если |
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
lim |
f (x) lim g(x) |
0. |
|
|
|
|
|||
|
|
|
x |
a |
x a |
|
|
|
|
|
|
|
Раскрыть эту неопределенность – значит вычислить |
||||||||||||
предел |
lim |
f (x) |
, если он существует, |
или установить, что он |
||||||||
|
||||||||||||
|
x a |
g(x) |
|
|
|
|
|
|
|
|
||
не существует. Следующая теорема устанавливает правило для раскрытия неопределенности вида 00 .
Теорема 5 (теорема Лопиталя). Пусть функции f (x) и g(x) определены и дифференцируемы в некоторой окрестности точки а, за исключением, быть может, самой
8

точки |
а. |
Пусть, |
далее, |
|
lim f (x) |
|
lim g(x) |
0 |
|
и g (x) |
0 в |
|||||||
|
|
|
|
|
x a |
|
|
x |
a |
|
|
|
|
|
|
|
||
указанной |
окрестности |
точки |
а. |
Тогда, |
если |
существует |
||||||||||||
предел |
отношения |
производных |
lim |
|
f (x) |
|
(конечный |
или |
||||||||||
|
g (x) |
|||||||||||||||||
|
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|||
бесконечный), то |
существует |
и |
предел |
lim |
|
f (x) |
, причем |
|||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
a |
g(x) |
|
|||
справедлива формула lim |
|
f (x) |
lim |
f (x) |
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x a |
|
g(x) |
x a |
g (x) |
|
|
|
|
|
|
|
|
|
||
Эту теорему обычно называют правилом Лопиталя. |
|
|||||||||||||||||
З а м е ч а н и е |
1. Если производные |
f (x) и g (x) |
||||||||||||||||
удовлетворяют тем же требованиям, что и сами функции |
f (x) |
|||||||||||||||||
и g(x) , то правило Лопиталя можно применить повторно. При этом получаем
lim |
f (x) |
lim |
f (x) |
lim |
f (x) |
. |
|
|
|
||||
x a |
g(x) |
x a |
g (x) |
x a |
g (x) |
|
З а м е ч а н и е 2. |
|
Теорема остается верной и в случае, |
||||||||||||||||||||||||||||||||
когда x |
, |
x |
|
|
|
|
и |
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Р а с с м о т р и м п р и м е р ы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1. lim |
1 |
cos x |
lim |
sin x |
|
1 |
lim |
sin x |
|
|
1 |
|
1 |
|
|
1 |
. |
|
|
|||||||||||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x 0 |
|
|
|
|
x 0 2x |
|
2 x 0 |
|
x |
2 |
|
|
|
|
2 |
|
|
|
||||||||||||||||
2. lim |
x |
|
sin x |
|
lim |
1 |
|
cos x |
|
lim |
sin x |
|
|
1 |
lim |
sin x |
|
1 |
|
1 |
1 |
. |
||||||||||||
|
|
x3 |
|
|
3x2 |
|
|
|
|
|
|
|
||||||||||||||||||||||
x 0 |
|
x 0 |
|
|
|
x 0 6x |
|
6 x 0 |
x |
6 |
|
|
|
6 |
|
|||||||||||||||||||
3. lim |
e x |
1 |
|
lim |
e x |
|
lim e x 1. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x 0 |
|
|
x |
|
x |
0 |
1 |
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
9
