681

УДК 519.872.8

Д.Л. Деревянкин, А.Р. Давыдов

Пермский национальный исследовательский политехнический университет, Пермь, Россия

РАЗРАБОТКА ИМИТАЦИОННОЙ МОДЕЛИ ЛОГИСТИЧЕСКОЙ СИСТЕМЫ МАШИНОСТРОИТЕЛЬНОГО ПРЕДПРИЯТИЯ

Изложены основные этапы разработки имитационной модели процесса движения конструкторской документации на предприятии. Проведен анализ функционирования существующей системы, собраны и обработаны необходимые данные о её работе. Построена математическая модель, которая впоследствии была реализована с использованием статистического моделирования на ЭВМ. На основе полученных результатов сделаны выводы и даны рекомендации по улучшению существующей системы. Работа носит исследовательский характер и имеет важное прикладное значение.

Ключевые слова: система массового обслуживания, имитационное моделирование, логистическая система предприятия, статистический анализ.

D.L. Derevyankin, A.R. Davydov

Perm National Research Polytechnic University, Perm, Russia

DEVELOPMENT OF SIMULATION MODEL OF LOGISTIC

SYSTEM OF ENGINEERING ENTERPRISE

The basic stages of the development of simulation model of motion process of design documentation in the enterprise are stated. Functioning of the existing system is analyzed, necessary information about working of this system is collected and processed. The mathematical model is carried out and realized on computer with using of statistical modeling. Based on these results conclusions are drawn and recommendations on improving of the existing system are given. The work is research character and has great practical importance.

Keywords: queuing system, simulationmodeling, logistic system of the enterprise, statistical analysis.

1. Формулирование и построение математической модели

Для успешной деятельности предприятия необходимо эффективное функционирование всех его внутренних систем. Одной из таких важных систем является система движения конструкторской документации. В данной работе эта система рассматривается через призму тео-

31

рии массового обслуживания, на основе которой создается имитационная модель. Уникальность работы заключается в применении теории массового обслуживания и имитационного моделирования к процессу движения конструкторской документации на предприятии.

Основным элементом конструкторской документации является пакет данных – совокупность чертежей и дополнительной информации по какому-либо изделию или детали изделия. Все данные, которые поступают на предприятие, можно разделить на четыре группы:

•документация, поступающая в электронном виде от сторонних организаций;

•документация, поступающая в бумажном виде от сторонних организаций;

•документация, состоящая из 3D-моделей;

•документация собственной разработки.

Такое разделение обусловлено тем, что по каждому из этих видов работает отдельное бюро в отделе главного конструктора.

Документация, поступившая от сторонних организаций, обрабатывается в отделе стандартизации и документации (ОСиД), где происходят её переработка под стандарты предприятия и преобразование в электронный вид. После этого документация поступает в отдел главного конструктора, где происходят её проверка и дополнительная обработка. На последнем этапе обработанная и проверенная документация поступает в бюро ведущих технологов, которые расписывают технологию производства изделия, описанного в данной документации. И уже в соответствии с этой технологией цеха начинают производство изделия. Документация, которая была разработана на предприятии, в проектном центре, поступает в ОСиД, после чего идет непосредственно в бюро ведущих технологов, минуя отдел главного конструктора.

Требуется разработать имитационную модель, которая бы с высокой точностью отражала существующую систему движения конструкторской документации на предприятии, произвести анализ полученной модели.

Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы. Эта информация определяет основную цель моделирования системы и позволяет сформулировать требования кразрабатываемой математической модели.

32

Математическую схему [1] можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды, т.е. имеет место цепочка «описательная модель – математическая схема – математическая модель».

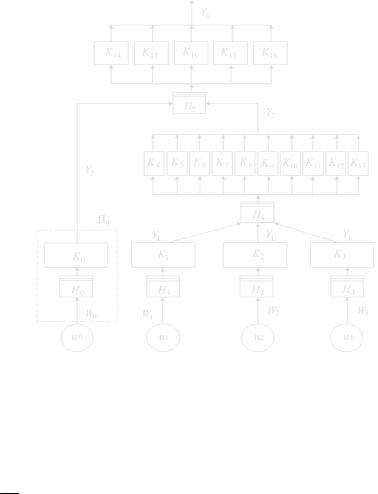
Процесс движения конструкторской документации на данном предприятии с математической точки зрения можно представить в виде сети массового обслуживания. Далее строится Q-схема (рис. 1) данного процесса и определяются все параметры и характеристики, необходимые для построения имитационной модели.

Рис. 1. Q-схема движения конструкторской документации на предприятии

Поступление пакетов конструкторской документации (поток заявокw0 ,w1,w2 ,w3 W ), т.е. интервалы времени между моментами приходов пакетов с данными (вызывающие моменты), на входе каналов Ki , i =0,3, образует подмножество неуправляемых переменных. В свою очередь поток обслуживания пакетов отделом стандартизации и доку-

33

ментации (ОСиД) u0 ,u1,u2 ,u3 U , т.е. интервалы времени между нача-

лом и окончанием обработки пакета данных, образует подмножество управляемых переменных.

Данные, обслуженные каналами K1, K2 , K3 , образуют выходной поток y1 Y (т.е. интервалы времени между моментами окончания об-

служивания пакетов данных образуют подмножество выходных переменных), который является входным потоком для обслуживания в отделе главного конструктора. Вместе с тем обслуживание пакетов отделом главного конструктора u4 ,u5 ,...,u13 U т.е. интервалы времени ме-

жду началом и окончанием обработки пакета данных, образует подмножество управляемых переменных.

Данные, обслуженные каналами K4 ,..., K13 , а также каналом K0 , образуют выходной поток y2 Y (т.е. интервалы времени между мо-

ментами окончания обслуживания пакетов данных образуют подмножество выходных переменных), который является входным потоком для обслуживания пакетов данных ведущими технологами. А поток обслуживания данных ведущими технологами u14 ,u15 ,...,u18 U также

образует подмножество управляемых переменных.

Для входящих потоков w0 , w1, w2 , w3 W выполняются условия ординарности и ограниченного последействия, но не выполняется условие стационарности, для y1, y2 выполняется условие стационарно-

сти, но не выполняются условия ординарности и ограниченного последействия, так как моменты поступления уже являются зависимыми. Для потоков обслуживания u0 ,u1,...,u18 U выполняются условия ста-

ционарности, ординарности и ограниченного последействия. Оператор сопряжения элементов структуры R: в данной системе

сначала пакеты данных обслуживают параллельно четыре бюро из отдела ОСиД (каналы K0 , K1, K2 , K3 ), а затем первоначально обработанная документация поступает в бюро из отдела главного конструктора ( K4 , ..., K13 ). После проверки данные из отдела главного конструктора

поступают к ведущим технологам, после чего направляются в цеха. Таким образом, имеет место многофазное многоканальное обслуживание (многофазная многоканальная Q-схема). Предполагается, что обратная связь отсутствует и имеет место разомкнутая Q-схема.

34

Опишем совокупность собственных параметров Q-схемы: Имеются девятнадцать каналов обслуживания, сгруппированные

в три фазы обслуживания.

Q-схема имеет шесть накопителей. Емкость всех накопителей – бесконечная ( LHi →∞,i =1,6 ), т.е. эта система является системой с

ожиданием.

Совокупность состояний системы Z описывается векторами со- ur

стояний zi = (ziH , ziK ) , где ziH – число пакетов в очереди (состояние накопителя Hi ); ziK – состояния отделов ОСиД, ГК, ВТ (состояние кана-

ла Ki ), i = 0, 1, 2, 3…18.

Оператор алгоритма функционирования Q-схемы: бесприоритетное и беспрерывное обслуживание.

2. Получение и обработка статистических данных

Источником получения данных для моделирования движения конструкторской документации были электронные метки времени движения пакетов с конструкторской документацией. В результате сбора данных были получены входные статистические совокупности.

На первом этапе получен статистический материал (23 статистические совокупности), который был преобразован в удобный для анализа вид.

Предположим, что в нашем распоряжении результаты наблюдений над непрерывной случайной величиной Х, оформленные в виде простой статистической совокупности. Разделим весь диапазон наблюденных значений Х на интервалы, или «разряды», и подсчитаем количество значений mi , приходящееся на каждый i-й разряд. Это число

разделим на общее число наблюдений n и найдем частоту, соответствующую данному разряду [2]:

Сумма частот всех разрядов, очевидно, должна быть равна еди-

нице.

В результате преобразования исходных данных к удобному для анализа виду были получены следующие статистические ряды, оформ-

35

ленные в виде таблиц, в которых приведены разряды в порядке их расположения вдоль оси абсцисс и соответствующие частоты.

За Ii обозначаются интервалы значений: mi – число наблюдений в данном интервале, pi* – соответствующие частоты.

Статистический ряд часто оформляется графически в виде так называемой гистограммы [2].

Рассмотрим группировку данных на примере продолжительности обработки пакетов данных в одном из бюро отдела стандартизации и документации (ОСиД). Это бюро работает с электронной документацией, содержащей 3D-модели (табл. 1).

Таблица 1 Абсолютные и относительные частоты статистического распределения

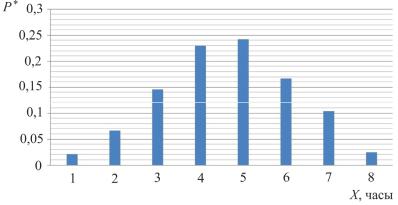
Гистограмма для данного статистического ряда представлена на рис. 2.

Рис. 2. Гистограмма распределения частот статистического ряда

Для каждой числовой характеристики случайной величины Х существует ее статистическая аналогия. Для основной характеристики положения – математического ожидания случайной величины – такой аналогией является среднеарифметическое полученных значений случайной величины:

36

n

∑xi

где xi – значение случайной величины, наблюдаемое в i-м опыте; n –

число опытов. Эту характеристику мы будем в дальнейшем называть статистическим средним случайной величины.

Согласно закону больших чисел [2] при неограниченном увеличении числа опытов статистическое среднее приближается (сходится по вероятности) к математическому ожиданию. При достаточно большом значении n статистическое среднее может быть принято приближенно равным математическому ожиданию.

Подобные статистические аналогии существуют для всех числовых характеристик. Условимся в дальнейшем эти статистические аналогии обозначать теми же буквами, что и соответствующие числовые характеристики, но снабжать их значком *.

Рассмотрим, например, дисперсию случайной величины. Она представляет собой математическое ожидание случайной величины

X 2 = ( X − mx )2 :

Если в этом выражении заменить математическое ожидание его статистической аналогией – среднеарифметическим, мы получим статистическую оценку дисперсии случайной величины Х:

ются статистические начальные и центральные моменты любых порядков.

При увеличении числа наблюдений, очевидно, все статистические характеристики будут сходиться по вероятности к соответствующим математическим характеристикам и при достаточном n могут быть приняты приближенно равными им.

При очень большом количестве опытов вычисление характеристик по формулам (2)–(4) становится чрезмерно громоздким, и можно

37

применить следующий прием: воспользоваться теми же разрядами, на которые был расклассифицирован статистический материал для построения статистического ряда или гистограммы, и считать приближенно значение случайной величины в каждом разряде постоянным и равным среднему значению, которое выступает в роли «представителя разряда». Тогда статистические числовые характеристики будут выражаться приближенными формулами [2]:

число разрядов.

Во всяком статистическом распределении неизбежно присутствуют элементы случайности. Только при очень большом числе наблюдений эти элементы случайности сглаживаются, и случайное явление обнаруживает в полной мере присущую ему закономерность. На практике мы почти никогда не сталкиваемся с таким большим числом наблюдений и вынуждены считаться с тем, что любому статистическому распределению свойственны в большей или меньшей мере черты случайности. Поэтому при обработке статистического материала часто приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую лишь существенные черты статистического материала, но не случайности, связанные с недостаточным объемом экспериментальных данных. Такая задача называется задачей выравнивания (сглаживания) статистических рядов.

38

Задача выравнивания [2] заключается в том, чтобы подобрать теоретическую плавную кривую распределения, с той или иной точки зрения наилучшим образом описывающую данное статистическое распределение.

Как правило, принципиальный вид теоретической кривой выбирается заранее из соображений, связанных с существом задачи, а в некоторых случаях просто с внешним видом статистического распределения. Аналитическое выражение выбранной кривой распределения зависит от некоторых параметров; задача выравнивания статистического ряда переходит в задачу рационального выбора тех значений параметров, при которых соответствие между статистическим и теоретическим распределениями оказывается наилучшим.

Следует иметь в виду, что любая аналитическая функция f (x), с помощью которой выравнивается статистическое распределение, должна обладать основными свойствами плотности распределения:

Выровняем статистическое распределение продолжительности обработки пакетов данных в одном из бюро отдела стандартизации и документации с помощью нормального распределения:

Нормальный закон зависит от двух параметров – т и σ. Подберем эти параметры так, чтобы сохранить первые два момента – математическое ожидание и дисперсию статистического распределения.

Вычислим приближенно статистическое среднее промежутков времени в совокупностях по формуле (5), причем за представителя каждого разряда примем его середину. Дисперсию вычислим по формуле (6).

Выберем параметры m и σ нормального закона так, чтобы выполнялись условия:

m = m*x , σ2 = DX* .

Запишем полученные параметры и получившиеся законы распределения:

39

Таким образом, были подобраны теоретические распределения для всех имеющихся статистических совокупностей.

Рассмотрим вопрос о согласованности теоретического и статистического распределений.

Допустим, что данное статистическое распределение выровнено с помощью некоторой теоретической кривой f (x). Как бы хорошо ни была подобрана теоретическая кривая, между нею и статистическим распределением неизбежны некоторые расхождения. Естественно, возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что подобранная нами кривая плохо выравнивает данное статистическое распределение. Для ответа на такой вопрос используют так называемые «критерии согласия». Один из наиболее часто применяемых критериев согласия – так называемый «критерий χ2 » Пирсона [2].

Схема применения критерия χ2 к оценке согласованности теоретического и статистического распределений сводится к следующему:

1. Определяется мера расхождения χ2 по формуле

где ni* – число опытных данных попавших в i-й интервал; ni – теоретическое число попавших в i-й интервал.

2.Определяется число степеней свободы r как число разрядов k минус число наложенных связей s: r = k −s .

3.По r и χ2 с помощью табл. 4 приложения [2] определяется ве-

роятность того, что величина, имеющая распределение χ2 с r степенями свободы, превзойдет данное значение χ2 .

Если эта вероятность весьма мала, гипотеза отбрасывается как неправдоподобная. Если эта вероятность относительно велика, гипотезу можно признать не противоречащей опытным данным.

40