681

χ = у′′(х)= − Р1 М′′.

Окончательно дифференциальное уравнение примет вид

ЕРтI т′′+χ%(т)= 0,

а с учетом формулы Энгессера – Шенли [7]

l2 Р0 т′′+χ%(т)= 0, π2 Р

где m, χ%, – безразмерные величины, полученные из выражений (13),

m = ∆MP r ; χ% = Em∆πPd 2δχ.

В табл. 4 приведены значения критической силы, вычисленной по касательному модулю для двух стержней, значения вертикального перемещения конца стержня и максимальный прогиб при s = l/2. Поскольку критическая сила для стержней малой гибкости существенно больше, чем у гибких стержней, то и перемещения, особенно продольные, также больше, а вот поперечные перемещения отличаются незначительно.

Рис. 6. Зависимость величины поперечного перемещения сечения s = l/2 в стержнях 3 и 4

191

На рис. 6 показано изменение поперечного перемещения от приложенной продольной силы. Видно, что при Р=Р0 прогиб первоначально прямого стержня равен нулю, а затем резко возрастает. Фактически за момент потери устойчивости принимается момент, когда прогиб достигает некоторой достаточно большой величины, но значения силы при этом настолько большие, что напряжения превосходят предельные значения. Таким образом, негибкие стержни можно рассчитывать только на прочность.

Библиографический список

1.Попов Е.П. Теория и расчет гибких упругих стержней. – М.:

Наука, 1986. – 296 с.

2.Кузнецов В.В., Левяков С.В. О вторичной потере устойчивости Эйлерова стержня // Прикладная математика и техническая физика. – 1999. – Т. 40, № 6. – С. 184–185.

3.Левяков С.В. Формы равновесия и вторичная потеря устойчивости прямого стержня, нагруженного продольной силой // ПМТФ. – 2001. – Т. 42, № 2. – С. 153–159.

4.Бартоломей М.Л., Труфанов Н.А., Шардаков И.Н. Численный анализ устойчивости многоэлементной стержневой конструкции при непропорциональном нагружении // Вычислительная механика сплош-

ных сред. – 2012. – Т. 5, № 1. – С. 25–32.

5.Писаренко Г.С. Сопротивление материалов. – Киев: Вища шк., 1986. – 775 с.

6.Третьяков А.В., Зюзин В.И. Механические свойства металлов и сплавов при обработке давлением. – М.: Металлургия, 1973. – 224 с.

7.Работнов Ю.Н. Механика деформируемого твердого тела. – М.:

Наука, 1988. – 712 с.

References

1.Popov E.P. Teorija i raschet gibkih uprugih sterzhnej [Theory and design of flexible elastic rods]. Moscow, Nauka, 1986, 296 p.

2.Kuznecov V.V., Levjakov S.V. O vtorichnoj potere ustojchivosti Jejlerova sterzhnja [On the secondary loss of stability of Euler rod]. Prikladnaja matematika i tekhnicheskaja fizika, 1999, vol. 40, no. 6, pp 184–185.

3.Levjakov S.V. Formy ravnovesija i vtorichnaja poterja ustojchivosti prjamogo sterzhnja, nagruzhennogo prodol'noj siloj [Equilibrium forms and secondary loss of stability of a straight rod with longitudinal force loading]. rod]. Prikladnaja matematika i tekhnicheskaja fizika, 2001, vol. 42, no. 2, pp 153–159.

192

4.Bartolomej M.L., Trufanov N.A., Shardakov I.N. Chislennyj analiz ustojchivosti mnogojelementnoj sterzhnevoj konstrukcii pri neproporcional'nom nagruzhenii [Numerical analysis of the stability of the multiple-rod structure with non-proportional loading]. Vychislitel'naja mehanika sploshnyh sred, 2012, vol. 5, no. 1, pp 25–32.

5.Pisarenko G.S. Soprotivlenie materialov [Strength of materials]. Kiev: Vissha shkola, 1986, 775 p.

6.Tret'jakov A.V., Zjuzin V.I. Mehanicheskie svojstva metallov i splavov pri obrabotke davleniem. Spravochnik. [Mechanical properties of metals and alloys under pressure treatment. Directory]. Moscow: Metallurgija, 1973, 224 p.

7.Rabotnov Ju.N. Mehanika deformiruemogo tverdogo tela [Fracture Mechanics]. Moscow: Nauka, 1988, 712 p.

Получено 27.09.2012

Об авторах

Суходоева Алла Алексеевна (Пермь, Россия) – кандидат тех-

нических наук, доцент кафедры вычислительной математики и механики Пермского национального исследовательского политехнического университета (614990, г. Пермь, Комсомольский пр., 29, e-mail: sukhodoeva@ya.ru).

Тихомирова Ксения Алексеевна (Пермь, Россия) – студентка кафедры динамики и прочности машин Пермского национального исследовательского политехнического университета (614990, г. Пермь,

Комсомольский пр., 29, e-mail: vmm@pstu.ru).

About the authors

Sukhodoeva Alla Alekseevna (Perm, Russia) – Ph.D. of Technical Sciences, Associate Professor, Department of Computational Mathematics and Mechanics, Perm National Research Polytechnic University (29, Komsomolsky av., Perm, 614990, Russia, e-mail: sukhodoeva @ya.ru).

Tikhomirova Kseniya Alekseevna (Perm, Russia) – student, Department of Dynamic and Strength of Mechanism, Perm National Research Polytechnic University (29, Komsomolsky av., Perm, 614990, Russia, e-mail: vmm@pstu.ru).

193

УДК 539.376

К.А. Тихомирова, Н.А. Труфанов

Пермский национальный исследовательский политехнический университет, Пермь, Россия

ЧИСЛЕННЫЙ АНАЛИЗ ПОЛЕЙ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ В НЕОДНОРОДНОМ СТЕКЛУЮЩЕМСЯ ЦИЛИНДРЕ

Представлено решение задачи формирования поля остаточных напряжений в длинном осесимметричном цилиндре из неоднородного по радиусу материала в процессе его охлаждения, сопровождающегося релаксационным переходом из размягченного состояния в застеклованное. Рассмотрен вариант новых физических соотношений, использующих представление о стеклующемся материале как смеси размягченного и застеклованного материалов. Численное решение ведется методом конечных разностей. Исследована практическая сходимость разностного решения. Дан численный прогноз распределения остаточных напряжений при изготовлении стержня из неоднородно легированного кварцевого стекла.

Ключевые слова: релаксационный переход, функция стеклования, остаточные напряжения, термомеханическая кривая, метод конечных разностей.

K.A. Tikhomirova, N.A. Trufanov

Perm National Research Polytechnic University, Perm, Russia

NUMERICAL ANALYSIS OF THE FIELDS OF RESIDUAL STRESSES IN NON-UNIFORM VITRIFICATED CYLINDER

The problem of forming of residual stresses in long axicymmetric cylinder with non-uniform radian distribution of doping degrees caused by cooling with relaxation transition is studied. A new version of physical relations, which is based on representation of vitrificated materials as a mixture of soft and solid parts, is considered. A numerical analysis of the problem is executed with the finite difference method. A practical convergence of finite difference solution has been analyzed. A numerical forecast of distribution of technological residual stresses in non-uniformly doped silica cylinder is done.

Keywords: relaxation transition, the function of vitrification, residual stresses, thermomechanical curve, finite difference method.

Введение

В заготовках кварцевых оптических световодов, поддерживающих поляризацию светового сигнала, используются так называемые силовые элементы, представляющие собой кварцевый цилиндрический стержень, содержащий легирующие добавки оксида бора с переменной

194

по радиусу концентрацией [1]. Введение легирующих элементов в основной материал стержня вызывает неоднородность термомеханических характеристик, что приводит при охлаждении стержня после изготовления к появлению остаточных напряжений [2], уровень которых достаточно высок и может приводить к растрескиванию заготовки.

Концентрация легирующих добавок в таком стержне не превышает 10 %, однако она существенно влияет на термомеханические свойства кварца, такие как коэффициент линейного температурного расширения (ЛКТР) и зависимость вязкости от температуры (в частности, на температуру стеклования и размягчения) [3].

1. Постановка задачи

Рассматривается задача о формировании поля остаточных напряжений в длинном цилиндрическом стержне из неоднородного по радиусу материала при его охлаждении в диапазоне температур, включающем температурный интервал стеклования материала.

Кварцевый цилиндр радиусом R = 5·10–3 м имеет неоднородное легированное ядро радиусом R0 = 3·10–3 м, внутри которого термомеханические характеристики материала изменяются по радиусу (рис. 1).

Рис. 1. Зависимость ЛКТР материала в застеклованном состоянии (--) и температуры стеклования (–) от радиуса

Коэффициент линейного температурного расширения (ЛКТР) α для материала в размягченном состоянии в 4 раза больше, чем в застеклованном:

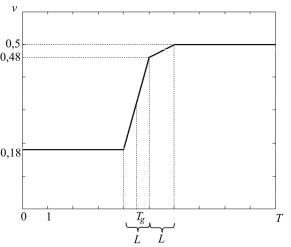
Из экспериментальных данных известно, что величины упругих характеристик кварца слабо зависят от температуры [4]. Поэтому было принято допущение, что модуль упругости Е материала не зависит от температуры. Коэффициент Пуассона ν для застеклованного состояния материала также принят не зависящим от температуры, а для размягченного состояния – изменяющимся согласно закону, представленному на рис. 2.

Установлено также, что значения упругих характеристик кварца мало зависят от концентрации легирующих элементов [4]. Следовательно, для застеклованного материала величины упругих характеристик являются константами радиуса и температуры. Но поскольку коэффициент Пуассона для размягченного материала зависит от температуры стеклования Tg, переменной по радиусу (см. рис. 1), то упругие характеристики размягченного состояния материала являются функциями радиуса и температуры.

Рис. 2. Зависимость коэффициента Пуассона от температуры

Цилиндр охлаждается от начальной температуры Тн = 1800 °С до комнатной 20 °С. Из решения соответствующей задачи теплопроводности [2] было получено, что в процессе охлаждения разница температур внутри стержня и на поверхности достаточно мала, поэтому будем считать температуру постоянной по сечению стержня.

Задача является осесимметричной, длина цилиндра на порядок больше его диаметра. В процессе изготовления стержня реализуются

196

состояния, близкие к обобщенному плоско-деформированному состоянию (εz = ε0z = const) и к состоянию плоской деформации (εz = 0). За-

кономерности формирования полей остаточных напряжений в условиях обобщенной плоской деформации рассмотрены в [2]. В данной работе исследуется состояние стержня в условиях плоской деформации.

Математическая постановка задачи в полярной системе координат (r, φ) с учетом малости деформаций и несущественности вклада массовых сил включает следующие соотношения:

– уравнение равновесия:

– геометрические соотношения:

Начальные условия соответствуют естественному начальному ненапряженному и недеформированному состоянию стержня:

где t – время, u(t, r) – радиальные перемещения, σr, σφ, εr, εφ – радиальные и окружные напряжения и деформации соответственно.

В качестве физических соотношений приняты уравнения, предложенные в работах [5, 6]. Они построены на предположении, что в каждый момент времени любой малый объем материала представляет собой смесь застекловавшейся и размягченной частей. Относительная доля застеклованного материала определяется функцией стеклования N(T), которая принимает значения от 0 до 1. Доля размягченной части составляет соответственно (1–N(T)). Застеклованный материал является упругим, а размягченный – вязкой средой. Исходя из этих предположений смесевые соотношения для шаровых и девиаторных частей тензоров напряжений и деформаций имеют вид:

197

где В – объемный модуль материала в застеклованном состоянии; Вж – в размягченном; G – модуль сдвига; η – вязкость; Sij и eij – компоненты девиаторов тензоров напряжений и деформаций соответственно. За Θ% обозначена разница общего и температурного объемного расширения:

Θ% = Θ−ΘT .

Вязкость η задается кусочно-непрерывной функцией, построенной на основе соотношений Аррениуса:

где K1, K2 – характеристики материала; L – длина интервала стеклования. Считая закон изменения температуры известным, от температурных зависимостей можно перейти к временным. В компонентной записи со-

отношения (6) для нормальных напряжений можно представить в виде

Индекс i здесь поочередно принимает значения r, φ, z. Поскольку принята гипотеза о плоском деформированном состоянии, то осевая деформация εz = 0. Тогда общее объемное расширение материала

Θ = εr + εφ.

Для одноосного случая смесевые соотношения (6) имеют следующий вид:

198

где ε% – разница общей и температурной деформации, ε% = ε−εT . Функцию N(T) удобно представить в виде распределения Лапласа:

Параметр Tg, входящий в данное распределение, является характеристикой материала и соответствует средней температуре интервала стеклования; γL – показатель длины интервала стеклования. Значения данных параметров подбирались из аппроксимации решения одномерной тестовой задачи, построенного по соотношениям модели Максвелла для вязкоупругого тела:

Рассматривалась задача о стержне, защемленном с обоих концов. Стержень сначала охлаждается с постоянной скоростью от температуры, превышающей Tg, затем производятся его разгрузка и равномерный нагрев. На рис. 3 представлена термомеханическая кривая, построенная по соотношениям (10), и ее аппроксимация смесевыми соотношениями (8).

Рис. 3. Термомеханическая кривая защемленного кварцевого стержня

при скорости охлаждения и нагрева T& = 10 °С/мин: – – с использованием соотношений (10); -- – с использованием соотношений (8)

199

Как видно из рис. 3, в одноосном случае смесевые соотношения и соотношения модели Максвелла позволяют получить хорошее соответствие результатов.

2. Построение конечно-разностного аналога краевой задачи

Общий пошаговый конечно-элементный алгоритм решения краевых задач термомеханики стеклующихся тел изложен в [7]. Рассмотрим конечно-разностный метод решения поставленной задачи, реализацию которого будем вести в перемещениях. Подставим в уравнение равновесия (2) геометрические соотношения (3) и физические соотношения (7). Тогда уравнение равновесия в перемещениях будет иметь вид:

200