Краткий курс общей физики

новесия, независимо от их природы, называют квазиупругими. Коэффициент пропорциональности k m 02 называют коэффициентом квази-

упругой силы. Под действием квазиупругой силы типа (1.100) тело будетсовершатьгармоническиеколебанияпозакону(1.96).

Квазиупругая сила обусловливает наличие у тела потенциальной энергии:

1.3.2. Маятники

По второму закону Ньютона для маятника, отклоненного от положения равновесия, с учетом (1.104):

max mg Fупрx mg k(x ) kx.

51

стоящая из невесомой и нерастяжимой нити, на которой подвешено тело, масса которого сосредоточена в одной точке и которое может совершать колебания под действием силы тяжести.

Отклонение маятника от положения равновесия (при колебаниях вокруг горизонтальной оси z) будем характеризовать углом , образованным нитью с вертикалью. Возникающий при этом момент силы тяжести стремится вернуть систему в положение равновесия (его действие аналогично действию квазиупругой силы (1.100)): M z mg sin , где sin – плечо силы тяжести.

52

Применим основное уравнение динамики вращательного движения (1.72) для маятника, отклоненного от положения равновесия

шись рассмотрением малых колебаний, можно положить sin φ φ.

С учетом того, что d2 2 , приходим к дифференциальному урав- dt

нению колебаний математического маятника:

Получено уравнение типа (1.99) относительно угла поворота (углового смещения):

где 02 g .

Отсюда циклическая частота колебаний математического маятника

где φmax и определяются из начальных условий.

Физический маятник – твердое тело, способное под действием силы тяжести совершать колебания вокруг неподвижной оси, не проходящей через его центр масс (рис. 1.26, б).

Применим основное уравнение динамики вращательного движения (1.72) для маятника, отклоненного от положения равновесия:

Iz mgbsin ,

53

где Iz – момент инерции тела относительно горизонтальной оси z, проходящей через точку подвеса; b – расстояние от точки подвеса до центра масс; bsin – плечо силы тяжести.

Рассматривая только малые отклонения ( sin ), приходим к дифференциальному уравнению колебаний физического маятника:

Получено уравнение типа (1.109) относительно угла поворота (углового смещения), решением которого является функция (1.112). При этом циклическая частота колебаний физического маятника

будет иметь такой же период колебаний, как и данный физический маятник. Величину пр называют приведенной длиной физического

маятника. Таким образом, приведенная длина физического маятни-

ка пр – это длина такого математического маятника, период коле-

баний которого совпадает с периодом колебаний данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром масс, удаленная на расстояние приведенной длины от оси вращения, называется центром качания физического маятника (точка O′ на рис. 1.26, б).

По теореме Штейнера момент инерции маятника Iz может быть представлен в виде

54

где IzC – момент инерции тела относительно оси, проходящей через

центр масс и параллельной оси вращения z; b – расстояние между осями.

Подставив (1.110) в (1.109), получаем:

откуда следует, что пр > b, так что точка подвеса и центр качания лежат по разные стороны от центра масс.

1.3.3. Сложение колебаний

Сложение колебаний одинакового направления и одной частоты

На практике часто приходится иметь дело с таким движением, при котором тело участвует одновременно в двух или нескольких колебаниях. Например, если груз подвешен на пружине к потолку вагона, то груз совершает колебания относительно точки подвеса, которая, в свою очередь, колеблется на рессорах вагона. Таким образом, груз совершает движение, складывающееся из двух колеба-

вилам сложения векторов ре-

зультирующий вектор A . Проекция этого вектора на ось х равна сум-

мепроекций слагаемыхвекторов: х= х1 + х2.

Следовательно, вектор A представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью 0, что

55

и векторы A1 и A2 , так что результирующее движение будет гармоническимколебаниемсчастотой 0, амплитудойАиначальнойфазой :

Проанализируем выражение (1.121) для амплитуды:

1)если разность фаз обоих колебаний 2 1 = 0, то амплитуда результирующего колебания А = А1 + А2;

2)если 2 1 = , т.е. оба колебания находятся в противофа-

будут вращаться с различной угловой скоростью. В этом случае ре-

зультирующий вектор A пульсирует по величине и вращается с непостоянной скоростью. Результирующим движением в этом случае будет не гармоническое колебание, а некоторый сложный процесс.

Биения

Особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления имеют одинаковую амплитуду и мало отличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармонические колебания с пульсирующей амплитудой. Такие колебания называются биениями.

Поскольку частоты колебаний несколько отличны, всегда можно выбрать начало отсчета времени так, чтобы начальные фазы обоих колебаний были равны нулю. Если ω2 – ω1 = ∆ω и

при этом 0 .

56

Складывая эти выражения и применяя тригонометрическую формулу для суммы косинусов, получим:

множитель в формуле (1.123) изменяется гораздо медленнее, чем второй множитель. Вследствие условия 0 >> за то время, за ко-

торое множитель cos 0t совершает несколько полных колебаний, множитель, стоящий в скобках, почти не изменится.

зан на рис. 1.28, б. Амплитуда – величина положительная, поэтому выражение для результирующей амплитуды, очевидно, имеет вид

Выражение (1.124) является периодической функцией с частотой, в два раза превышающей частоту выражения, стоящего под знаком модуля, т.е. с частотой . Таким образом, частота пульсаций амплитуды – ее называют частотой биений – равна разности частот складываемых колебаний. Период биений Та = 2π/(∆ω).

Сложение взаимно перпендикулярных колебаний

Примером сложения колебаний различного направления является движение следа пучка электронов на экране электроннолучевой трубки (например, осциллографа) под действием на пучок двух взаимно перпендикулярных переменных электрических полей.

Рассмотрим результат сложения двух взаимно перпендикулярных гармонических колебаний одной частоты 0, происходящих вдоль координатных осей x и y. Если возбудить оба колебания, то

57

материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.

Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний можно записать следующим образом:

где разность фаз складываемых колебаний.

Выражение (1.125) представляет собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Исключив из этих уравнений параметр времениt, можнополучитьуравнение траекториивнеявном виде:

Из аналитической геометрии известно, что уравнение (1.126) есть уравнение эллипса, оси которого ориентированы относительно координатных осей x и y определенным образом.

Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд А и В и разности фаз .

Исследуем форму траектории в некоторых частных случаях: 1. = 0. В этом случае уравнение (1.126) принимает вид

откуда получается уравнение прямой (рис. 1.29, а):

Рис. 1.29

58

2. = . Уравнение (1.126) принимает вид

3. = /2. Уравнение (1.126) переходит в уравнение эллипса

(рис. 1.29, в):

приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд эллипс вырождается в окружность. Случаи / 2 и / 2 отличаются направлением движения по эллипсу или по окружности.

Из сказанного следует, что равномерное движение по окружности радиусом R с угловой скоростью 0 может быть представлено как сумма двух взаимно перпендикулярных колебаний:

Знак «+» в выражении для y соответствует движению против часовой стрелки, знак « » – движению по часовой стрелке.

В случае, когда частоты взаимно перпендикулярных колебаний отличаются на очень малую величину , их можно рассматривать как колебания одинаковой частоты, но с изменяющейся разностью фаз. Результирующее движение в этом случае происходит по медленно видоизменяющейся кривой, которая последовательно принимает форму, отвечающую всем значениям разности фаз от до + .

Если частоты взаимно перпендикулярных колебаний неодинаковы, то траектория результирующего движения может иметь вид довольно сложных кривых, называемых фигурами Лиссажу. На рис. 1.30 показана одна из простейших траекторий, получающаяся при отношении частот 1:2, разности фаз, равной /2 (а) и нулю (б). Уравнения колебаний имеют следующий вид:

59

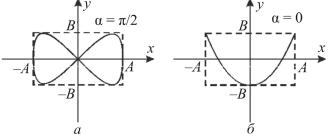
x Acos 0t,

y B cos(2 0t ).

За то время, пока вдоль оси x точка успевает переместиться из одного крайнего положения в другое, вдоль оси y, выйдя из нулевого положения, она успевает достигнуть одного крайнего положения, затем другого и вернуться в нулевое положение (см. рис. 1.30, а).

Рис. 1.30

Вслучае разности фаз, равной нулю, траектория вырождается

внезамкнутую кривую (см. рис. 1.30, б), по которой точка движется туда и обратно.

1.3.4. Затухающие колебания

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Затухающими называются колебания, происходящие вдиссипативнойколебательнойсистеме.

Уравнение затухающих колебаний

При небольших скоростях движения сила сопротивления среды пропорциональна скорости:

где r коэффициент сопротивления среды. Знак «минус» обусловлен тем, что сила и скорость имеют противоположные направления.

Уравнение движения (второй закон Ньютона) при наличии квазиупругих сил и сил сопротивления имеет вид:

max kx rvx .

60