
Краткий курс общей физики
..pdf
Средняя скорость перемещения vср – отношение перемещения к затраченному на него времени:
|
r |
|
vср |
t . |
(1.5) |
Скорость (мгновенная)
Вектор скорости v
(рис. 1.3).
Модуль скорости
v |
|
v |
|
lim |
|
r |
|
|
|
|
|
|
|||||
|
|
|||||||
|
|
|
|
|
||||
|
|
|
t |
|
||||
|
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|
v lim |
r |
dr . |
(1.6) |
t 0 |
t |
dt |
|
направлен по касательной к траектории
|
(t |
|
|
|
|
|
|
v |
|
|
|
|
|
1 |
) |
|
2 |
v |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
v |
|
( |
|
|
|
|
|
t+ |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
v |
|
|
|
|
) |
|
( |
|
|
|
|
|
|
t |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
) |
|
|
|
|
lim |
s |
ds |
. (1.7) |
Рис. 1.3 |
t 0 |
t |
dt |
|
|
Быстрота изменения скорости со временем характеризуется ускорением. Средним ускорением aср называют отношение изменения
вектора скорости ко времени:
aср v t , [a] = м/с2.
t , [a] = м/с2.
Ускорение (мгновенное)
a lim v dv d2r .
t 0 t dt dt2
Скорость и ускорение можно разложить на составляющие: v vxi vy j vz k , a axi ay j az k ,
(1.8)
(1.9)
где компоненты – это проекции на координатные оси этих векторов:
|
dx |
; |
|
|
|
|
dvx |
|
d2 x |
|
; |
|
|||
vx |
dt |
ax |
dt |
dt |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dy |
|
|
|
|
|
dvy |
|
d2 y |
|
|
||||
vy |
|
; |
ay |
|
|
|
|
|
2 |
|
; |
(1.10) |
|||
dt |
dt |
dt |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
vz |
dz |
; |
|
a |
|
|
dv |
z |
|
d2 z |
. |
|
|||
|
|
z |
|
|
2 |
|
|||||||||
|
dt |
|
|
|
dt |
|
dt |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
11
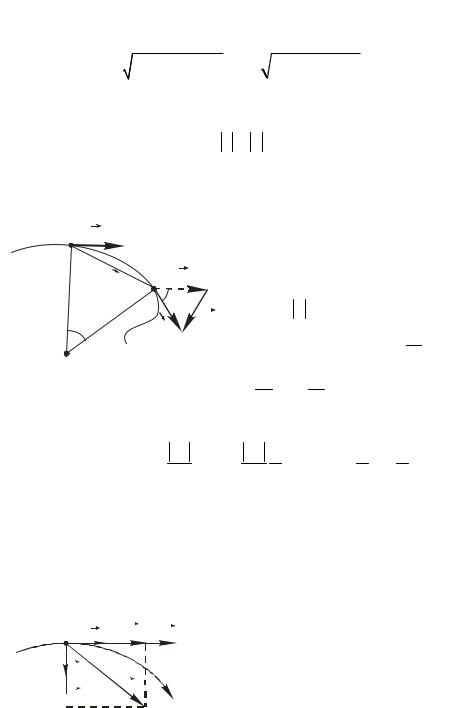
Модули скорости и ускорения в этом случае находятся по фор- |
||||||||||||||||||||
мулам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
vx |
2 vy |
2 vz |
2 , a |
ax |
2 |
ay |
2 az |
2 . |
|
|
|
|
(1.11) |
|||||
При криволинейном движении удобно ввести естественные |
||||||||||||||||||||
оси, направления которых задаются единичными векторами каса- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тельной и нормали n : |
n , |
n 1. |
|
|
|
|
|
|
|
|
|
|
||||||||
Вектор |
|
направлен по касательной к траектории (рис. 1.4) и |
||||||||||||||||||
задает направление вектора скорости, |
вектор n направлен по нор- |
|||||||||||||||||||
мали к траектории (к центру кривизны). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
(t) |
|
|
|
|
|
|
Вектор |
|
скорости |
|
можно |
||||||||
|
|
|
|
|
|
|
|
представить в виде |
|
|
|
|
|
|||||||
|
|
s |
|
(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
v v , |
|
|
|
|
(1.12) |
|||||||
R |
|
r| |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
R |
|
|
|
|
где v v . Тогда по определению |
||||||||||||||
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
t |
|
|
|
|
|
|
|
|
|
dv |
|
d |
|
||||||
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
ускорение |
|
a |
|
|
|
|
v |
|||||||
|
|
|
|
|
t |
|
|
dt |
dt |
|||||||||||
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
dv |
|
d |
|
|
|
|
|
|||||
|
Рис. 1.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поскольку |
|
|
|
|
|
dt |
v dt . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
n lim |
1 n |
|
|
|
|
1 n |
v n, |
||||||||
d lim |
|
lim |
r |
lim |
s |
|
||||||||||||||
dt |
t 0 |
t |
t 0 |
t |
t 0 |
t R |
|
t 0 |
t R |
|
|
R |
|
|
||||||
где R – радиус кривизны траектории в данной точке, то |
|
|
|
|
||||||||||||||||
|
|
dv |
v2 |
|
|
|
|
(1.13) |
||
a |
dt |
|
R |
n |
a ann |
a an . |
||||
|
|
|
|
|
|
|
|
|
||
Таким образом, ляющие (рис. 1.5).
O a
n
 an a
an a
Рис. 1.5
ускорение можно разложить на две состав-
Касательным (тангенциальным)
vускорением a называется составляющая ускорения, обусловленная изме-
нением модуля вектора скорости:
|
|
|
|
(1.14) |
|
|
|
a a , |
|
где |
a |
dv |
. |
|
|
|
|||
|
|
dt |
|
|
12

Нормальным (центростремительным) ускорением an называ-
ется составляющая ускорения, обусловленная изменением направления движения (т.е. вектора ):
a |
a n |
, |
(1.15) |
n |
n |
|
|
где an v2 .
R
Модуль ускорения
a a |
2 a 2 . |
(1.16) |
|
n |
|
Примеры:
1. При равномерном прямолинейном движении точки вдоль оси x
vx const a 0, |
a 0. |
||
R |
an 0 |
|
|
|
|
||
Закон равномерного движения:
xx0 vxt.
2.При равнопеременном прямолинейном движении
a x const, |
|
|
ax a x const. |
R an |
|
||
0 |
|
|
Закон изменения скорости: |
|
|
|
|
|
|
|
vx v0 x axt. |
|
|
|
(1.17) |
|||
Закон движения: |
|
|
|
|
|
|
|
x x |
v |
|
t |
a |
t2 |
. |
(1.18) |
0x |
x |
|
|||||
|
|
||||||
0 |
|
|
2 |
|
|
||
|
|
|
|
|
|
||
Исключив параметр времени t из уравнений (1.17), (1.18), можно прийти к полезному соотношению:
x x |
|
v 2 |
v |
2 |
. |
(1.19) |
x |
|
0 x |
||||
|
|
|
||||
0 |
|
2 ax |
|
|
|
|
|
|
|
|
|
||
3. При равномерном движении по окружности радиусом R
13

v const |
a 0, |
|
|
||
|
|
|
|
|
a an const . |
an |
v2 |
const |
|
||
R |
|
|
|||
|
|
|
|
|
|
Закон движения:
0 v (t t0 ),
где – криволинейная координата, направленная вдоль траектории
(см. рис. 1.5).
4. При равнопеременном движении по окружности радиусом R
a const, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
a |
a |
2 |
a |
|
2 |
. |
an |
v |
2 |
|
|
|
n |
|
|||||
|
const |
|
|
|
|
|
|
|
||||
R |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
Закон изменения скорости: v v0 a (t t0 ). Закон движения: 0 v0 (t t0 ) 12 a (t t0 )2 .
Примечание. При поступательном движении абсолютно твердого тела скорости и ускорения всех точек равны по величине и направлению, а траектории всех точек одинаковы, поэтому кинематику поступательно движущегося твердого тела рассматривают как кинематику точки.
1.1.2. Кинематика вращательного движения
Вращательное движение абсолютно твердого тела – движение, при котором все точки тела в данный момент движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Пусть твердое тело, вращаясь вокруг некоторой оси OO , совершило за время dt бесконечно малый поворот. Соответ-
ствующий угол поворота будем характеризовать вектором dφ, модуль которого равен углу поворота dφ, а направление совпадает с осью OO , причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора dφ
(рис. 1.6). Единица измерения угла поворота – радиан, [ ] = рад. Положение некоторой точки A зададим радиусом-вектором r ,
проведенным из некоторой точки O на оси вращения. Тогда модуль линейного перемещения dr точки A связан с углом поворота dφ
14

соотношением |
|
dr |
|
r sin θ dφ, |
где θ – |
|
|||
|
|
|
|||||||
угол между векторами r и dφ. В век- |
|
||||||||
торном виде |
|
|
|
|
|||||
|
|
|
dr dφ r. |
(1.20) |
|
||||
Отметим, что это равенство спра- |
|
||||||||
ведливо лишь для бесконечно малого |
|
||||||||
угла поворота dφ. Другими словами, |
|
||||||||
только бесконечно малые повороты |
|
||||||||
можно рассматривать как векторы. Для |
|
||||||||
конечного поворота на угол линей- |
|
||||||||
ноеперемещениеточкиA (см. рис. 1.6) |
Рис. 1.6 |
||||||||
|
r |
|
|
|
|
|
|
|
|
|
|
2r sin θsin φ/ 2 . |
|
|
|||||
|
|
|
|
||||||
Отсюда сразу видно, что перемещение r нельзя представить |
|||||||||
|
|
|
|
|
|
|
|
|
и r . Это возможно лишь |
как векторное произведение векторов dφ |
|||||||||
в случае бесконечно малого поворота dφ |
, в пределах которого ра- |
||||||||
диус-вектор r можно считать неизменным.
Введенный вектор dφ удовлетворяет свойству коммутативности
векторов. Чтобы убедиться в этом, представим, что твердое тело со- |
|||||||
вершает два элементарных поворота |
|
|
|
||||
dφ1 |
и dφ2 вокруг разных осей, |
||||||
проходящих через неподвижную точку O. В этом случае результи- |
|||||||
рующее перемещение dr |
произвольной точки A тела, радиус-вектор |
||||||
которойотносительноточкиO равен r , можнопредставитьтак: |
|||||||
dr dr dr |
dφ |
r |
dφ |
r dφ r , |
|||
1 |
2 |
1 |
|
|
2 |
|
|
где |
dφ dφ1 dφ |
|
|
|
|||
|
2 . |
|
(1.21) |
||||
Таким образом, два данных поворота, dφ1 и dφ |
2 , эквивалентны |
||||||
одному повороту на угол dφ dφ1 dφ2 |
вокруг оси, совпадающей |
||||||
с вектором dφ и проходящей через точку O.
В отличие от таких величин, как r , v , a , векторы типа dφ,
направление которых связывают с направлением вращения, назы-
вают псевдовекторами или аксиальными векторами.
15

Угловая скорость
|
|
|
|
dφ |
|
|
|
ω |
|
, |
(1.22) |
dt |
где dt – промежуток времени, за который тело совершает поворот dφ.
Как следует из определения, вектор ω совпадает по направлению с вектором dφ и представляет собой псевдовектор, направленный вдоль оси вращения. Единица измерения угловой скорости –
радиан в секунду, [ ] = рад/с.
Рассмотрим движение твердого тела, вращающегося с угловой
скоростью ω1 вокруг оси OA (рис. 1.7), которая, в свою очередь, вращается вокруг оси OB с угловой скоростью ω2 . За промежуток времени dt тело совершит поворот dφ1 вокруг оси OA и одновременно поворот dφ2 вокруг оси OB.
|
|
|
Согласно (1.21) суммарный |
||||
|
|
|
поворот dφ dφ1 |
dφ2 . Поделив |
|||
|
|
|
обе части этого равенства на dt , |
||||
|
|
|
получим закон сложения угло- |
||||
|
|
|
выхскоростей: |
|
|
|
|
|
|
|
|
|
|
(1.23) |
|
|
|
|
|
ω ω1 |
ω2 . |
||
|
|
|
Изменение вектора |
|
со |
||
|
|
|
ω |
||||
|
|
|
временем характеризуют векто- |
||||
Рис. 1.7 |
|
|
ром углового ускорения, который |
||||
|
|
такжеявляетсяпсевдовектором: |
|||||
|
|
dω |
2 |
|
|
|
|
ε |
|
, [ ] = рад/с |
. |
|
(1.24) |
||
dt |
|
||||||
Вращение вокруг неподвижной оси – частный случай вращатель-
ного движения. В этом случае траекториями всех точек являются окружности, центрыкоторыхлежатнаоднойнеподвижнойпрямой.
Положение тела в пространстве определяется углом поворота.
Закон вращения: |
|
φ φ(t) . |
(1.25) |
16

Положительное направление оси свяжем с положительным направлением угловой координаты (угла поворота ) правилом правого винта (рис. 1.8).
В случае неподвижной оси угловая скорость характеризуется алгебраической величиной:
ωz dφ . |
(1.26) |
|
|
||
|
dt |
|
|
|
|
Аналогично угловое ускорение |
Рис. 1.8 |
|
|||
εz |
dωz |
. |
(1.27) |
|
|
|
|
|
|||
|
dt |
|
|
|
|
Знаквеличин ωz и εz |
определяетсянаправлениемсоответствующе- |
||||
|
|
|
|
|
совпадает |
го вектора. Например, если ωz 0 , то направление вектора ω |
|||||
с положительным направлением оси Z, если же ωz 0, то направление вектора ω противоположно(такжеидляугловогоускорения).
1.1.3. Связь между линейными и угловыми величинами
Поделив соотношение (1.20) на соответствующий промежуток
времени dt с учетом (1.6) и (1.22), получаем связь между линейной |
|
и угловой скоростями: |
|
|
(1.28) |
v ω r. |
|
Таким образом, скорость v любой точки A твердого тела, вра- |
|
щающегося вокруг некоторой оси с угловой скоростью ω, равна век- |
|||||||||
торномупроизведениюугловойскорости ω на радиус-вектор r |
точки |
||||||||
A относительнопроизвольной точкиO осивращения(рис. 1.9). |
|
||||||||
Модуль |
|
вектора |
|
скорости |
|
|
|||
v ωr sin , |
или |
|
|
|
|
|
|
||
|
|
v ωR, |
|
|
(1.29) |
|
|
||
где R – радиус кривизны траектории, по |
|
|
|||||||
которой движется точка A. |
|
|
|
||||||
Продифференцировав соотношение |
|
|
|||||||
(1.28) по времени, найдем ускорение a |
|
|
|||||||
|
|
dω |
|
|
dr |
|
|
|
|
точки A: a |
|
dt |
r |
ω dt |
, или |
|
|
||
|
|
|
|
|
|
|
(1.30) |
|
|
a |
ε r |
ω ω r . |
Рис. 1.9 |
|
|||||
|
|
|
|
|
|
|
|
|
|
17

В общем случае нахождение скорости и ускорения точек тела является непростой задачей, уже хотя бы потому, что при повороте оси вращения точка O не является неподвижной, хотя скорость точки тела в ней равна нулю (по определению). Сложность, в частно-
сти, состоит в определении координат радиуса-вектора r .
В случае неподвижной оси ε|| ω, поэтому первое слагаемое со-
отношения (1.30) будет представлять собой тангенциальное ускорение:
a ε r , |
(1.31) |
а второе слагаемое – нормальное ускорение:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.32) |
||
|
|
|
|
|
|
|
an ω |
ω r . |
|
|
|
|
|
|
|
|
|||||
Модули этих ускорений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
a εR; |
|
an ω2 R. |
|
|
|
|
|
|
|
|
(1.33) |
|||
Тогда полное ускорение |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
a a |
2 a |
2 R ε2 ω4 |
. |
|
|
|
|
|
(1.34) |
|||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||
В кинематике поступательного и вращательного движений су- |
|||||||||||||||||||||
ществуют следующие аналогии: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
Поступательное движение |
|
|
|
Вращательное движение |
|||||||||||||||||
|
|
|
|
|
|
|
Определения |
|
|
|
|
|
|
|
|
|
|||||
Координата |
|
|
x, м |
|
|
|
Угол поворота |
|
|
, рад |
|||||||||||
Скорость |
vx |
dx |
, |
м/с |
|
Угловая скорость |
|
z |
|
dφ |
, рад/с |
||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
||
Ускорение |
ax dvx |
, |
м/с2 |
|
|
Угловое ускоре- |
z d z |
, рад/с2 |
|||||||||||||
|
|
|
dt |
|
|
|
|
|
|
|
ние |
|
|
|
|
|
dt |
|
|||
|
Законы равнопеременного движения |
|
|
|
|
|
|
||||||||||||||
ax const |
|
|
|
|
|
|
|
|
|
εz const |
|
|
|
|
|
||||||
vx v0 x axt |
|
|
|
|
|
|
|
ωz ω0 z εzt |
|
|
|
|
|||||||||
x x v |
t |
a |
t2 |
|
|
|
|
|
φ φ |
|
φ |
|
t |
ε |
|
|
t2 |
|
|||
|
x |
|
|
|
|
|
|
|
0 |
0 z |
|
z |
|
|
|||||||
0 |
0x |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
18

Примеры решения задач
№ 1. Уравнение движения точки по прямой имеет вид:
х = А + B t + C t3 (А = 4 м, В = 2 м/с, С = 0,2 м/с3). Найдите сред-
нюю скорость за промежуток времени от 2 до 5 с.
Ре ш е н и е.
vx x x2 x1 (4 2 5 0,2 53 ) (4 2 2 0,2 23 )
t t2 t1 5 2
|
39 9,6 9,8 м/с. |
||
|
3 |
|
|
№ 2. График зависимости проекции |
|
|
|
vx , |
|||
скорости тела vx |
на ось х от времени t |
|
|
|
|||
приведен на рисунке. Чему равна проек- |
|||
ция ускорения тела на эту ось? |
|||
Р е ш е н и е. Мгновенное ускорение |
|||
a dv , его проекция на ось х ax dvx . |
|||
dt |
dt |
||
Если скорость меняется по линейному закону, то проекцию ус- |
|||
корения можно искать по формуле |
|||
a |
x |
|
vx |
|
vx2 vx1 |
. |
|
|
|
|||
|
|
|
|
|||||||||
|
|
t |
|
t |
2 |
t |
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Взяв интервал времени от 0 |
до 4 |
с, получим: |
ax |
4 4 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
4 0 |
|
2м/с2.
№3. Автомобиль начинает движение с ускорением 1 м/с2. Проезжая мимо наблюдателя, он имел скорость 10,5 м/с. На каком расстоянии от наблюдателя он находился секунду назад?
Р е ш е н и е. Кинематическое уравнение равнопеременного
движения вдоль оси х (а = const) имеет вид: x x |
v |
|
t |
at2 |
, где |
0 |
|
||||
0 |
|
|
2 |
|
|
|
|
|
|
|
v0 – начальная скорость, t – время. Скорость точки при равнопеременном движении v = v0 + at.
Если автомобиль начинает движение, то v0 = 0, и v = at. Найдем время движения до наблюдателя:
t1 av 10,51 10,5 c; t2 = 10,5–1 = 9,5 с.
19

Примем начальное положение автомобиля за начало отсчета |
||||||||||
(х0 = 0). Тогда: |
x |
at2 |
|
1 10,52 |
55,125 м, |
x |
|
at2 |
1 9,52 |
|
1 |
|
2 |
|
|||||||
|
1 |
2 |
|
2 |
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
||||
45,125 м. |
|
|
|
|
|
|
|
|
|
|
Получим: х1 – х2 = 55,125 – 45,125 = 10 м.
№ 4. Тело падает вертикально с высоты Н = 19,6 м с нулевой начальной скоростью. За какое время тело пройдет первый и последний метры своего пути?
Д а н о: Н = 19,6 м, v0 = 0, |
h1 = 1 м, |
|
h2 = H – |
|||
– h = 1 м, g = 9,8 м/с2. |
|
|
|
|
|
|
Р е ш е н и е. Из формулы |
h |
g t2 |
найдем |
|||
|
1 |
|||||
|
|
|||||
|
|
|
1 |
2 |
|
|
время прохождения первого метра: |
|
|
||||
|
|
|
||||
t |
2 h1 |
2 1 0,452 с. |
|
|
||
1 |
g |
9,8 |
|
|
|
|
|
|
|
|
|
||
Время прохождения последнего метра найдем как разность времен прохождения путей H (время падения tпад) и h (время t0):
tпад |
2 H |
|
2 19,6 |
2 |
с, t0 |
2 h |
|
2 18,6 |
1,948 с; |
|
g |
|
9,8 |
|
|
g |
|
9,8 |
|
t2 = tпад – t0 = 2 – 1,948 = 0,052 с.
№ 5. Линейная скорость точек на ободе вращающегося диска равна 3 м/с. Точки, расположенные на 0,1 м ближе к оси вращения, имеют линейную скорость 2 м/с. Каковы угловая скорость и частота вращения диска?
Д а н о: v1 = 3 м/с, v2 = 2 м/с, R = R1 – R2 = 0,1 м.
Р е ш е н и е. Угловая скорость всех точек диска одинакова
и связана |
с |
линейной |
формулой ω |
v |
. Тогда |
ω |
v1 |
|
v2 |
или |
|||||||||
|
R |
R |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
||
|
v1 |
|
v2 |
|
|
. Подставив числа, получаем уравнение с одним неиз- |
|||||||||||||
|
|
R R |
|||||||||||||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вестным |
|
3 |
|
|
|
2 |
|
, |
откуда радиус диска R1 = 0,3 м. Тогда угло- |
||||||||||
|
R |
R |
|
0,1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
20
