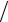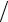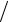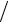и сделать оценку по модулю:
αmax 
 δθmax ≤ δf j + ∑ αk
δθmax ≤ δf j + ∑ αk 
 δθk .
δθk .
k≠max
Выбирается узел, в котором δθ достигает наибольшего значения. Одновременно усиливается последнее неравенство с помощью замены в правой час-
ти всех величин δθk на 
 δθ
δθ
 , а δf j – на
, а δf j – на 
 δf
δf 
 :
:
αmax 

 δθ
δθ
 ≤
≤ 
 δf
δf 
 +
+ 
 δθ
δθ
 ∑ αk .
∑ αk .
k ≠max
Полученное выражение преобразуется к виду
|
|
αmax |
|
− |
∑ |
|
αk |
|
|
|
|
|
|
|
|
|
≤ |
|
δf |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δθ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k ≠max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда, с учетом (10.24), получается
|
|
|
|
|
|
|
, |
ω δθ |
τ ≤ |
αmax − ∑ αk |
δθ ≤ δf |
|
|
|
|
k≠max |
|
|
|
|
δθ ≤ τ δf |
ω = στ δf , σ =1 ω, |
|
|
|
|
|
|
|
|
|
|
|
что совпадает с определением устойчивости разностной схемы по правой части. Что и требовалось доказать.
Условия рассмотренной теоремы формулируют лишь достаточные условия устойчивости. Иначе говоря, невыполнение условий (10.23)–(10.24) не означает неустойчивости разностной схемы.
Пример 10.2. Проверить условия устойчивости для неявной разностной схемы (10.18) задачи теплопроводности
θj−1 (−η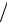 h2 )+ θj (1 τ+ 2η h2 )+θj+1 (−η
h2 )+ θj (1 τ+ 2η h2 )+θj+1 (−η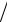 h2 )= θj
h2 )= θj 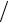 τ.
τ.
Для коэффициентов уравнения используются введенные обозначения
αmax =1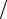 τ + 2η
τ + 2η h2 , α j−1 = −η
h2 , α j−1 = −η h2 , α j+1 = −η
h2 , α j+1 = −η h2 , βj =1
h2 , βj =1 τ.
τ.
Условие устойчивости по начальным данным (10.23) принимает вид неравенства
1 τ + 2η
τ + 2η h2 ≥ η
h2 ≥ η h2 + η
h2 + η h2 +1
h2 +1 τ,
τ,

выполняющегося для любых значений шагов τ и h. Следовательно, рассмотренная разностная схема безусловно устойчива. Условие устойчивости по правой части определяется выражением
1 τ + 2η
τ + 2η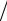 h2 − η
h2 − η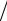 h2 − η
h2 − η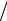 h2 ≥1 τ ≥ ω τ,
h2 ≥1 τ ≥ ω τ,
которое также выполняется для всех значений шагов τ и h (например, для 0 < ω<1). Общий вывод: рассмотренная неявная разностная схема безусловно устойчива как по начальным данным, так и по правой части.
Пример 10.3. Проверить условия устойчивости для явной разностной схемы (10.16) задачи теплопроводности
(θj −θj ) τ = η(θj+1 − 2θj + θj−1 )
τ = η(θj+1 − 2θj + θj−1 )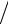 h2 .
h2 .
Разностное уравнение преобразуется к подходящему для анализа виду
θj τ = θj−1η h2 + θj (1 τ − 2η h2 )+ θj+1η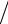 h2 .
h2 .
Очевидно, что в этом случае отличны от нуля коэффициенты
αmax =1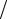 τ, βj+1 = η
τ, βj+1 = η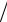 h2 , βj =1
h2 , βj =1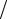 τ − 2η
τ − 2η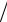 h2 , βj−1 = η
h2 , βj−1 = η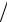 h2 .
h2 .
Условие устойчивости по начальным данным (10.23) принимает вид неравенства
1 τ ≥ η h2 + η h2 + 1 τ − 2η h2 ,
1 τ − 2η h2 ≤1 τ − 2η h2 ,
раскрывая которое,
2η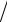 h2 −1 τ ≤1 τ − 2η
h2 −1 τ ≤1 τ − 2η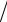 h2 ≤1
h2 ≤1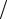 τ − 2η
τ − 2η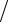 h2,
h2,
можно получить условие устойчивости по начальным данным,
Это означает, что рассматриваемая схема является условно устойчивой. Условие устойчивости по правой части
1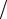 τ ≥ ω
τ ≥ ω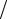 τ
τ
выполняется для всех значений 0 < ω < 1.
Общий вывод: явная разностная схема является условно устойчивой при выполнении условия (10.26), ограничивающего шаг интегрирования τ.

Метод Неймана1
Рассматривается разностная схема (10.16)
(θj −θj )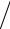 τ = η(θj+1 − 2θj + θj−1 )
τ = η(θj+1 − 2θj + θj−1 )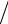 h2.
h2.
Если внести возмущение δθ в решение θ на каком-либо временном слое,
~ |
|
~ |
|
|
|
θ = θ + δθ, решение на следующем слое θ = θ+ δθ будет удовлетворять разно- |
стному уравнению |
~ ~ |
~ |
~ |
~ |
2 |
|
|
|
|
|
|
|
|
θ j − θj τ = η(θj+1 − 2θj + θj−1 ) |
h . |
|
|
|
|
|
|
Вычитание из этого соотношения предыдущего приводит к уравнению от- |
носительно погрешностей |
|
|
|
|
(δθ |
j − δθj ) τ = η(δθj+1 − 2δθj + δθj−1 ) h2 , |
которое удобно переписать в виде
δθj = δθj−1τη h2 + δθj (1−2τη h2 )+ δθj+1τη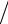 h2 .
h2 .
Погрешность δθ решения разлагается в ряд
|
|
|
|
|
|
|
n−1 |
|
|
|
|
|
|
|
δθ(x)= ∑ak eikx , |
(10.27) |
|
|
|
|
|
|
|
k=0 |
|
где eikx , k = |
|
|
|
|
– полная ортогональная система функций на равномерной |
0,n −1 |
сетке Ωn = {xk |
|
xk |
= kh, k = |
|
}; i = |
|
– |
мнимая единица. Произвольная k-я |
|
0,n |
−1 |
гармоника этого разложения
δθ(k )(x) = ak eikx
подставляется в разностное уравнение:
δθ(jk ) = ak eikx j−1 τη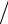 h2 + (1 − 2τη
h2 + (1 − 2τη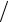 h2 )ak eikx j + ak eikxj +1 τη
h2 )ak eikx j + ak eikxj +1 τη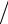 h2 = = ak eikx j [1 + (e−ikh − 2 + eikh )τη
h2 = = ak eikx j [1 + (e−ikh − 2 + eikh )τη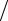 h2 ]= ρk ak eikx j = ρk δθ(jk ) .
h2 ]= ρk ak eikx j = ρk δθ(jk ) .
1 Джон Нейман фон [28.12.1903 – 8.2.1957] – американский математик. В 1926 году окончил Будапештский университет. В 1927–1929 годах преподавал в Берлинском университете, 1930–1933 – в Принстонском университете. С 1933 года – профессор Принстонского института перспективных исследований. С 1940 года работал консультантом армейских и морских учреждений; принимал участие в работах по созданию первой атомной бомбы. С 1954 года был членом комиссии по атомной энергии. Внес большой вклад в создание первых ЭВМ и разработку методов их применения.
Здесь ρk = [1 + (e−ikh − 2 + eikh )τη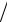 h2 ] – коэффициент роста
h2 ] – коэффициент роста
при переходе на следующий временной слой.
Для m временных слоев получается соотношение
(δθmj )(k ) = (ρk )m (δθ0j )(k ).
Учитывая формулу Эйлера1, выражение для коэффициента роста произвольной гармоники можно преобразовать к виду
ρk =1 + τη[cos(kh) − isin(kh)− 2 + cos(kh)+ isin(kh)] h2 |
= |
=1+ 2τη[cos(kh)−1] h2 =1− 4τηsin2 (kh 2) h2. |
(10.29) |
|
В общем случае разностное уравнение |
|
B(θ |
j − θj ) τ + Aθj = ϕj |
(10.30) |
относительно погрешностей δθj (при отсутствии возмущения правой части) записывается в виде
Bδθj = (B − τA)δθj .
Подстановка в него выражений для δθj приводит к уравнению относительно коэффициента роста произвольной гармоники
ρk Beikxj = (B − τA)eikxj .
Теорема 10.4 (признак устойчивости Неймана). Разностная схема с постоянными коэффициентами устойчива по начальным данным, если для всех k выполняется неравенство
|
ρk |
|
≤1 + Cτ, C = const ≥ 0. |
(10.31) |
|
|
Доказательство. Возмущение начальных данных разлагается в ряд:
δθ(t0 , x j )= ∑n−1 ak eikxj. k =0
Подстановка этого разложения в разностную схему (10.30) благодаря линейности последней приводит к выражению
δθ(tm , x j )= ∑n−1 (ρk )m ak eikx j . k=0
На разностной сетке Ω в силу ортогональности гармоник
1 Формула Эйлера: cos x + i sin x = eix .

|
|
|
|
|
|
n−1 |
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
|
)2m |
|
|
|
|
|
|
|
|
|
δθ(tm ) |
|
|
|
l2 |
= n∑ |
|
ak |
|
2 |
|
ρk |
|
2m ≤ n(max |
|
ρk |
|
)2m ∑ |
|
ak |
|
2 = (max |
|
ρk |
|
|
|
|
δθ(t0 ) |
|
|
|
l2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
k=0 |
|
|
|
|
|
k |
|
|
|
k=0 |
|
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В соответствии с условием1 (10.31),

 δθ(tm )
δθ(tm )
 l22 = (1 + Cτ)2m
l22 = (1 + Cτ)2m 
 δθ(t0 )
δθ(t0 )
 l22 ,
l22 ,

 δθ(tm )
δθ(tm )
 l2 = (1 + Cτ)m
l2 = (1 + Cτ)m 
 δθ(t0 )
δθ(t0 )
 l2 .
l2 .
Последнее выражение как раз и соответствует признаку равномерной устойчивости. Что и требовалось доказать.
Терема 10.5 (признак неустойчивости). Если хотя бы для одного k коэффициент роста гармоники ρk нельзя мажорировать величиной 1 + Cτ, C = const, то разностная схема (10.30) неустойчива.
Доказательство. Пусть в начальный момент имеется ошибка вида εeikx для заданной гармоники k. Тогда к моменту t = mτ она возрастет в (ρk )m раз, что по модулю больше величины
(1 + Cτ)m = (1 + Cτ)t τ > Ct
τ > Ct
при сколь угодно большом C. Но неограниченный рост ошибки как раз и означает неустойчивость схемы.
Что и требовалось доказать.
Для разностной схемы (10.16) коэффициент роста гармоник определяется выражением (10.29). Поскольку функция sin2 (kh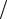 2) может изменяться в пределах от 0 до 1, наименьшее значение коэффициента роста гармоник
2) может изменяться в пределах от 0 до 1, наименьшее значение коэффициента роста гармоник
ρk =1 − 4τη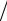 h2
h2
иможет стать меньше –1. Его значение ограничивается в соответствии с требованием теоремы 10.4:
ρk = 1 − 4τη h2 ≤1.
Отсюда получается:
−1 ≤1 − 4τη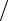 h2 ≤1, 4τη
h2 ≤1, 4τη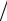 h2 ≤ 2 ,
h2 ≤ 2 ,
1 Согласно [8] под l2 понимается эвклидово пространство ∞-мерных векторов
∞
a = (a0 , a1 ,…) со скалярным произведением (a,b) = ∑ak bk
k =0
∞
и нормой 
 a
a
 2 = ∑ak2 .
2 = ∑ak2 .
k =0

τ ≤ h2  2η,
2η,
что соответствует полученному ранее с помощью принципа максимума условию устойчивости по начальным данным (пример 10.3).
10.4.3. Сходимость разностного решения
Разностная схема (10.20) корректна, если ее решение существует и единственно при любых входных данных, а сама разностная схема является устойчивой.
Разностное |
|
решение uh задачи (10.20) сходится к решению u зада- |
чи (10.19), если |
|
|
|
u |
h |
− u |
|
|
|
→0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
h→0 |
|
|
|
|
|
|
|
Теорема 10.6. Если решение u задачи (10.19) существует, разностная схема (10.20) корректна и аппроксимирует задачу (10.19) на данном решении, то разностное решение сходится к точному1.
Доказательство. Используя введенное ранее определение аппроксимации, можно определить величины погрешностей аппроксимации
ψh = Ahu − fh , |
|
|
|
|
|
|
|
|
|
|
= R u |
− ϕ |
|
. |
ν |
h |
|
|
h |
|
h |
|
|
Отсюда следует, что |
|
|
|
|
|
|
|
Ahu = fh + ψh , |
|
|
|
|
|
|
|
|
|
|
|
|
+ ν |
|
|
. |
R u = ϕ |
h |
h |
|
h |
|
|
|
Но теперь решение u можно рассматривать как возмущенное по сравнению с uh решение задачи (10.20), соответствующее внесенным возмущенииям ψh правой части и νh краевых условий. В силу предположения об устойчивости разностной схемы имеет место утверждение:
ε > 0 δ(ε)> 0, 
 uh − u
uh − u
 < ε,
< ε,
как только
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψh |
|
|
|
< δ(ε), |
|
|
|
νh |
|
|
|
|
|
< δ(ε). |
|
|
|
|
|
|
|
С другой стороны, в силу свойств аппроксимации |
δ > 0 h0 (δ)> 0, |
|
|
ψh |
|
|
|
< δ, |
|
|
|
νh |
|
|
|
< δ |
|
|
|
|
|
|
|
|
при h < h0 . Отсюда следует, что
1 «Сокращенная» форма теоремы: из аппроксимации и устойчивости следует сходимость разностного решения.

ε > 0 h0 [δ(ε)]> 0, 
 uh − u
uh − u
 < ε, h < h0 .
< ε, h < h0 .
Что и требовалось доказать.
Этим определяется порядок проведения исследования разностных схем: при выполнении условий аппроксимации, устойчивости и разрешимости разностной схемы (10.20) получаемое численное решение будет сходиться к точному решению поставленной краевой задачи (10.19).
Теорема 10.7. Если условия предыдущей теоремы выполнены, операторы Ah и Rh линейные, порядок погрешности аппроксимации равен p, то погрешность решения имеет порядок не ниже p.
Доказательство. Условие устойчивости представляется в виде
|
u1 − u2 |
|
|
|
≤ M 0 |
|
|
|
f1 − f2 |
|
|
|
+ M1 |
|
|
|
ϕ1 − ϕ2 |
|
|
|
. |
(10.32) |
|
|
|
|
|
|
|
|
|
|
|
Используя определение погрешности решения zh = uh −u ,
можно представить выражения (10.20) выражениями
Ah zh |
= ψh , |
|
|
|
|
|
|
|
|
|
= ν |
|
. |
R z |
h |
h |
|
h |
|
|
Применяя к ним формулу (10.32), можно получить

 zh
zh 
 ≤ M 0
≤ M 0 
 ψh
ψh 
 + M1
+ M1 
 νh
νh 
 .
.
В силу условия теоремы

 ψh
ψh 
 ≤ α0h p ,
≤ α0h p , 
 νh
νh 
 ≤ α1h p ,
≤ α1h p ,
откуда следует, что

 uh − u
uh − u
 ≤ Mh p , M = α0 M 0 + α1M1 .
≤ Mh p , M = α0 M 0 + α1M1 .
Что и требовалось доказать.
Контрольные вопросы и задания
10.1.Запишите условия согласования начальных (10.3) и граничных (10.5) (или (10.6)) условий для задачи (10.2).
10.2.Запишите условия согласования начальных (10.8) и граничных (10.9) условий для задачи (10.7).
10.3.Покажите, как с помощью замены переменных задачу (10.2)–(10.4) можно свести к задаче с однородными граничными условиями (10.13).
10.4.Укажите условия, при которых решение задачи (10.13) можно представлять в форме (10.14).
10.5.Проверьте порядок погрешности аппроксимации граничного условия (10.5) явным разностным аналогом (10.21) относительно шагов интегрирова-
ния τ и h.
10.6.Следует ли из равномерной устойчивости разностной схемы, что она устойчива и в обычном смысле?
10.7.Следует ли равномерная устойчивость разностной схемы из устойчивости в обычном смысле?
10.8.Укажите смысл коэффициента C в условии устойчивости (10.25).
10.9.Оцените порядок погрешности аппроксимации граничного условия (10.5) неявным вариантом схемы (10.21).
11. СЕТОЧНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ 11.1. Уравнения первого порядка
Рассматривается одномерный перенос потоком жидкости или газа (например, в прямолинейной трубке) частицы, состояние которой определяется функцией u(t, x), то есть зависит от времени t и ее положения x. Скорость изменения состояния частицы (в эйлеровой системе отсчета) определяется полной производной по времени,
du dt = ut′ + u′x dx
dt = ut′ + u′x dx dt = ut′ + vu′x ,
dt = ut′ + vu′x ,
v – cкорость перемещения частицы, которая для упрощения считается постоянной в течение всего исследуемого периода [0, T]. Если скорость изменения состояния частицы f (t, x) известна, то простейшее уравнение переноса (диффе-
ренциальное уравнение первого порядка) имеет вид |
|
ut′ + vu′x = f (t, x). |
(11.1) |
В качестве условий для определения постоянных интегрирования прини- |
маются начальные (t = 0) и граничные (x = 0) условия: |
|
u(0, x)=U (x), |
|
|
(11.2) |
|
u(t,0)=U 0 (t). |
|
|
|
Естественно потребовать выполнение условий сопряжения U (0) = U 0 (0). Фактически речь идет о смешанной задаче Коши, поскольку заданы начальные условия по обеим независимым переменным.
11.1.1. Схемы бегущего счета
Рассматривается задача (11.1)–(11.2) в области
G = [0, T ]×[0, L],
для которой используется разностная сетка
Ω ={(ti , xj ) ti = iτ, i = 0,m; xj = jh, j = 0,n} , m =T τ, n = L h .
Дифференциальное уравнение (11.1) аппроксимируется на простейшем шаблоне (рис. 11.1, а). Разностное соотношение для дифференциального уравнения (11.1) записывается в виде
(u j − u j ) τ + ν(u j− u j−1 ) h = f . |
(11.3) |
249
Выражение, стоящее в правой части этого соотношения, вычисляется для центра ячейки (на рис. 11.1, а, отмечено символом ×):
~ |
= f (ti + τ 2, x j − h 2). |
f |
Для определения свойств разностной схемы (11.3) и оценки порядка погрешности аппроксимации этой схемой дифференциального уравнения (11.1) решение и правая часть разлагаются в ряды Тейлора:
u(ti+1, x j )= u(ti , x j )+ ut′(ti , x j )τ + utt′′(ti , x j )τ2  2 + O(τ3 ),
2 + O(τ3 ),
u(ti , x j−1 )= u(ti , x j )− u′x (ti , x j )h + u′xx′ (ti , x j )h2 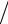 2 + O(h3 ),
2 + O(h3 ),
f (ti+1 2 , x j−1 2 )= f (ti , x j )+ ft′(ti , x j )τ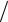 2 − fx′(ti , x j )h
2 − fx′(ti , x j )h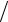 2 + O(τ2 ,h2 ).
2 + O(τ2 ,h2 ).
i + 1
i
x |
x |
x |
j – 1 j j + 1 |
j – 1 j j + 1 |
j – 1 j j + 1 |
а |
б |
в |
t |
t |
|
j – 1 j j + 1 |
j – 1 j j + 1 |
г |
д |
Рис. 11.1. Варианты шаблонов для аппроксимации уравнения переноса
Погрешность аппроксимации разностной схемой дифференциального уравнения
ψij = [u(ti+1, x j )− u(ti , x j )]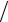 τ + v[u(ti , x j )− u(ti , x j−1 )]
τ + v[u(ti , x j )− u(ti , x j−1 )] h − f (ti+1 2 , x j−1 2 )= = ut′(ti , x j )+ utt′′(ti , x j )τ
h − f (ti+1 2 , x j−1 2 )= = ut′(ti , x j )+ utt′′(ti , x j )τ 2 + vu′x (ti , x j )− vu′xx′ (ti , x j )h
2 + vu′x (ti , x j )− vu′xx′ (ti , x j )h 2 −
2 −









 dt = ut′ + u′x dx
dt = ut′ + u′x dx dt = ut′ + vu′x ,
dt = ut′ + vu′x ,


 δθ
δθ
 δθ
δθ


 , а
, а 


 :
:

 δθ
δθ
 ≤
≤ 
 δ
δ
 +
+ 
 δθ
δθ

 τ
τ τ +
τ + 
 τ
τ τ +
τ + 
 τ
τ τ +
τ + 
 τ = η
τ = η
 τ
τ
 τ −
τ − 
 τ −
τ − 
 τ ≥ ω
τ ≥ ω τ
τ τ = η
τ = η

 δθ
δθ


 δθ
δθ


 δθ
δθ


 δθ
δθ


 2
2








 < ε
< ε


 < ε
< ε


 ≤
≤ 
 ψ
ψ
 +
+ 
 ν
ν


 ψ
ψ
 ≤ α
≤ α
 ν
ν
 ≤ α
≤ α


 ≤
≤