
Методы вычислительной математики
..pdf
из которого следует, что для различных собственных значений, λi ≠ λ j , собст-
венные векторы матриц A и AT взаимно ортогональны.
Выражение (5.1) записывается в малых приращениях
δAX (i ) + AδX (i) = δλi X (i) + λiδX (i).
и скалярно умножается на Y ( j ):
(δAX (i),Y ( j ) )+ (AδX (i),Y ( j ) )= (δλi X (i ),Y ( j ) )+ (λiδX (i),Y ( j ) ). |
(5.4) |
Для оценки устойчивости собственных значений первоначально в формуле (5.4) полагается i = j:
(δAX (i),Y (i ) )+ (AδX (i),Y (i ) )= δλi (X (i ),Y (i) )+ λi (δX (i ),Y (i) ).
Поскольку
(AδX (i ),Y (i) )= (δX (i ), AT Y (i ) )= (δX (i ),λiY (i ) )= λi (δX (i ),Y (i) ),
из последнего равенства получается
(δAX (i ),Y (i) )= δλi (X (i),Y (i ) ),
откуда следует
δλi 
 (X (i),Y (i) ) = (δAX (i),Y (i) ) ≤
(X (i),Y (i) ) = (δAX (i),Y (i) ) ≤ 
 δAX (i )
δAX (i ) 


 Y (i)
Y (i) 
 ≤
≤ 
 δA
δA


 X (i)
X (i) 


 Y (i )
Y (i ) 

Это позволяет получить оценку
|
δλi |
|
≤ |
|
|
|
|
|
|
δA |
|
|
|
|
|
|
X (i) |
|
|
|
|
|
|
|
|
|
|
Y (i ) |
|
|
|
|
|
(X (i ),Y (i) ) |
|
= Ci |
|
|
|
δA |
|
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
Величина |
|
|
|
(X (i ),Y (i ) ) |
|
=1 cos(ϕi ) |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Ci = |
|
|
|
X (i) |
|
|
|
|
|
|
|
Y (i ) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
называется коэффициентом перекоса; ϕi – угол между векторами
.
X (i) и Y (i ).
В дальнейшем предполагается, что матрица A симметрична1, A = AT , и все ее собственные числа различны. В этом случае собственные векторы матрицы А образуют в Rm полную ортонормированную систему, которую можно использовать в качестве базиса. Очевидно, что для симметричных матриц X (i) =Y (i ) . Следовательно, имеет место устойчивость собственных значений:
δλi ≤ 
 δA
δA
 .
.
Для получения оценки устойчивости собственных векторов рассматривается случай i ≠ j в формуле (5.4). Использование равенства
(AδX (i ),Y ( j ) )= (δX (i ), AT Y ( j ) )= (δX (i ),λ jY ( j ) )= λ j (δX (i ),Y ( j ) )
1 Вэтомслучае, согласномонографии[9], всесобственныечисламатрицыА– вещественные.
121

и условия ортогональности векторов
(X (i),Y ( j ) )= 0, i ≠ j ,
в соотношении (5.4) приводит к выражению
(δAX (i),Y ( j ) )= λi (δX (i ),Y ( j ) )− λ j (δX (i),Y ( j ) ),
откуда следует
(δX (i ),Y ( j ) )= (δAX (i ),Y ( j ) )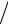 (λi − λ j ).
(λi − λ j ).
Вектор δX (i) может быть разложен по базису X (k ), k =1,m :
|
|
|
m |
|
|
δX (i ) = ∑δαik X (k ) . |
|
|
|
|
k =1 |
Подстановка этого разложения в скалярное произведение, |
|||
|
m |
|
m |
(δX (i),Y ( j ) )= |
∑δαik X (k ),Y ( j ) |
= ∑δαik (X (k ),Y ( j ) )= δαij (X ( j ),Y ( j ) ), |
|
k=1 |
|
k=1 |
|
позволяет получить формулу для коэффициентов разложения:
δαij = (δX (i ),Y ( j ) ) (X ( j ),Y ( j ) )= (δAX (i ),Y ( j ) ) (X ( j ),Y ( j ) )(λi − λ j ), |
i ≠ j . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В случае i = j за счет произвола в выборе длины собственных векторов |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
можно |
положить |
|
δαij = 0 . |
|
|
|
|
|
Тогда |
|
|
|
|
разложение вектора δX (i) |
по бази- |
|||||||||||||||||||||||||||||||||||||||||||||
су X (k ), |
k = |
|
|
, имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1,m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
δX (i ) = ∑m (δAX (i),Y (k ) )X (k ) (X (k ),Y (k ) )(λi − λk ). |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
k =1,k≠i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Приращение вектора δX (i) оценивается неравенством |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(X (k ),Y (k ) ) λi − λk = |
|
||||||||||||
|
|
|
δX (i ) |
|
≤ ∑ |
|
|
|
δA |
|
|
|
|
|
|
|
|
|
X (i) |
|
|
|
|
|
|
|
|
|
Y (k ) |
|
|
|
|
|
|
|
X (k ) |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
k=1,k≠ |
i |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(X (k ) ,Y (k ) ) λi − λk , |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
= |
|
δA |
|
|
|
X (i ) |
|
|
|
|
|
∑ |
Y |
|
|
(k ) |
|
X (k ) |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =1,k ≠ |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
||||
|
|
|
|
|
|
|
|
|
δX (i ) |
|
|
|
|
|
|
|
≤ |
|
|
|
δA |
|
|
|
X (i) |
∑Ck |
λi − λk . |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=1,k≠i |
|
|
|||||
Отсюда следует, что неустойчивость собственных векторов имеет место в случае, когда велики коэффициенты перекоса Ck либо близки собственные
значения λk , k =1,m .
|
2 |
|
1 |
. |
|
Пример 5.2. Определить коэффициенты перекоса матрицы A = |
|
|
5 |
4 |
|
|
|
|
122
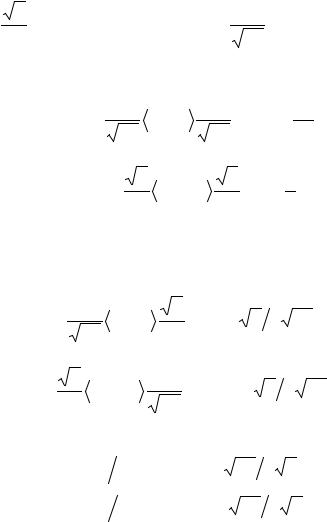
Для транспонированной матрицы
1 |
5 |
AT = |
|
2 |
4 |
|
|
собственные числа сохраняются: λ1 = 6, λ2 = −1 (см. пример 5.1); компоненты |
||||||||||||||
собственных векторов принимают следующие значения: |
|
|||||||||||||
|
2 |
1 |
0,707107 |
|
|
1 |
− 5 |
|
0,928477 |
|||||
Y (1) = |
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
= |
|
, Y (2) = |
|
29 |
|
= |
. |
|||||
|
1 |
0,707107 |
|
|
|
2 |
|
|
0,371391 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скалярные произведения собственных векторов обеих матриц |
|
|||||||||||||
|
(X (1),Y (2) )= |
1 |
|
1 |
|
− 5 |
|
|
1 |
|
|
|
||
|
2, 5 |
|
|
|
= |
|
0 = 0, |
|
||||||
|
29 |
29 |
|
2 |
|
29 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(X (2),Y (1) )= |
2 |
|
2 |
1 |
|
1 |
|
|
− 1, 1 |
|
= |
0 |
= 0, |
||||
2 |
2 |
|
2 |
|||||
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
подтверждают ортогональность собственных векторов матриц A и AT в случае
λi ≠ λk .
(X (1),Y (1) )= |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2, |
|
5 |
|
|
|
|
2 |
29 = 0,919145, |
||||||||||||||||||||||
|
|
|
|
|
|
|
29 |
|
2 |
= 7 2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(X (2),Y (2) )= |
2 |
|
|
|
|
|
|
|
|
|
|
1 |
− 5 |
|
|
|
|
|
|||||||||||||||||||
− |
1, |
|
|
|
|
1 |
|
|
|
|
|
= 7 |
|
2 |
2 29 = 0,919145. |
||||||||||||||||||||||
2 |
|
|
|
|
|
|
29 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты перекоса равны: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
C = |
|
|
|
X (1) |
|
|
|
|
|
|
Y (1) |
|
|
|
|
|
|
|
(X (1),Y (1) ) |
|
= 2 |
29 |
|
7 |
2 =1,087968, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(X (2),Y (2) |
|
) |
|
|
|
|
|
|
|
||||
C2 = |
|
|
|
X (2) |
|
|
|
|
|
Y (2) |
|
|
|
|
|
|
|
|
|
= 2 |
29 |
7 |
2 =1,087968. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Пример 5.3. Оценить влияние погрешности на результаты вычисления |
|||||||||||||||||||||||||||||||||||||
собственных значений матрицы |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
|
0 |
3 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
4 |
|
|
|
||||||
где ε – малое возмущение (погрешность).
123

Решение характеристического уравнения
det(A − λE)= (1 − λ)(2 − λ)(3 − λ)(4 − λ) − ε = 0 .
дает корни (собственные значения):
λ1 |
= 2,5 − |
5 + 4 |
1 + ε |
2 , |
λ2 |
= 2,5 − |
5 − 4 |
1 + ε |
2 , |
λ3 |
= 2,5 + |
5 − 4 |
1 + ε |
2 , |
λ4 |
= 2,5 + |
5 + 4 |
1 + ε |
2 . |
В табл. 5.1 приведены собственные значения исходной матрицы при различных величинах ε.
Таблица 5.1 Собственные значения матрицы при заданных погрешностях
Собственные |
ε = 0,1 |
ε = 0,01 |
ε = 0,001 |
ε = 0 |
|
значения |
|||||
|
|
|
|
||
|
|
|
|
|
|
λ1 |
0,983818 |
0,998338 |
0,999833 |
1,0 |
|
λ2 |
2,051457 |
2,005013 |
2,000500 |
2,0 |
|
λ3 |
2,948543 |
2,994987 |
2,999499 |
3,0 |
|
λ4 |
4,016182 |
4,001662 |
4,000167 |
4,0 |
5.2. Определение собственных значений методом интерполяции
Задана матрица А размером m × m. Характеристический многочлен в этом случае имеет порядок m (полином степени m), и задача заключается в определении корней этого характеристического полинома. Алгоритм вычисления собственных значений матрицы А:
1. Строится функция f (λ) = det(A − λE):
а) на числовой оси выбирается набор из m + 1 значений λk , k = 0,m ;
б) подсчитываются значения функции f (λk ), k = 0,m, например, с помощью метода Гаусса решения системы линейных алгебраических уравнений;
в) по найденным значениям f (λk ), k = 0,m, строится интерполяционный полином Pm (x) Ньютона (Лагранжа); ранее отмечалось, что для рассматриваемого случая многочлен степени m определяется единственным образом; в силу этого построенный полином как раз и будет характеристическим.
124

2. Каким-либо из известных методов решения нелинейных уравнений отыскиваются корни построенного полинома Pm (x), которые представляют собой собственные значения исходной матрицы.
5.3. Поиск собственных векторов
При численных расчетах, как правило, отыскиваются лишь приближенные
~ |
|
|
|
|
|
|
|
|
|
|
i =1,m . В этом случае |
||||||||||
величины собственных значений λi , |
||||||||||
|
|
~ |
|
|
|
|
|
|
||
det(A − λi E)≠ 0, |
|
|
|
|
|
|||||
и система уравнений |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(A − λi E)X (i) = 0 |
|
|
|
|
|
|||||
позволяет отыскать лишь тривиальное решение X (i) = 0, |
i = |
|
. |
|
|
|||||
1,m |
||||||||||
С использованием произвольного вектора F Rm |
формируется система |
|||||||||
алгебраических уравнений |
|
|
|
|
|
|
|
|
|
|
~ |
|
(0) |
= F. |
(5.5) |
||||||
(A − λi E)Z |
|
|||||||||
В Rm собственные линейно-независимые векторы |
X (k ), k = |
|
, соответ- |
|||||||
1,m |
||||||||||
ствующие различным собственным значениям1, можно использовать в качестве базиса и построить разложения векторов Z (0) и F по этому базису:
m
Z (0) = ∑α(k0) X (k ) , k=1
m
F = ∑βk X (k ).
k=1
Эти выражения подставляются в систему уравнений (5.5):
~ |
m |
m |
|
|
|
(A − λi E)∑α(k0) X (k ) = ∑βk X (k ), |
||
|
k=1 |
k=1 |
m [ (0)
∑ αk
k=1
m[
=∑ α
k=1
~ |
m |
|
~ |
|
|
||
(A − λi E)X (k ) |
− βk X (k ) ]= ∑[α(k0) (AX (k ) − λi X (k ) )− βk X (k ) ]= |
||
|
k=1 |
|
|
~ |
|
m |
~ |
(k0) (λk X (k ) − λi X (k ) )−βk X (k ) ]=∑[α(k0) (λk − λi )−βk ]X (k ) = 0.
k=1
В силу линейной независимости векторов базиса получается:
αk (λk − λi )− βk = 0 , |
αk =βk (λk − λi ), k =1,m . |
|||||
(0) |
~ |
(0) |
~ |
|
|
|
При условии, |
~ |
коэффициент |
(0) |
становится большим, |
||
что λi ≈ λi , |
αi |
|||||
αi(0) >> α(k0) , k ≠ i , вследствие чего
1 Согласно монографии [9] собственные векторы, соответствующие попарно различным собственным значениям, линейно независимы.
125

m
Z (0) = ∑α(k0) X (k ) ≈ αi(0) X (i ) , k=1
то есть вектор Z (0) будет близок по направлению к собственному вектору X (i) . Повторяя решение системы уравнений (5.5) с новой правой частью,
(A − λi E)Z |
(1) |
= Z |
(0) |
, |
~ |
|
|
вновь представляя решение в виде разложения по базису X (k ), k =1,m ,
m
Z (1) = ∑α(k1) X (k ) ,
k=1
иповторяя предыдущие рассуждения, можно получить выражение
|
αk |
= αk |
(λk − λi ), k =1,m . |
||
|
(1) |
(0) |
~ |
|
|
Поскольку коэффициент αi(0) значительно преобладает над остальными |
|||||
коэффициентами α(k0) , |
k ≠ i , |
новый коэффициент αi(1) будет еще больше, чем |
|||
αi(0) , то есть вектор Z (1) |
будет еще ближе по направлению к собственному век- |
||||
тору X (i) . Иными словами, для нахождения собственного вектора X (i) можно построить итерационный процесс вида
~ |
|
(5.6) |
(A − λi E)Z (s+1) = Z (s) , |
|
|
причем Z (0) – произвольный начальный вектор. Следует отметить, |
что если |
|
собственное значение вычислено достаточно точно, то |
~ |
, что мо- |
det(A − λi E)≈ 0 |
||
жет привести к аварийной остановке вычислительного процесса. В этом случае
для повышения устойчивости расчетов в матрицу |
~ |
следует внести по- |
||
A − λi E |
||||
|
|
~ |
|
|
грешность, например за счет искажения собственного значения λi . |
|
|
||
|
|
|
2 |
|
|
|
1 |
. |
|
Пример 5.4. Определить собственные векторы матрицы A = |
|
|||
|
|
5 |
4 |
|
|
|
|
|
|
В примере 5.1 получены собственные значения λ1 = 6, λ2 = −1. Для определения собственных векторов, соответствующих первому собственному зна-
~
чению, вводится погрешность ε: λ1 = λ1 + ε = 6 + ε. Система уравнений (5.6) для
1
первого вектора Z (0) = принимает вид
1
126
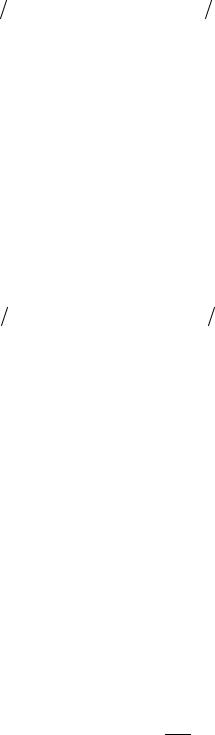
− (5 + ε)X |
(1) + 2X (1) =1, |
||
|
1 |
2 |
|
|
|
+ ε)X (1) =1. |
|
5X (1) − (2 |
|||
|
1 |
2 |
|
Эта система уравнений имеет решение: |
|
||
X1(1) = − (4 + ε) ε(7 + ε), X 2(1) = − (10 + ε) ε(7 + ε). |
|||
Для погрешности ε = 0,001 получается: |
|
||
X1(1) = −571,4898, |
X 2(1) |
= −1428,510, |
|

 X (1)
X (1) 
 =1538,584.
=1538,584.
После нормирования первый собственный вектор имеет компоненты
X1(1) = −0,371439, X 2(1) = −0,928458.
Такая же процедура выполняется для второго собственного значения:
|
~ |
|
|
|
|
+ ε = ε −1; |
|||
|
λ2 = λ2 |
||||||||
(2 − ε)X (2) + 2X |
(2) |
=1, |
|||||||
|
1 |
|
2 |
|
|||||
|
|
|
|
|
|
|
|
(2) |
=1; |
5X (2) + (5 − ε)X |
|||||||||
|
1 |
|
|
|
|
|
2 |
|
|
X1(2) = (15 + 9ε) 5ε(7 + ε), X 2(2) = − (3 + ε) ε(7 + ε); |
|||||||||
X1(2) = 428,7673, |
X 2(2) = −428,6531; |
||||||||
|
|
X (2) |
|
|
|
= 606,2878 . |
|||
|
|
|
|
||||||
Нормированный второй собственный вектор:
X1(2) = 0,707201, X 2(2) = −0,707013.
Точные значения компонент обоих векторов определены в примере 5.1.
5.4. Частичная проблема собственных значений
В инженерной практике иногда возникает задача определения не всего спектра собственных значений и векторов, а лишь каких-то, например максимального и минимального собственных значений и соответствующих им векторов. В этом разделе рассматриваются простейшие способы вычисления собственных чисел и векторов. Для более глубокого знакомства с проблемой собственных значений следует обратиться к монографиям [19, 43].
5.4.1. Метод линеаризации
Рассматривается задача (5.1), представленная в компонентной форме:
m |
|
fi (X ,λ) = ∑aij X j − λX i = 0, i =1,m . |
(5.7) |
j=1
127

Полученное выражение можно рассматривать как систему m нелинейных уравнений с m + 1 неизвестными величинами λ и X j , j =1,m . Для замыкания системы уравнений добавляется условие нормирования собственного вектора:
fm+1 (X )= ∑m (X j )2 −1 = 0. |
(5.8) |
j=1 |
|
Использование метода Ньютона для решения системы нелинейных уравнений (5.7)–(5.8) приводит к итерационному процессу
fi (X (s) ,λ(s) )+ ∑m ∂fi (X (s) ,λ(s) ) X (js) + |
∂fi (X (s) ,λ(s) ) λ(s) = 0, i = |
|
, |
||
1,m |
|||||
j=1 |
∂X j |
|
∂λ |
||
fm+1 (X (s) )+ ∑m ∂fm+1 (X (s) ) X (js) = 0, |
|||||
|
j=1 |
∂X j |
|||
где X (js) = X (js+1) − X (js) , |
λ(s) = λ(s+1) |
− λ(s ) , |
s – номер итерации. Для уравнений |
||
(5.7) и (5.8) итерационная процедура метода Ньютона принимает вид
m
∑a X (s)
ij j
j=1
m ( )
∑ X (js) 2
j=1
m |
|
||
− λ(s) X i(s) + ∑aij X (js) − λ(s) X i(s) − X i(s) |
λ(s) = 0, |
||
j=1 |
(5.9) |
||
m |
|||
−1 + 2∑ X (js) X (js) = 0, i = |
|
. |
|
1,m |
|
||
j=1 |
|
||
В результате такого итерационного процесса будет найдено какое-то собственное значение и соответствующий ему собственный вектор, зависящие от начального приближения.
|
2 |
|
1 |
. |
|
Пример 5.5. Определить собственные векторы матрицы A = |
|
|
5 |
4 |
|
|
|
|
Согласно формулам (5.9) строится итерационная процедура для вычисления собственного значения и вектора:
|
X (s) + 2 X (s) |
− |
X (s) |
λ(s) − λ(s) |
X (s) = λ(s) X (s) − X (s) − |
2X (s) ; |
|
||||||
|
1 |
2 |
|
|
1 |
λ |
− λ |
1 |
= λ |
1 |
1 |
2 |
; |
5 |
X1 |
+ 4 X 2 |
|
− X 2 |
X 2 |
X 2 |
− 5X1 |
− 4X 2 |
|||||
|
(s) |
(s) |
|
(s) |
(s) |
(s) |
(s) |
(s) |
(s) |
(s) |
(s) |
|
|
|
|
X1(s) + 2X 2(s) X 2(s) =1 − (X1(s) )2 − (X 2(s) )2 ; |
|
|
|
||||||||
2X1(s) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
128

(1 |
− λ(s) ) X |
(s) + 2 |
X (s) − X (s) |
λ(s) = λ(s) X (s) − X (s) |
− 2X (s) |
; |
|||
|
1 |
2 |
1 |
1 |
1 |
|
2 |
|
|
5 |
X (s) + (4 |
− λ(s) ) |
X (s) − X (s) |
λ(s) = λ(s) X (s) − 5X (s) − |
4X (s) ; |
||||
|
1 |
|
2 |
2 |
2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2X1(s) |
X1(s) + 2X 2(s) X 2(s) =1 − (X1(s) )2 − (X 2(s) )2 . |
|
|
На каждом этапе расчетов очередное s + 1 приближение решения определяется по формулам
X1(s+1) |
= X1(s) + |
X1(s) , |
X 2(s+1) |
= X 2(s) + |
X 2(s) , |
λ(s+1) = λ(s) + λ(s) .
Результаты расчетов сведены в табл. 5.2.
Таблица 5.2 Определение собственного значения и соответствующего ему вектора
Номер итерации |
X1(s) |
X 2(s) |
λ(s) |
0 |
1,0 |
1,0 |
1,0 |
|
|
|
|
1 |
–0,375 |
1,875 |
4,75 |
|
|
|
|
2 |
0,457419 |
1,082795 |
6,268627 |
|
|
|
|
3 |
0,376979 |
0,946529 |
6,038836 |
|
|
|
|
4 |
0,371427 |
0,928556 |
6,000516 |
|
|
|
|
5 |
0,371391 |
0,928477 |
6,0 |
|
|
|
|
6 |
0,371391 |
0,928477 |
6,0 |
|
|
|
|
Найденное решение сосоответствует найденному в примере 5.1 собственному значению λ1 и собственному вектору X (1) .
5.4.2. Степенной метод
Степенной метод предназначен для определения наибольшего (по модулю) собственного значения. Предполагается, что все собственные числа упорядочены следующим образом:
λ1 > λ2 >…> λm .
Рассматривается итерационный процесс
Z (s+1) = AZ (s) .
Начальное приближение Z (0) представляется разложением по базису, построенному из собственных векторов X (k ), k =1,m, матрицы A:
129
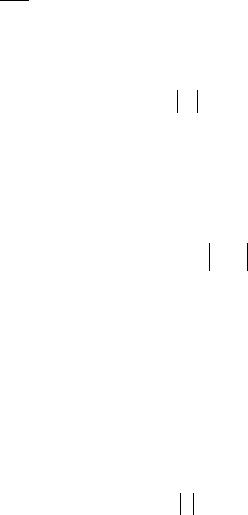
m
Z (0) = ∑αk X (k ). k=1
Определяются приближения в соответствии с формулой итерационного процесса:
m |
m |
m |
m |
|
|
|
|
|
|
||
Z (1) = AZ (0) = A∑αk X (k ) = ∑αk (AX (k ) )= ∑αk (λk X (k ) )= |
∑αk λk X (k ); |
|
|
||||||||
k=1 |
k=1 |
k=1 |
k=1 |
|
|
|
|
|
|
||
|
m |
m |
|
|
|
|
|
|
|
|
|
Z (2) = AZ (1) |
= ∑αk λk AX (k ) = ∑αk (λk )2 X (k ) ; |
|
|
|
|
|
|
||||
|
k=1 |
k=1 |
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
Z (s) = ∑αk (λk )s X (k ). |
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
Для достаточно большого числа итераций получается, |
что |
|
λ1 |
|
s >> |
|
λk |
|
s , |
||
|
|
|
|
||||||||
k = 2,m . Отсюда следует, что Z (s) ≈ α1 (λ1 )s X (1) , то есть построенная указанным способом последовательность векторов Z (0) , Z (1) , Z (2) ,… сходится (с точностью
до направления) к собственному вектору X 1 , соответствующему наибольшему собственному значению λ1 . Кроме того, учитывая, что имеет место зависимость
Z (s+1) ≈ α1 (λ1 )s+1 X (1) = λ1[α1 (λ1 )s X (1) ]≈ λ1Z (s), |
(5.10) |
итерационный процесс позволяет вычислить наибольшее (по модулю) собственное значение:
λ(1s+1) = 
 Z (s+1)
Z (s+1) 

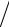

 Z (s)
Z (s) 
 .
.
5.4.3. Метод обратных итераций
Для нахождения наименьшего (по модулю) собственного значения матрицы А можно воспользоваться тем, что матрица A−1 имеет собственные значения, обратные собственным значениям матрицы А. В этом случае итерационный процесс
Z (s+1) = A−1Z (s) |
(5.11) |
|||
позволяет определить модуль наибольшего собственного числа |
|
μ |
|
матри- |
|
|
|||
цы A−1 . Соответственно, μ −1 является наименьшим (по модулю) собственным числом матрицы A.
130
