
Методы вычислительной математики
..pdf
3. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ1
Предполагается, что задана нелинейная зависимость f(x). Требуется опре-
делить все те значения аргумента |
~ |
k = 1, 2, …, которые обращают функцию |
xk , |
||
в нуль: |
|
|
(3.1)
Для поиска корней нелинейных уравнений, как правило (за небольшим исключением: квадратные, кубические, некоторые трансцендентные уравнения), используются итерационные методы.
3.1. Метод половинного деления2
Метод основан на теореме математического анализа [2]: функция, непрерывная в замкнутом интервале и принимающая на концах этого интервала значения разных знаков, хотя бы один раз обращается в нуль внутри интервала.
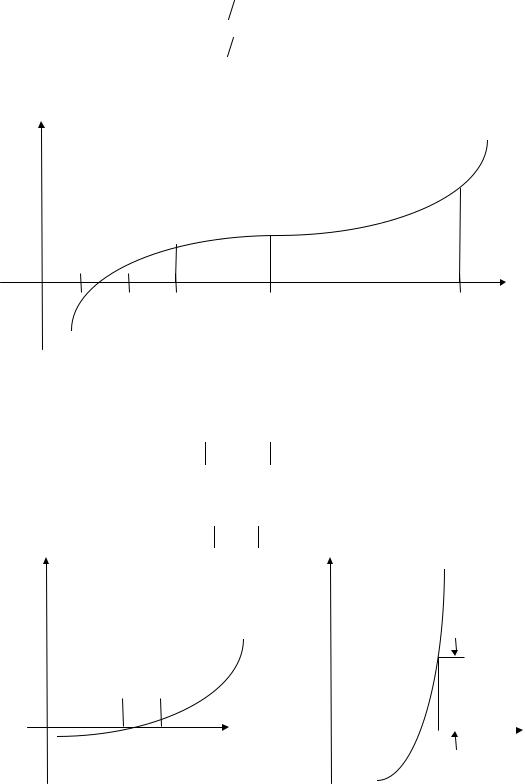
Пусть функция f(x) непрерывна на отрезке [x0 , x1 ]. Процедура метода заключается в последовательном сокращении длины отрезка для локализации корня уравнения (3.1). Первоначально проверяются значения заданной функции на концах отрезка. В случае, если
f (x0 ) f (x1 )= 0 ,
один из концов отрезка является искомым корнем уравнения.
Пусть на концах отрезка значения функции имеют разные знаки, то есть имеет место соотношение
|
f (x0 ) f (x1 )< 0. |
отрезка, x2 = (x0 + x1 ) 2, |
Вычисляется значение аргумента в середине |
||
и вычисляется значение функции f (x2 ) в этой точке. Далее сравниваются зна- |
||
ки функции в точке x2 |
и, например, в левой точке x0 |
отрезка. Если имеет место |
соотношение f (x0 ) f |
(x2 )< 0 (рис. 3.1), то корень следует искать на отрезке |
|
[x0 , x2 ]. В противном случае корень разыскивается на отрезке [x2 , x1 ]. В резуль-
тате выполненной операции исходный отрезок сократился вдвое. Далее, в зависимости от ситуации, отрезок вновь делится пополам,
1Дополнительно методы решения нелинейных уравнений рассматриваются в разделе, посвященном интерполяции функций.
2Встречаются иные названия этого метода – метод бисекции, дихотомии.
71
|
(x2 + x0 ) |
||
x3 |
|
|
|
= |
|
+ x ) |
|
|
(x |
2 |
|
|
|
1 |
|
2, f (x2 ) f (x0 )< 0; 2, f (x2 ) f (x0 )> 0,
и так далее. Для прекращения вычислительной процедуры могут применяться различные критерии.
f(x4) f(x3)
f(x1)
f(x2)
x0 |
x4 |
x3 |
x2 |
x1 |
Рис. 3.1. Схема метода половинного деления
Если функция достаточно «пологая», имеет смысл использовать условие малости интервала, ограничивающего положение корня (рис. 3.2, a):
xs+1 − xs < δx ;
Если функция «круто» меняет свое значение, целесообразно применять условие (рис. 3.2, б) «близости» значения функции f(x) к нулевому значению:
f (xs ) < δy .
δy
 δx
δx 
|
xs+1 |
|
xs |
xs |
|
a |
|
б |
Рис. 3.2. Частные случаи поиска корня нелинейного уравнения
Если заранее неизвестен характер «поведения» функции, имеет смысл использоватьодновременнообаусловиядляостановкиитерационногопроцесса.
72
Пример 3.1. Найти корень уравнения 2x + sin(x)− 1 = 0 .
Вид функции f (x) = 2x + sin(x)−1 показан на рис. 3.3, из которого видно, что корень этого уравнения принадлежит отрезку [0, 1]. Рассматриваемая
Рис. 3.3. Функция f (x) = 2x + sin(x)− 1
функция на этом отрезке непрерывна и на его концах принимает значения разных знаков. Это означает, что для поиска корня заданного уравнения может быть использован метод половинного деления. Результаты расчетов приведены в табл. 3.1. Точное значение корня уравнения: 0,335418.
Таблица 3.1 Результаты вычисления корня уравнения 2x + sin(x) −1 = 0
методом половинного деления
Номер |
Левая точка |
Средняя точка |
Правая точка |
Ширина |
итерации |
отрезка |
|||
|
|
|
|
|
1 |
0,0 |
0,5 |
1,0 |
1,0 |
2 |
0,0 |
0,25 |
0,5 |
5,0 10–1 |
3 |
0,25 |
0,375 |
0,5 |
2,5 10–1 |
4 |
0,25 |
0,3125 |
0,375 |
1,25 10–1 |
5 |
0,3125 |
0,34375 |
0,375 |
6,25 10–2 |
6 |
0,3125 |
0,328125 |
0,34375 |
3,125 10–2 |
7 |
0,328125 |
0,3359375 |
0,34375 |
1,5625 10–2 |
8 |
0,328125 |
0,3320313 |
0,3359375 |
7,8125 10–3 |
9 |
0,3320313 |
0,3339844 |
0,3359375 |
3,9063 10–3 |
10 |
0,3339844 |
0,3349609 |
0,3359375 |
1,9531 10–3 |
11 |
0,3349609 |
0,3354492 |
0,3359375 |
9,7656 10–4 |
12 |
0,3349609 |
0,3352051 |
0,3354492 |
4,8828 10–4 |
73
Окончание табл. 3.1
Номер |
Левая точка |
Средняя точка |
Правая точка |
Ширина |
итерации |
отрезка |
|||
|
|
|
|
|
13 |
0,3352051 |
0,3353271 |
0,3354492 |
2,4414 10–4 |
14 |
0,3353271 |
0,3353882 |
0,3354492 |
1,2207 10–4 |
15 |
0,3353882 |
0,3354187 |
0,3354492 |
6,1035 10–5 |
|
|
… |
|
|
36 |
0,3354180 |
0,3354180 |
0,3354180 |
2,9104 10–11 |
37 |
0,3354180 |
0,335418032 |
0,3354180 |
1,4552 10–11 |
3.2. Метод простых итераций
Этот метод заключается в замене уравнения (3.1) эквивалентным ему урав-
нением вида |
|
x = ϕ(x). |
(3.2) |
Строится итерационный процесс |
|
x(s+1) = ϕ(x(s) ) |
(3.3) |
при некотором заданном начальном значении x(0) . Для приведения выражения (3.1) к требуемому виду (3.2) можно воспользоваться простым приемом:
f(x) = f (x) + x − x = 0 ,
x= x − f (x) = ϕ(x).
Если положить ϕ(x) = x − τf (x), выражение (3.2) можно записать в виде стандартного итерационного процесса поиска корней нелинейного уравнения:
(x(s+1) − x(s) )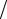 τ(s+1) + f (x(s) ) = 0 .
τ(s+1) + f (x(s) ) = 0 .
Теорема 3.1. Если функция ϕ(x) на отрезке А удовлетворяет условию Липшица1 с константой 0 < С < 1, причем
|
|
|
|
|
|
|
ϕ(a)− a |
|
≤ (1 − C)r , |
|
|
|
~ |
(3.4) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
то уравнение (3.2) имеет на отрезке А единственное решение |
, метод простой |
|||||||||||||||||||||||||
x |
||||||||||||||||||||||||||
итерации x |
(s+1) |
= ϕ(x |
(s) |
|
|
|
|
|
~ |
при любом |
x |
(0) |
A и имеет место оценка |
|||||||||||||
|
|
) сходится к x |
|
|||||||||||||||||||||||
|
|
|
|
|
|
x |
(n) |
~ |
|
≤ C |
n |
|
x |
(0) |
~ |
|
. |
|
|
|
|
(3.5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
− x |
|
|
|
|
− x |
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||||||||||||||||
|
1 Липшиц Рудольф Отто Сигизмунд |
|
[14.5.1832 – 7.10.1903] – немецкий математик. |
|||||||||||||||||||||||
С 1864 года являлся профессором Боннского университета. В 1900 году избран членом- |
||||||||
корреспондентом Парижской академии наук. |
||||||||
|
Функция удовлетворяет |
условию Липшица на отрезке [a, b], если x1 , x2 [a, b] |
||||||
|
ϕ(x2 )−ϕ(x1 ) |
|
≤ C |
|
x2 − x1 |
|
, C > 0 |
– константа, [8]. |
|
|
|
|
|||||
74

Рассматривается отрезок длиной 2r с центром в точке a: A = {x | x − a | ≤ r}. Доказательство. Доказывается «по индукции», что определяемые в соот-
ветствии с формулой (3.3) величины |
x(s) A s . Действительно, x(0) A по |
условию теоремы. Предполагается, |
что x(s) A . Следует показать, что |
иx(s+1) A . В силу x(s+1) = ϕ(x(s) )
x(s+1) − a = ϕ(x(s) )− a = ϕ(x(s) )− a + ϕ(a) − ϕ(a)= [ϕ(x(s) )− ϕ(a)]+ [ϕ(a)− a] ,
x(s+1) − a ≤ ϕ(x(s) )− ϕ(a) + ϕ(a) − a ≤ C x(s) − a + (1 − C)r ≤ Cr + (1 − C)r = r ,
то есть x(s+1) A . Далее оценивается разность получаемых решений для произвольной итерации с номером s:
x(s+1) − x(s) = ϕ(x(s) )− ϕ(x(s−1) ) ≤ C x(s) − x(s−1) .
Отсюда получается:
x(s+1) − x(s) ≤ C x(s) − x(s−1) ≤ C 2 x(s−1) − x(s−2) ≤…≤ C s x(1) − x(0) .
Для двух произвольных значений x( p) и x(q) (для определенности считает-
ся, что p > q) на основании этого соотношения получается:
x( p) − x(q) = (x( p) − x( p−1) )+ (x( p−1) − x(q) )=
= (x( p) − x( p−1) )+ (x( p−1) − x( p−2) )+ (x( p−2) − x(q) )=…= ∑p−1 (x(n+1) − x(n) ),
|
|
|
|
|
|
|
|
|
|
|
|
n=q |
|
||
|
|
p−1 |
|
|
|
|
|
p−1 |
p−q−1 |
||||||
x( p) − x(q) |
|
≤ ∑ |
|
x(s+1) − x(s) |
|
≤ |
|
x(1) − x(0) |
|
∑C s ≤ |
|
x(1) − x(0) |
|
C q |
∑C s = |
|
|
|
|
|
|
|
|||||||||
|
|
s=q |
|
|
|
|
|
|
|
s=q |
|
|
|
|
s=0 |
=x(1) − x(0) C q (1 + C + C 2 +…+ C p−q−1 )=
=x(1) − x(0) C q (1 − C p−q )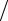 (1 − C)≤ x(1) − x(0) C q
(1 − C)≤ x(1) − x(0) C q 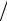 (1 − C).
(1 − C).
При выводе последнего соотношения использована формула для суммы членов геометрической прогрессии со знаменателем С, а также условие, что 0 < C <1, и тем более 0 < C p−q <1, p > q . При увеличении p и q имеет место
|
|
x( p) − x(q) →0 , |
|
|
|
|
|
|
|
|
p,q→∞ |
~ |
|
|
|
|
~ |
1 |
A, |
lim x |
(s) |
|||||
и в, соответствии с признаком Больцано–Коши |
, x |
|
|
= x . |
||||
|
|
|
|
|
s→∞ |
|
|
|
|
|
|
|
|||||
1 Больцано Бернард [5.10.1781 – 18.12.1848] – чешский математик, |
философ, теолог. |
|||||||
В 1800 году закончил философский, а в 1805 – теологический факультеты Пражского университета. В этом же университете с 1805 года возглавлял кафедру истории религии, откуда был уволен в 1820 году за вольнодумство и лишен права публичных выступлений. После этого занимался исследованием в области логики и математики.
75

При переходе к пределу в соотношении x(s) = ϕ(x(s−1) ) в силу непрерывно-
сти функции ϕ(x) получается: |
|
|
|
|
|
= limϕ(x |
|
|
|
)= ϕ(x ), |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x = lim x |
(s) |
(s−1) |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|||||||||||||
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
s→∞ |
|
|
|
|
|
|
s→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x является решением уравнения (3.2). Погрешность метода простой |
||||||||||||||||||||||||||||||||||||||||||||||
итерации после выполнения s итераций оценивается выражением |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
− x = ϕ(x |
|
|
|
|
|
)− ϕ(x ) ≤ C x |
|
|
|
|
|
− x ≤ C |
|
|
|
x |
|
− x ≤…, |
||||||||||||||||||||||||
|
|
|
(s) |
~ |
|
|
|
|
(s−1) |
|
|
|
|
~ |
|
|
|
|
|
(s−1) |
|
|
~ |
|
|
|
2 |
|
|
|
(s−2) |
~ |
|
|||||||||||||
откуда следует выражение (3.5) доказываемой теоремы: |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
− x ≤ C |
|
|
|
x |
|
|
|
− x . |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(s) |
|
|
|
|
~ |
|
|
s |
|
|
(0) |
|
~ |
|
|
|
|
|
|
|
|
|
|||||||
Осталось показать, что получаемое решение – единственно. В самом деле, |
||||||||||||||||||||||||||||||||||||||||||||||
~ |
~ |
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
пусть x |
= ϕ(x ) и x = ϕ(x ) – два различных решения уравнения (3.2). Тогда |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
~ |
|
|
|
~ |
|
= |
|
|
|
~ |
|
|
|
~ |
|
≤ C |
|
~ |
~ |
|
|
, |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
− x |
|
ϕ(x )− ϕ(x ) |
|
x |
− x |
|
|
|
|
|
||||||||||||||||||||||||||
что может иметь место при условии 0 < C < |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
~ |
||||||||||||||||||||||||||||||
1 лишь в случае x |
= x . Но это и оз- |
|||||||||||||||||||||||||||||||||||||||||||||
начает единственность получаемого решения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Что и требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Следствие. Если |
|
ϕ′x (x) |
|
≤ C <1 x A , а также выполнено соотношение |
||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ϕ(a)− a |
|
≤ (1 − C)r, |
|
|
x(0) A , |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
то уравнение (3.2) имеет единственное решение, метод простых итераций сходится и погрешность метода оценивается формулой (3.5).
Действительно, согласно теореме Лагранжа1,
Коши Огюстен Луи [21.8.1789 – 23.5.1857] – французский математик. В 1807 году окончил Политехническую школу, в 1810 году – Школу мостов и дорог в Париже. С 1810 по 1813 годы работал инженером в Шербурге. С 1816 года был избран членом Парижской академии наук. С 1816 по 1830 год преподавал в Политехнической школе и в Коллеж де Франс. С 1831 года стал иностранным почетным членом Петербургской академии наук. В 1848 году начал преподавать в Парижском университете.
Признак сходимости числовой последовательности Больцано–Коши [8]: для того, чтобы последовательность вещественных чисел имела конечный предел, необходимо и достаточно, чтобы x( p) − x(q) → 0 при p, q → ∞ .
1 Лагранж Жозеф Луи [25.11.1736 – 10.4.1813] – французский математик и механик. В 1755 году стал профессором Туринской артиллерийской школы. В 1759 году был избран членом Берлинской академии наук. С 1766 года был директором Математического класса Берлинской академии наук, с 1772 года – членом Парижской академии наук, с 1776 года – иностранным почетным членом Петербургской академии наук. В 1795 году стал профессором Парижской Нормальной школы, с 1797 года – профессором Политехнической школы.
76

ϕ(b) − ϕ(a) = ϕ′x (ξ)(b − a) = ϕ′x (ξ) b − a ≤ max ϕ′x (ξ) b − a ,
x A
то есть в качестве константы условия Липшица можно принять
C = max ϕ′x (x) .
x A
В этом случае условия рассматриваемой теоремы выполнены, и все ее утверждения имеют место.
Пример 3.2. Найти корень уравнения 2x + sin(x)=1. Уравнение преобразуется к стандартному виду
x= [1 − sin(x)] 2
2
ипредставляется в форме итерационного процесса:
x(S +1) = [1−sin(x(S ) )] 2 .
2 .
Таким образом, определен |
вид функции ϕ(x) = [1 − sin(x)] 2. |
Поскольку |
||||||
ϕ′x (x)= − cos(x) 2 , для проверки |
условий |
сходимости в качестве |
константы |
|||||
Липшица используется значение |
|
|
|
|
|
|
|
|
|
′ |
|
|
|
cos(x) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
C = max |
ϕx (x) |
= max |
|
|
|
= 0,5. |
|
|
|
|
|
||||||
x [0,1] |
|
|
x [0,1] |
2 |
|
|
|
|
Очевидно, что оба условия теоремы 3.1 выполняются, поскольку C <1 и
ϕ(a)− a = [1 − sin(0,5)]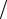 2 − 0,5 = 0,239713 < (1 − C)r = 0,25 ,
2 − 0,5 = 0,239713 < (1 − C)r = 0,25 ,
итерационный процесс сходится. Результаты расчетов даны в табл. 3.2. Таблица 3.2
Вычисление корня уравнения 2x + sin(x)=1 методом простых итераций с различными начальными значениями x(0)
Номер итерации |
Приближения решения |
|
|
|
|
|
|
0 |
x(0) = 0,0 |
|
x(0) = 1,0 |
1 |
0,5 |
|
0,0792645 |
|
|
|
|
2 |
0,2602872 |
|
0,4604092 |
|
|
|
|
3 |
0,3713209 |
|
0,2778426 |
|
|
|
|
Теорема Лагранжа [10]: если функция f(x) непрерывна в замкнутом интервале [a, b] и дифференцируема во всех его внутренних точках, то внутри этого интервала существует хотя бы одна точка ξ, для которой ( f (b) − f (a))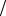 (b − a) = f x′(ξ) .
(b − a) = f x′(ξ) .
77

|
|
|
|
Окончание табл. 3.2. |
||
Номер итерации |
|
Приближения решения |
|
|||
|
|
|
|
|
|
|
4 |
|
0,3185767 |
|
|
0,3628592 |
|
|
|
|
|
|
|
|
5 |
|
0,3433924 |
|
|
0,3225257 |
|
6 |
|
0,3316583 |
|
|
0,3415185 |
|
|
|
|
|
|
|
|
7 |
|
0,3371943 |
|
|
0,3325409 |
|
|
|
|
|
|
|
|
8 |
|
0,3345797 |
|
|
0,3367771 |
|
|
|
|
|
|
|
|
9 |
|
0,3358139 |
|
|
0,3347765 |
|
|
|
|
|
|
|
|
10 |
|
0,3352311 |
|
|
0,3357210 |
|
|
|
|
|
|
|
|
… |
. . . . . . . . |
|
|
. . . . . . . |
||
|
|
|
|
|
|
|
30 |
|
0,3354180 |
|
|
0,3354180 |
|
|
|
|
|
|
|
|
3.3. Метод Ньютона1 |
|
|
~ |
|
||
Для поиска корней уравнения (3.1) в окрестности |
выбирается произ- |
|||||
x |
||||||
вольная точка x и функция f(x) раскладывается в ряд Тейлора2 возле x: |
||||||
~ |
~ |
|
|
|
||
|
f (x )= f |
(x)+ fx′(x)(x − x)+… |
|
|
||
Отсюда следует приближенное равенство |
|
|
||||
~ |
~ |
|
|
|
||
|
f (x )≈ |
f (x)+ fx′(x)(x − x), |
|
|
||
которое с учетом требования |
~ |
позволяет получить выражение |
f (x ) = 0 |
~ |
≈ x − f (x) fx′(x), |
x |
приводящее к итерационному процессу следующего вида:
x(s+1) = x(s) − f (x(s) ) fx′(x(s) ). |
(3.6) |
1Ньютон Исаак [4.1.1643 – 31.3.1727] – английский физик и математик. В 1655 году начал учебу в Грантемской школе, в 1661 году поступил в Тринити – колледж Кембриджского университета. В 1668 году ему была присвоена степень магистра. С 1669 по 1701 годы занимал почетную люкасовскую физико-математическую кафедру. С 1672 года был членом Лондонского королевского общества, президентом которого стал в 1703 году. В 1695 году получил должность смотрителя Монетного двора. В 1699 году был избран иностранным почетным членом Петербургской академии наук. В 1705 году за научные труды был возведен
вдворянское звание.
2Тейлор Брук [18.8.1685 – 29.12.1731] – английский математик. В 1712 году был избран членом Лондонского королевского общества.
78
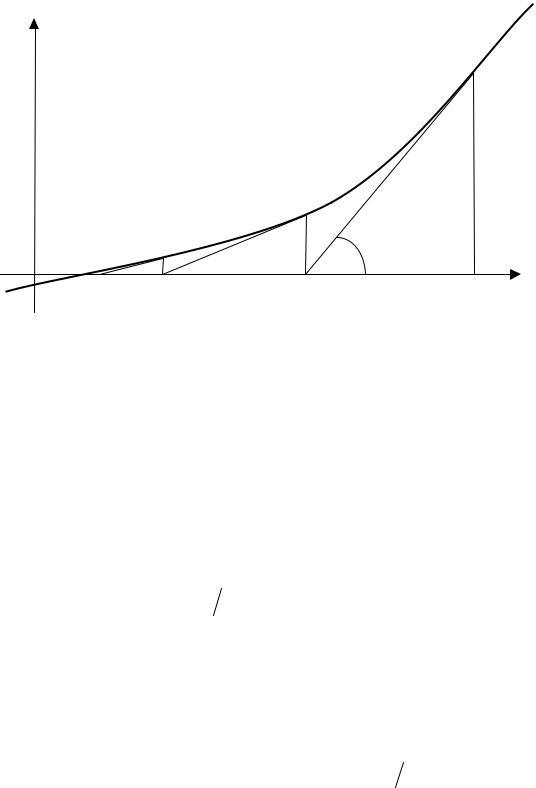
Очевидно, что метод Ньютона можно рассматривать как вариант метода простых итераций, если положить ϕ(x)= x − f (x) f ′(x). Геометрическая иллю-
f ′(x). Геометрическая иллю-
страция итерационного процесса метода Ньютона приведена на рис. 3.4.
f(x0)
|
|
f(x1) |
|
|
|
f(x2) |
|
α |
x |
|
|
|
|
|
x3 |
x2 |
x1 |
|
x0 |
Рис. 3.4. Геометрический смысл процедуры метода Ньютона
Из схемы понятно, что каждое следующее приближение может быть определено из геометрических построений:
x(s ) − x(s+1) = f (x(s) ) tg(α) = f (x(s) )
tg(α) = f (x(s) ) fx′(x(s) ).
fx′(x(s) ).
Теорема 3.2. Пусть выполнены следующие предположения:
–~ – корень уравнения f(x) = 0; x
– |
первая производная |
fx′(x)≠ 0 |
x A = {u |
|
~ |
|
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
| u − x |< r}; |
|
|
|
||||||||||||||||||||
– |
вторая производная |
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
fxx (x) непрерывна в А; |
|
′′ |
|||||||||||||||||||||
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|||
– |
константа C = M 2 |
x |
(0) |
− x |
|
|
2M1 <1, где M1 |
= inf |
fx (x) |
> 0, M 2 |
= sup |
fxx (x) |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x A |
|
|
x A |
|
|
Тогда если x(0) A , то метод Ньютона сходится, причем |
|
|
|
|||||||||||||||||||||
|
|
|
x |
(n) |
~ |
|
≤ C |
2n −1 |
|
x |
(0) |
~ |
|
. |
|
|
|
|
(3.7) |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
− x |
|
|
|
|
− x |
|
|
|
|
|
|||||||||
Доказательство. Для оценки погрешности решения используется формула Тейлора для разложения функции f(x) в ряд возле точки x(s) :
~ |
(x |
(s) |
)+ |
′ |
(x |
(s) |
~ |
− x |
(s) |
)+ |
′′ |
~ |
− x |
(s) |
2 |
ξ |
(s) |
(x |
(s) |
~ |
|
f (x )= f |
|
fx |
|
)(x |
|
fxx (ξ)(x |
|
) |
2, |
|
|
, x ). |
|||||||||
Поскольку |
~ |
– корень уравнения и |
|
~ |
|
|
|
|
|
|
|
|
|
||||||||
x |
f (x ) = 0, получается соотношение |
||||||||||||||||||||
79

|
|
|
− f (x |
|
|
|
) |
fx (x |
|
)= |
(x |
− x |
|
)+ |
|
fxx (ξ |
)(x − x |
|
|
) |
2 fx (x |
|
|
|
). |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(s) |
|
|
|
′ |
|
(s) |
|
|
~ |
|
|
|
(s) |
|
|
|
|
|
|
′′ |
|
|
(s) |
~ |
|
|
|
|
(s) |
2 |
|
|
′ |
|
(s) |
|
|
|
|
|
||||||
С другой стороны, согласно методу Ньютона, |
|
|
|
|
|
|
|
|
|
|
|
(x )= |
||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
− x = [x − f (x ) f |
(x )]− x = (x − x )− f (x ) f |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
(s+1) |
~ |
|
|
|
|
(s) |
|
|
|
|
(s) |
|
|
|
′ |
|
(s) |
|
|
|
|
~ |
|
|
(s) |
|
~ |
|
|
|
|
|
|
(s) |
|
|
′ |
|
|
|
(s) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
) |
|
|
|
|
|
). |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
= (x |
|
|
|
|
− x ) |
+ |
(x − x |
|
|
+ |
fxx |
(ξ |
|
|
)(x − x |
|
|
|
|
2 fx |
(x |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(s) |
|
~ ~ |
|
|
(s) |
|
|
|
′′ |
|
|
|
(s) |
|
~ |
|
(s) |
|
2 |
|
|
′ |
(s) |
|
|
|
|
|
|
|
|
|
|||||||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x |
(s+1) |
− |
~ = |
|
′′ |
ξ |
(s) |
|
~ |
− |
x |
(s) |
2 |
|
′ |
|
(s) |
|
|
|
|
|
|
|
|
|
|
|
|
(3.8) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
fxx |
( |
|
|
)(x |
|
|
|
|
) |
|
2 fx (x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
то есть имеет место квадратичная сходимость. Пусть |
|
x(0) A, |
|
|
ξ A, из фор- |
|||||||||||||||||||||||||||||||||||||||||||||||||
мулы (3.8) получается: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
(1) |
~ |
|
= |
|
′′ |
|
|
|
(0) |
)(x |
(0) |
|
~ |
2 |
|
|
|
′ |
|
(0) |
) |
|
≤ M 2 (x |
(0) |
|
|
~ |
2 |
2M1 = C |
|
x |
(0) |
~ |
|
, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
− x |
|
|
fxx (ξ |
|
|
|
|
− x ) |
|
2 fx (x |
|
|
|
|
− x ) |
|
|
|
− x |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то есть оценка (3.7) выполнена для s = 1. В предположении, что формула (3.7) верна для произвольного s, и с учетом условия С < 1, справедливо неравенство
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
− x ≤ C |
|
|
|
x |
|
|
|
− x ≤ x |
|
|
|
|
− x ≤ r , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(s) |
|
|
~ |
|
|
|
|
|
2s −1 |
|
|
(0) |
~ |
|
|
|
|
(0) |
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
то есть x(s) A, ξ(s) |
|
A , а следовательно, определены |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
= inf |
|
|
|
′ |
|
|
> 0, |
M 2 |
= sup |
|
′′ |
(x) |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fx (x) |
fxx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из соотношения (3.8) получается: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
x(s+1) − x |
|
≤ |
|
fxx′′ (ξ(s) )(x(s) − x)2 |
2 fx′(x(s) ) |
|
≤ M2 (x(s) − x)2 2M1 . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Согласно (3.7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(x |
(s) |
|
|
~ 2 |
|
|
|
x |
(s) |
|
~ |
|
|
x |
(s) |
~ |
|
≤ C |
2s −1 2s −1 |
(x |
(0) |
|
|
~ |
2 |
= C |
2s+1−2 |
(x |
(0) |
|
|
~ 2 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
− x ) = |
|
|
|
|
− x |
|
|
|
− x |
|
|
|
|
C |
|
|
|
|
|
|
|
− x ) |
|
|
|
|
|
|
|
|
− x ) . |
||||||||||||||||||||||||||||||||||||
С учетом этого из предыдущего выражения следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
(s+1) |
~ |
|
≤ M 2 |
(x |
(s) |
~ |
2 |
2M1 ≤ M 2C |
2s+1−2 |
(x |
(0) |
|
|
|
~ 2 |
2M1 |
= |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
− x |
|
|
|
− x ) |
|
|
|
|
|
|
|
|
|
− x ) |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
= C |
2s+1−2 |
(M 2 |
|
x |
(0) |
|
~ |
|
|
|
2M |
1 ) |
|
x |
(0) |
|
|
~ |
|
|
= C |
2s+1−2 |
C |
|
x |
(0) |
|
~ |
|
= C |
2s+1−1 |
|
x |
(0) |
~ |
|
. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− x |
|
|
|
|
|
|
− x |
|
|
|
|
|
|
|
|
|
|
− x |
|
|
|
|
|
|
|
− x |
|
||||||||||||||||||||||||||||||||
Но это как раз и означает, что формула (3.7) справедлива при s + 1. В силу C < 1 из выражения (3.7) следует сходимость метода Ньютона:
(s) − ~ → . x x s→∞ 0
Что и требовалось доказать.
Пример 3.3. Найти корень уравнения 2x + sin(x)−1 = 0.
80
