
Методы вычислительной математики
..pdf
которая теперь принимает значения t [−1,1]. В этом случае функция Pn (x) представляется в виде
|
2x − b − a |
|
Pn (x) = cos narccos |
|
. |
|
||
|
b − a |
|
Формула (2.6) преобразуется: |
|
|
Pn (x) = 2xPn−1 (x) − Pn−2 (x) = 2n−1[(2x − b − a)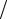 (b − a)]n +…= 22n−1 xn
(b − a)]n +…= 22n−1 xn 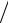 (b − a)n +…
(b − a)n +…
Теперь можно получить полином со старшим коэффициентом, равным 1, то есть полином Чебышёва, для отрезка [a, b]:
Tn (x) = |
(b − a)n |
|
2x − b − a |
(2.8) |
|
2 |
2n−1 |
cos narccos |
. |
||
|
|
b − a |
|
||
Корни этого многочлена определяются так же, как и ранее:
|
2x − b − a |
|
|
|
|||
cos narccos |
|
|
|
= 0 , |
|
|
|
|
|
||||||
|
|
b − a |
|
|
|
||
xk = b + a |
+ b − a cos |
(2k −1)π |
, k = |
|
. |
||
1,n |
|||||||
2 |
2 |
|
2n |
|
|
|
|
Очевидно, что в этом случае Tn = max[ ]Tn (x) = (b − a)n 22n−1 .
x a,b
Может также рассматриваться задача о построении многочлена степени n, наименее уклоняющегося от нуля на отрезке [a, b] среди многочленов, удовле-
творяющих условию Qn (0) =1. В этом случае полином (2.8) следует нормировать, чтобы Tn (0) =1,
T |
(x)= P (x) |
P (0)= p |
n |
cos narccos 2x − b − a |
, |
|||||||
n |
|
n |
|
n |
|
|
|
|
|
|||
где pn =1 cos(narccos((a + b) (a − b))). |
|
|
b − a |
|
||||||||
|
Корни этого многочлена расположены |
|||||||||||
в точках |
|
|
|
|
|
|
|
|
|
|
|
|
xk = |
b + a |
+ |
b − a |
cos((2k −1)π 2n), |
k = |
|
. |
|
||||
1,n |
|
|||||||||||
|
|
|
||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
||
Вводятся обозначения
ξ = a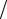 b, ρ0 = (1 − ξ)
b, ρ0 = (1 − ξ)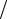 (1 + ξ)= (b − a)
(1 + ξ)= (b − a) (b + a).
(b + a).
Используя соотношения
y = arccos(z),
cos(y) = z – нечетная функция,
31

cos(2y) = 2cos2 (y)−1 = 2z2 −1 – четная функция,
cos(3y)= cos(y)[4cos2 (y) − 3] |
= 4z3 − 3z – нечетная функция, |
|
|
|||||||||||
cos(4y) = 2[2cos2 (y)−1]2 −1 = 2(2z2 −1)2 −1 – четная функция, |
|
|
||||||||||||
|
|
|
|
|
|
|
|
… |
|
|
|
|
||
cos(narccos(− z))= (−1)n cos(narccos(z)) = (−1)n (z + z2 |
−1)n + (z − z2 − |
1)n |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и полагая z = ρ0−1 , можно получить зависимости |
|
|
|
|||||||||||
z + z2 −1 =1 ρ0 + ρ0−2 −1 = (1 + ξ) (1 − ξ), |
|
|
||||||||||||
z − z2 −1 =1 ρ0 − ρ0−2 −1 = (1 − ξ) (1 + ξ). |
|
|
||||||||||||
С использованием обозначения ρ1 = (1 − |
ξ) (1 + |
ξ) определенный выше |
||||||||||||
коэффициент может быть представлен в виде |
|
|
|
|
||||||||||
|
|
|
|
|
pn = (−1)n 2ρ1n (1 + ρ12n ). |
|
|
|
||||||
Построенный полином принимает экстремальные значения, равные |
|
|
||||||||||||
|
T |
|
|
|
= max |
|
T (x) |
|
= 2ρn |
(1 + ρ2n ). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
n |
|
|
|
x [a,b] |
|
n |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.3. Прямые методы решения систем линейных алгебраических уравнений
Прямыми называют методы решения систем линейных алгебраических уравнений, для которых результат получается за конечное, заранее определенное, число арифметических операций. Наиболее известным среди них является метод Гаусса1.
2.3.1. Метод Гаусса
Процедура решения системы линейных алгебраических уравнений методом Гаусса рассматривается на примере:
2x1 + 4x2 − 6x3 = −8, |
||||||
|
|
|
|
|
|
|
|
1x1 |
+ 4x2 |
+1x3 =12, |
|||
|
||||||
|
2x |
+ 6x |
|
+ 0x |
|
=14. |
|
2 |
3 |
||||
|
1 |
|
|
|
||
1 Гаусс Карл Фридрих [30.4.1777 – 23.2.1855]. С 1795 по 1798 годы учился в Геттингенском университете. В 1799 году получил доцентуру в Брауншвейге, а с 1807 года – кафедру математики и астрономии Геттингенского университета, а также должность директора Геттингенской астрономической обсерватории. С 1802 года являлся иностранным (с 1824 – иностранным почетным) членом Петербургской академии наук.
32

Главный определитель этой системы
2 4 − 6 det(A)= 1 4 1 =8,
2 6 0
что гарантирует существование и единственность решения.
1 шаг. Первая строка системы уравнений делится на первый коэффициент
a11 = 2 :
|
1 |
+ 2x |
2 |
− 3x |
3 |
= −4, |
||
1x |
|
|
|
|
||||
|
1x1 |
+ 4x2 |
+1x3 |
=12, |
||||
|
||||||||
|
|
+ 6x |
|
+ 0x |
|
=14. |
||
2x |
2 |
|
||||||
|
1 |
|
|
|
|
3 |
||
2 шаг. Из второго уравнения вычитается первая строка, умноженная на коэффициент a21 =1:
1x1 + 2x2 − 3x3 = −4, |
||||||
|
|
|
|
|
|
|
|
|
+ 2x2 |
+ 4x3 |
=16, |
||
0x1 |
||||||
|
|
+ 6x |
|
+ 0x |
|
=14. |
2x |
2 |
3 |
||||
|
1 |
|
|
|
||
3 шаг. Из третьего уравнения вычитается первая строка, умноженная на коэффициент a31 = 2 :
1x1 + 2x2 − 3x3 = −4, |
||||||
|
|
|
|
|
|
|
|
|
+ 2x2 |
+ 4x3 =16, |
|||
0x1 |
||||||
|
|
+ 2x |
|
+ 6x |
|
= 22. |
0x |
2 |
3 |
||||
|
1 |
|
|
|
||
4 шаг. Второе уравнение делится на коэффициент a22 = 2 :
1x1 + 2x2 − 3x3 = −4, |
||||||
|
|
|
|
|
|
|
|
0x1 +1x2 |
+ 2x3 =8, |
||||
|
||||||
|
|
+ 2x |
|
+ 6x |
|
= 22. |
0x |
2 |
3 |
||||
|
1 |
|
|
|
||
5 шаг. Из третьего уравнения вычитается второе уравнение, умноженное на коэффициент a32 = 2:
|
1 |
|
2 |
|
− 3x |
3 |
= −4, |
|
1x + 2x |
|
|
|
|||||
|
0x1 |
+1x2 |
+ 2x3 =8, |
|||||
|
||||||||
|
0x |
+ 0x |
|
+ 2x |
|
= 6. |
||
|
2 |
3 |
||||||
|
1 |
|
|
|
|
|
||
6 шаг. Последовательно определяются искомые величины:
33

|
1 |
+ |
2x |
2 |
− 3x |
3 |
= −4, |
|
1 |
+ 2x |
2 |
− 3x |
3 |
= −4, |
1 |
= −4 − |
2x |
2 |
+ 3x |
3 |
=1, |
|||
1x |
|
|
1x |
|
|
|
x |
|
|
|||||||||||||||
|
0x1 +1x2 + 2x3 =8, |
|
x2 =8 − 2x3 = 2, |
|
x2 = 2, |
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
x |
|
= |
6 2 = 3; |
|
|
x |
|
= 3; |
|
|
|
x |
|
= 3. |
|
|
||||||
|
|
3 |
|
|
3 |
|
|
|
3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Теперь процедура получения решения методом Гаусса рассматривается в общем случае. Предполагается, что a11 ≠ 0, тогда первое уравнение системы
(2.2) можно поделить на этот коэффициент:
1x1 + c12 x2 + c13 x3 +…+ c1m xm = y1 = f1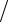 a11 .
a11 .
С помощью этого уравнения система (2.2) преобразуется к виду
1x1 + c12 x2 + c13 x3 +…+ c1m xm = y1 , |
|
|
|
|||||||
|
+ a |
(1) |
x2 |
(1) |
x3 |
(1) |
= f |
(1) |
= f2 |
− a21 y1 , |
0x1 |
22 |
+ a23 |
+…+ a2m xm |
2 |
||||||
|
+ a |
(1) |
x2 |
(1) |
x3 |
(1) |
= f |
(1) |
= f3 |
− a31 y1 , |
0x1 |
32 |
+ a33 |
+…+ a3m xm |
3 |
||||||
……………………………………………………… |
||||||||||
|
+ am(1)2 x2 |
+ am(1)3 x3 |
+…+ amm(1) xm = fm(1) |
= fm − am1 y1 , |
||||||
0x1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
где обозначено: ai(1j) = ai j − ai1c1 j , i, j = 2, m . В полученной системе можно вы-
делить подсистему m – 1 уравнения с m – 1 неизвестной величиной:
a |
2(12) x2 |
+ a2(13) x3 |
+…+ a2(1m) xm = f2(1) |
, |
||
|
|
(1) |
(1) |
(1) |
(1) |
, |
a |
32 x2 |
+ a33 x3 |
+…+ a3m xm |
= f3 |
||
|
………………………………… |
|||||
|
||||||
|
|
(1) |
(1) |
(1) |
(1) |
|
am2 x2 |
+ am3 x3 |
+…+ amm xm |
= fm . |
|||
В предположении, что коэффициент a2(12) ≠ 0 , второе уравнение системы
можно поделить на него:
0x1 +1x2 + c23 x3 +…+ c2m xm = f2(1) 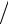 a2(12) = (f2 − a21 y1 )
a2(12) = (f2 − a21 y1 )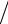 a2(12) = y2 .
a2(12) = y2 .
Это соотношение позволяет преобразовать остальные уравнения к виду
1x1 + c12 x2 + c13 x3 |
+…+ c1m xm = y1 , |
|
|
|
||||
0x1 +1x2 + c23 x3 +…+ c2m xm = y2 , |
(1) |
(1) |
|
|||||
|
+ 0x2 |
(2) |
x3 |
( 2) |
( 2) |
, |
||
0x1 |
+ a33 |
+…+ a3m xm = |
f3 |
= f3 |
− a32 y2 |
|||
……………………………………………………… |
|
|||||||
|
+ 0x2 |
+ am(23) x3 |
+…+ amm( 2) xm = fm( 2) = fm(1) |
− am(12) y2 , |
||||
0x1 |
||||||||
|
|
|
|
|
|
|
|
|
34

где ai(2j ) = ai(1j) − ai(21)c2 j , i, j = 3,m . В результате преобразований получена под-
система m – 2 уравнений с m – 2 неизвестными:
a3(32) x3 |
+…+ a3(m2) xm = f3( 2) , |
|||
|
………………………… |
|
||
|
|
|||
|
( 2) |
( 2) |
( 2) |
. |
am3 x3 |
+…+ amm xm |
= fm |
||
Если a3(32) ≠ 0 , третье уравнение системы можно поделить на него:
0x1 + 0x2 +1x3 +…+ c3m xm = f3(2)  a33(2) = (f3 − a31 y1 − a32(1) y2 )
a33(2) = (f3 − a31 y1 − a32(1) y2 )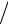 a33(2) = y3 .
a33(2) = y3 .
Далее выполняется очередной шаг по понижению порядка системы алгебраических уравнений, и так до тех пор, пока вся система уравнений не будет преобразована к виду
1x1 + c12 x2 + c13 x3 + …+ c1m xm = y1 , |
||||
|
1x2 + c23 x3 + …+ c2m xm = y2 , |
|||
|
1x3 + …+ c3m xm = y3 , |
|||
|
||||
|
…………………… |
|||
|
||||
|
1x |
m |
= y |
. |
|
|
m |
|
|
В результате выполнения всех операций матрица коэффициентов А системы алгебраических уравнений приводится к виду
1 c12 |
c13 |
… c1m |
|
|
|
|
|
|
|
|
|
0 |
1 |
c23 |
… c2m |
|
|
|
|
|
|
|
, |
U = 0 0 |
1 |
… c3m |
|
||
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
0 |
0 |
… 1 |
|
|
0 |
|
|
|||
соответствующему верхней треугольной матрице1, у которой на главной диагонали расположены единицы и равны нулю все элементы под главной диагональю. Процедура получения такой матрицы носит название «прямого хода» метода Гаусса. Очевидно, что для успешного выполнения «прямого хода» является условие
1 Обозначение U принято по первой букве английского слова upper – «верхняя».
35

a(j jj−1) ≠ 0, j =1,m .
«Обратный ход» метода Гаусса позволяет найти искомые величины:
xm = ym , |
|
|
|
|
|
|
|
|
|
||||
|
|
|
= ym−1 − cm−1m xm , |
|
|
|
|
|
|||||
xm−1 |
|
|
|
|
|
||||||||
|
|
|
= y |
|
− c |
|
x |
|
− c |
|
x |
|
, |
x |
m−2 |
m−1 |
m−2m |
m |
m−2m−1 |
m−1 |
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= y1 − ∑c1 j x j . |
|
|
|
|
|
|
|
|||||
x1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
j=2 |
|
|
|
|
|
|
|
|
|
«Прямой ход» метода Гаусса можно трактовать как преобразование системы уравнений вида Ax = f в эквивалентную систему Ux = y, причем
y1 = f1 a11 , y2 = f2(1)
a11 , y2 = f2(1)  a2(12) = ( f2 − a21 y1 )
a2(12) = ( f2 − a21 y1 ) a22(1) , …
a22(1) , …
Последнюю систему соотношений с учетом вышеприведенных выкладок можно представить в иной форме –
f1 = a11 y1 |
|
|
|
|
|
|
|
|
|
|
||
f |
2 |
= a y |
+ a(1) y |
2 |
|
|
|
|
|
|
||
|
21 1 |
|
22 |
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
2 |
) y3 |
|
|
|
f3 |
= a31 y1 + a32( ) y2 |
+ a33( |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ a(1) |
|
|
|
+ a(2) y |
+…a(m−1) y |
|
|
|
f |
m |
= a y |
|
y |
2 |
m |
, |
|||||
|
m1 1 |
m2 |
|
|
m3 3 |
mm |
|
|||||
и записать в виде Ly = f , где
a11a21 L = a31
am1
0
a22(1) a32(1)
am(12)
0 |
… |
0 |
|
0 |
… |
0 |
|
|
|||
(2) |
|
|
|
|
|
|
|
a33 |
… |
0 |
|
|
… |
|
|
(2) |
|
|
|
… |
(m−1) |
||
am3 |
amm |
|
|
– нижняя |
треугольная матрица1 с отличными от нуля коэффициентами |
||
a(j jj−1) ≠ 0, |
j = |
|
на главной диагонали. Все вышесказанное позволяет тракто- |
1,m |
|||
1 Обозначение L принято по первой букве английского слова lower – «нижний».
36
вать метод Гаусса как последовательное решение двух систем уравнений – Ly = f и Ux = y. Объединение этих соотношений приводит к выражению
LUx = f .
Сравнивая последнее соотношение с формулой (2.1), можно сделать заключение, что процедура метода Гаусса эквивалентна разложению исходной матрицы коэффициентов А в произведение двух матриц A = LU, где L – нижняя треугольная матрица с ненулевыми коэффициентами на главной диагонали, U – верхняя треугольная матрица с единицами на главной диагонали.
Для угловых миноров матрицы А вводятся обозначения:
|
= a , |
|
= |
|
a11 |
a12 |
|
|
= |
a11 |
a12 |
a13 |
|
|
= det(A). |
|||
|
|
|
|
|
|
|
||||||||||||
1 |
2 |
|
, |
3 |
a |
a |
22 |
a |
23 |
, …, |
m |
|||||||
11 |
|
|
|
a21 |
a22 |
|
|
21 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
a31 |
a32 |
a33 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Теорема 2.2. Если все угловые миноры квадратной матрицы А отличны от |
||||||||||||||||||
нуля, j ≠ 0, j = |
|
, то А можно представить единственным образом в виде |
||||||||||||||||
1,m |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
A = LU, |
|
|
|
|
|
|
(2.9) |
||
где L – нижняя треугольная матрица с ненулевыми диагональными элементами, U – верхняя треугольная матрица с единицами на главной диагонали.
Доказательство теоремы проводится по индукции. Рассматривается разложение матрицы А для простейшего случая m = 2. В этом случае матрицы A, L
и U имеют вид |
|
|
|
|
λ11 |
|
|
|
|
|
|
|
|
A2 |
a11 |
a12 |
|
L2 |
|
0 |
|
1 u12 |
|
|
|
||
= |
a22 |
, |
= |
λ22 |
, U2 |
= |
. |
|
|||||
|
a21 |
|
|
λ21 |
|
|
0 1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предполагая разложимость для m = 2, |
|
|
|
|
|
|
|
|
|||||
A2 = L2U2 |
λ11 |
0 1 u12 |
|
= |
λ11 |
|
λ11u12 |
|
|
, |
|||
= |
|
λ22 |
|
|
|
λ21u12 + λ22 |
|
||||||
|
|
λ21 |
0 1 |
|
|
λ21 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можно получить систему линейных алгебраических уравнений относительно коэффициентов матриц L2 и U2:
λ11 = a11; λ11u12 = a12 ; λ21 = a21; λ21u12 + λ22 = a22 .
Решение этой системы позволяет вычислить искомые коэффициенты
λ11 = a11 = 1 ≠ 0; λ21 = a21 ; u12 = a12  a11 ;
a11 ;
λ22 = a22 − a21a12  a11 = (a11a22 − a21a12 )
a11 = (a11a22 − a21a12 ) a11 = 2
a11 = 2  1 ≠ 0 .
1 ≠ 0 .
37
Это означает, что возможность разложения (2.9), соответствующего условию теоремы, показана для простейшего случая m = 2. Далее предполагается, что условия теоремы выполнены для случая m – 1, то есть имеет место разложение Am−1 = Lm−1Um−1 .
Вводятся обозначения
am−1 = am 1 |
am 2 |
… am m−1 , |
|
|
λm−1 = λm1 |
λm2 |
… λmm−1 , |
||||||||
{am−1} = a1m |
a2m2 |
… am −1m |
T , |
|
{um−1} = u1m u2m … um−1 m |
T , |
|||||||||
|
0 = 0 0 … 0 , |
|
{0} = 0 0 … 0 T , |
|
|
|
|||||||||
позволяющие представить матрицы Am , |
Lm , Um в форме |
|
|
|
|
||||||||||
|
Am−1 |
{am−1} |
Lm−1 |
{0} |
|
Um−1 |
{um−1} |
|
|||||||
Am = |
a |
a |
, |
Lm = |
λ |
m−1 |
λ |
m m |
, Um = |
0 |
1 |
. |
|||
|
m−1 |
m m |
|
|
|
|
|
|
|
|
|
|
|||
Используя введенные обозначения, можно показать существование разложения для матрицы Am: перемножение LmUm и сравнение полученного результата со структурой матрицы Am дает систему 2m – 1 алгебраического уравнения относительно 2m – 1 неизвестных величин {um−1},  λm−1
λm−1  и λmm :
и λmm :
L |
{u |
m−1 |
}={a |
m−1 |
}, |
||
|
m−1 |
|
|
|
|
||
|
λm−1 |
Um−1 = am−1 , |
|||||
|
|||||||
|
λm−1 |
{um−1}+ λmm = amm. |
|||||
|
|||||||
|
|
|
|
|
|
|
|
В силу того, что det(Lm−1 ) ≠ 0, det(Um−1 ) ≠ 0 (треугольные матрицы с ненулевыми значениями на главных диагоналях), существуют единственные решения первых двух систем уравнений: {um−1}= L−m1−1{am−1},  λm−1
λm−1  =
=  am−1
am−1  Um−1−1 . Также может быть вычислено последнее неизвестное λmm = amm −
Um−1−1 . Также может быть вычислено последнее неизвестное λmm = amm − 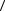 λm−1
λm−1 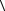 {um−1}, значение которого должно быть отлично от нуля. С учетом того, что
{um−1}, значение которого должно быть отлично от нуля. С учетом того, что
det(A) = det(Am ) = det(LmUm ) = det(Lm )det(Um ) = λmm det(Lm−1 )det(Um−1 ) , det(A) ≠ 0, det(Lm−1 ) ≠ 0, det(Um−1 ) =1,
имеет место равенство det(A) = λmm det(Lm−1 ) , из которого следует, что λmm ≠ 0. При выполнении преобразований учтено, что матрицы Lm,Um являются диаго-
38
нальными, а их определители представлены разложениями соответственно по последнему столбцу и нижней строке.
Доказательство единственности разложения (2.9) ведется «от противного». Предполагается, что искомое разложение не единственно, то есть
A = L(1)U(1) = L(2)U(2) .
С помощью простейших преобразований получается
L(1) = L(2)U(2)U(−11) ,
L−(21) L(1) = U(2)U(−11) .
Поскольку исходные и обратные матрицы сохраняют свою «треугольную» форму, в левой части последнего выражения расположена нижняя треугольная матрица, а в правой части – верхняя треугольная. Но равенство в этом случае
возможно лишь тогда, когда матрицы |
L−1 |
L |
и U |
|
U −1 |
являются диагональ- |
|||||||||||
|
|
|
|
|
|
(2) |
(1) |
|
|
(2) |
|
(1) |
|
|
|
|
|
ными. Более того, поскольку U(2) |
и U(−11) содержат единицы на главной диаго- |
||||||||||||||||
нали, |
полученные диагональные матрицы |
|
будут |
|
единичными, то есть |
||||||||||||
L−1 |
L |
= U |
U −1 = E . А отсюда следует, что L |
|
= L |
|
, |
U |
(1) |
= U |
(2) |
, но это и оз- |
|||||
(2) |
(1) |
|
(2) (1) |
|
|
|
(1) |
|
(2) |
|
|
|
|
||||
начает единственность разложения (2.9). |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
В качестве примера рассматривается матрица коэффициентов системы ли- |
||||||||||||||||
нейных алгебраических уравнений следующего вида: |
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = 1 |
1 , det(A) = −1 ≠ 0 . |
|
|
|
|
|
||||||||
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первый шаг метода Гаусса приводит матрицу к виду |
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = 0 |
0 |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нулевое значение на главной диагонали матрицы вызывает аварийную остановку вычислительного процесса, поскольку для исходной матрицы А один
из угловых миноров равен нулю: 2 |
= |
1 |
1 |
= 0 , то есть имеется противоречие |
|
|
1 |
1 |
|
условиям теоремы 2.2. Для успешного выполнения процедуры метода Гаусса
39
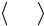
следует поменять местами строки |
матрицы А (смена столбцов приведет |
|||
к необходимости изменить порядок неизвестных), например, |
||||
|
|
1 |
1 |
0 |
* |
= |
|
1 |
|
A |
0 |
1 . |
||
|
|
1 |
1 |
1 |
|
|
|
|
|
Приведение исходной матрицы к новому виду можно интерпретировать как преобразование вида A* = PA . Для рассматриваемого случая преобразование Р имеет вид
|
0 |
0 |
|
1 |
|
||
|
0 |
|
|
P = 0 |
1 . |
||
|
1 |
|
|
0 |
0 |
||
|
|
|
|
Теорема 2.3. Если определитель матрицы коэффициентов det(A) ≠ 0 , то существует матрица перестановок Р такая, что у матрицы A* = PA все угловые миноры отличны от нуля.
Доказательство теоремы проводится по индукции. Рассматривается простейший случай – матрица коэффициентов системы двух уравнений:
|
|
a11 |
a1 2 |
|
|
||
|
|
A2 = a |
21 |
a |
. |
|
|
|
|
|
|
2 2 |
|
|
|
Если a11 |
≠ 0, теорема 2.3 справедлива при Р = Е, то есть в случае тождест- |
||||||
венного преобразования. |
|
|
|
|
|
= −a12 a21 ≠ 0 , то |
|
Предполагается, что a11 = 0 . Так как det(A) = a11a22 − a12 a21 |
|||||||
a21 ≠ 0, и исходная матрица может быть преобразована к виду |
|
||||||
|
* |
a21 |
a2 2 |
|
0 1 |
|
|
|
A2 |
= PA2 = |
a1 2 |
|
, P = |
. |
|
|
|
a11 |
|
1 0 |
|
||
Теперь |
1 = a21 ≠ 0, |
2 = a21a12 − a11a22 |
≠ 0 , то есть при m = 2 теорема 2.3 |
||||
справедлива. Пусть утверждение теоремы также верно и для |
Аm−1 . Рассматри- |
||||||
вается матрица Am (обозначения введены ранее):
|
Am−1 |
{am−1} |
|
Am = |
a |
a |
. |
|
m−1 |
m m |
|
40
