
Методы вычислительной математики
..pdf1.3.Укажите источники погрешностей математической модели. Какие из погрешностей являются неустранимыми, а какие – регулируемыми?
1.4.Объясните причины возникновения погрешностей исходных данных.
1.5.Что понимается под погрешностью численного метода?
1.6.Как оценить величину погрешности вычислений на ЭВМ?
1.7.Какую погрешность: относительную или абсолютную – целесообразно оценивать при выполнении вычислений на ЭВМ и почему?
21

2. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Система m линейных алгебраических уравнений с m неизвестными величинами представляется в виде
Ax = f , |
|
|
(2.1) |
|
где A – квадратная матрица ранга m; |
f = f1 |
f2 |
f3 … fm |
T – правая часть |
системы уравнений; x = x1 x2 x3 |
… xm |
T |
– искомый |
вектор. Система |
уравнений (2.1) имеет единственное решение, если определитель матрицы A отличен от нуля, det(A)≠ 0 . В развернутой (компонентной) записи эта система уравнений имеет вид
a11x1 + a1 2 x2 + a1 3 x3 +…+ a1 m xm = f1, |
|
a21x1 + a2 2 x2 + a2 3 x3 +…+ a2 m xm = f2 , |
|
|
(2.2) |
a31x1 + a3 2 x2 + a3 3 x3 +…+ a3 m xm = f3 , |
|
………………………………………… |
|
|
|
am 1x1 + am 2 x2 + am 3 x3 +…+ am m xm = fm. |
|
2.1. Устойчивость системы линейных алгебраических уравнений
Для оценки влияния изменения (возмущения) правой части f и матрицы коэффициентов А на решение x системы линейных алгебраических уравнений (2.1) вводится линейное пространство Rm векторов размерности m, в котором определяется норма, удовлетворяющая условиям [8]:

 x
x
 ≥ 0 x Rm , x ≠ 0 ;
≥ 0 x Rm , x ≠ 0 ;

 x
x
 = 0 x = 0 ;
= 0 x = 0 ;

 αx
αx
 = α
= α

 x
x
 ;
;

 x + y
x + y
 ≤
≤ 
 x
x
 +
+ 
 y
y
 .
.
В пространстве Rm в качестве нормы вектора могут быть взяты определения «кубической» нормы
x = max xi
1≤i≤m
или «сферической» нормы [40]
m

 x = ∑xi2 .
x = ∑xi2 .
i=1
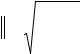
Норма матрицы (оператора) определяется согласно [8] выражением
22
|
|
|
|
|
|
A |
|
|
|
|
|
= sup |
|
|
|
|
|
|
|
|
|
|
Ax |
|
|
|
= sup |
|
|
|
Ax |
|
|
|
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x Rm , x≠0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
≤1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Из последнего определения, в частности, следуют известные соотношения |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
для норм матриц и векторов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ax |
|
|
|
≤ |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
A + B |
|
|
|
≤ |
|
|
|
|
A |
|
|
|
+ |
|
|
|
B |
|
|
|
, |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
AB |
|
|
|
≤ |
|
|
|
A |
|
|
|
|
|
|
|
|
B |
|
|
|
, |
|
|
|
|
|
E |
|
|
|
|
|
=1, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
где Е – тождественный оператор, ei j = δi j , |
i, j = |
|
. В качестве нормы матрицы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1,m |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
А может быть взято определение [8] «сферической» нормы |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
|
|
∑aij2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i, j=1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
либо определение [40] «кубической» нормы |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
= max ∑ |
|
ai j |
|
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1≤i≤m |
j=1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
~ |
– «возмущенная» правая часть системы уравнений (2.1). Необхо- |
|||||||||||||||||||||
Пусть f |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
димо оценить изменение решения δx = x − x как результат изменения правой |
|||||||||||||||||||||||
части |
δf = f |
− f . |
|
||||||||||||||||||||
Система уравнений Ax = f |
называется устойчивой по правой части, если |
||||||||||||||||||||||
~ |
|
δx |
|
≤ M |
|
δf |
|
, где M > 0 |
– положительная константа. Это, в частности, |
||||||||||||||
|
|
|
|
||||||||||||||||||||
f , f |
|
|
|
|
|||||||||||||||||||
означает, что |
|
δx |
|
|
|
→ 0 при |
|
|
|
δf |
|
|
|
|
→ 0 , то есть имеется непрерывная зависимость |
||||||||
|
|
|
|
|
|
|
|||||||||||||||||
решения от правой части.
Пусть определитель матрицы А отличен от нуля. В этом случае существует обратная матрица A−1 . Используя свойство линейности системы алгебраических уравнений, можно получить оценку возмущения 
 δx
δx
 :
:
Aδx = A(x − x) = Ax − Ax = f − f = δf ,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δx = A−1δf , |
|
||||||||||||||||
то есть |
|
|
|
δx |
|
|
|
= |
|
|
|
A−1δf |
|
|
|
≤ |
|
|
|
A−1 |
|
|
|
|
|
|
|
δf |
|
|
|
, откуда вытекает, что |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δx |
|
|
|
≤ |
|
|
|
A−1 |
|
|
|
|
|
|
|
δf |
|
|
|
|
(2.3) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23

и роль константы М может выполнять норма обратной матрицы 
 A−1
A−1 
 . Чем ближе значение det(A) к нулю, тем больше величина
. Чем ближе значение det(A) к нулю, тем больше величина 
 A−1
A−1 
 и тем значительнее
и тем значительнее
отклонение δx при заданном возмущении δf. Из уравнения (2.1) следует:

 f
f 
 =
= 
 Ax
Ax
 ≤
≤ 
 A
A


 x
x
 .
.
Перемножение двух последних неравенства дает оценку

 δx
δx


 f
f 
 ≤
≤ 
 A−1
A−1 


 δf
δf 


 A
A


 x
x
 ,
,

 δx x ≤
δx x ≤ 
 A−1
A−1 


 A
A


 δf
δf 

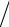

 f
f 
 = M A δf f ,
= M A δf f ,
где произведение M A = 
 A−1
A−1 


 A
A
 называется числом обусловленности матри-
называется числом обусловленности матри-
цы А, характеризующим зависимость относительной погрешности 
 δx
δx

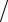

 x
x
 решения системы уравнений от относительного «возмущения»
решения системы уравнений от относительного «возмущения» 
 δf
δf 

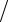

 f
f 
 правой части. Очевидно, что при подходящем выборе нормы
правой части. Очевидно, что при подходящем выборе нормы
1 = 
 E
E
 =
= 
 A−1 A
A−1 A
 ≤
≤ 
 A−1
A−1 


 A
A
 = M A .
= M A .
Пример 2.1. Для системы линейных алгебраических уравнений
0,780x + 0,563y = 0,217,0,913x + 0,659 y = 0,254,
оценить устойчивость решения по отношению к возмущению «правой» части. Определитель этой системы линейных алгебраических уравнений
det(A)= 0,780 0,659 − 0,563 0,913 =10−6
отличен от 0, хотя и мал. Матрица коэффициентов представляется в виде
0,780 |
0,563 |
A = |
. |
0,913 |
0,659 |
|
|
Вычисление обратной матрицы приводит к значениям коэффициентов
659000 |
− 563000 |
A−1 = |
. |
− 913000 |
780000 |
|
|
Определитель обратной матрицы равен
= 659000 780000 − 563000 913000 =106 .
24
При использовании определения «сферической» нормы матрицы для рассматриваемого случая получаются значения

 A
A
 =1,48095,
=1,48095, 
 A−1
A−1 
 =1480950.
=1480950.
Это позволяет оценить число обусловленности заданной матрицы А, то есть показатель устойчивости решения при возмущении правой части системы уравнений M A = 2193219 , которое значительно больше 1, поэтому заданную
систему уравнений следует признать неустойчивой по отношению к возмущению «правой» части.
В более общем случае рассматривается одновременное возмущение и правой части δf, и матрицы коэффициентов δA системы линейных алгебраических
уравнений: |
~ |
~ |
~~ |
||
Ax |
= f , |
A = A + δA . |
Для получения оценки устойчивости решения системы алгебраических уравнений в общем случае необходимо рассмотреть вспомогательное утверждение.
Лемма 2.1. Пусть С – квадратная матрица, 
 C
C
 <1; Е – единичная матрица. Тогда существует (E + C)−1 , причем
<1; Е – единичная матрица. Тогда существует (E + C)−1 , причем

 (E + C)−1
(E + C)−1 
 ≤ (1 −
≤ (1 − 
 C
C
 )−1 .
)−1 .
Доказательство. Для любого x имеет место неравенство
|
(E |
+ C)x |
|
|
|
= |
|
|
|
x + Cx |
|
|
|
≥ |
|
|
|
x |
|
|
|
|
− |
|
|
|
Cx |
|
|
|
≥ |
|
|
|
|
|
|
x |
|
|
|
− |
|
|
|
|
|
C |
|
|
|
|
|
|
|
x |
|
|
|
= (1 − |
|
|
|
C |
|
|
|
) |
|
|
|
x |
|
|
|
= δ |
|
|
|
x |
|
|
|
, |
(2.4) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
где δ =1 |
− |
|
|
|
C |
|
|
|
> 0 по условию леммы. Рассматривается однородное уравнение |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(E + C)x = 0 |
|
|
|
. Из неравенства (2.4) следует: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(E + C)x |
|
|
|
= |
|
|
|
|
|
0 |
|
≥ δ |
|
|
|
x |
|
|
|
, |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
что возможно лишь при 
 x
x
 = 0, откуда следует, что x = 0. Иными словами, однородное уравнение (E + C)x = 0 имеет только тривиальное решение. Но это означает, что определитель det(E + C) не равен нулю, то есть существует обратная матрица (E + C)−1 . Далее рассматривается уравнение
= 0, откуда следует, что x = 0. Иными словами, однородное уравнение (E + C)x = 0 имеет только тривиальное решение. Но это означает, что определитель det(E + C) не равен нулю, то есть существует обратная матрица (E + C)−1 . Далее рассматривается уравнение
(E + C)x = y ,
имеющее решением x = (E + C)−1 y . С помощью выражения (2.4) получается

 (E + C)x
(E + C)x
 ≥ δ
≥ δ
 x
x
 = δ
= δ
 (E + C)−1 y
(E + C)−1 y
 ,
,
25


 (E + C)−1 y
(E + C)−1 y
 ≤ (E + C)x δ = y δ = y
≤ (E + C)x δ = y δ = y 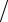 (1 − C ).
(1 − C ).
Полученное неравенство используется для подсчета нормы.
|
(E + C)−1 |
|
= sup |
|
(E + C)−1 y |
|
|
|
≤ sup |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
= sup |
1 |
|
|
|
= (1 − |
|
C |
|
)−1 |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
y |
|
|
|
|
(1 − |
|
|
|
|
C |
|
|
|
) |
|
y |
|
(1 − |
|
C |
|
) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
y |
|
≠0 |
|
|
|
|
|
y |
|
≠0 |
|
|
|
|
|
|
|
|
|
y |
|
≠0 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что и требовалось доказать.
Теорема 2.1. Пусть матрица А имеет обратную и выполнено условие
|
δA < A−1 −1 . |
Тогда матрица |
~ |
A = A + δA обратима и справедлива оценка погрешности |

 δx
δx

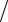

 x
x
 ≤ M A (
≤ M A (
 δA
δA

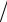

 A
A
 +
+ 
 δf
δf 



 f
f 
 )
)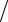 (1 − M A
(1 − M A 
 δA
δA



 A
A
 ).
).
Доказательство. Согласно определению
~ |
−1 |
δA)= A(E + C), |
C = A |
−1 |
δA. |
A = A + δA = A(E + A |
|
|
С использованием условия теоремы оценивается норма матрицы С:

 C
C
 =
= 
 A−1δA
A−1δA
 ≤
≤ 
 A−1
A−1 


 δA
δA
 <
< 
 A−1
A−1 

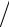

 A−1
A−1 
 =1.
=1.
В силу того что матрица С удовлетворяет условию леммы 2.1, существует матрица (E + C)−1 . Поскольку
~−1 = [ ( + )]−1 = ( + )−1 −1
A A E C E C A
,
|
|
~ |
−1 |
существует в силу существования матриц A |
−1 |
|
и |
(E + C) |
−1 |
. От- |
||||||||||||||||||||||||||||||||||||||||||||
то матрица A |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
клонение возмущенного решения от исходного определяется формулой |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
~ |
|
~ |
−1 |
~ |
|
|
−1 |
|
|
|
~−1 ~ |
|
~−1 |
|
|
|
|
~−1 |
f |
− A |
−1 |
~ |
−1 |
|
~ |
|
|
|
|
|
~−1 |
− A |
−1 |
)f . |
||||||||||||||||||||
δx = x − x = A f − A |
|
f = A f − |
A |
f + A |
|
|
|
f = A |
|
|
(f |
− f )+ |
(A |
|
|
|||||||||||||||||||||||||||||||||||||||
С учетом того, что |
~ |
− f = δf , |
|
f = Ax , получается: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
~ |
−1 |
δf |
|
|
|
~−1 |
− |
A |
−1 |
)Ax = |
~ |
−1 |
δf |
|
|
|
|
~−1 |
A − A |
−1 |
A)x = |
~ |
−1 |
δf |
~ |
−1 |
A − E)x |
, |
||||||||||||||||||||||||||
δx = A |
|
+ (A |
|
|
A |
|
+ (A |
|
|
A |
|
+ (A |
||||||||||||||||||||||||||||||||||||||||||
откуда следует оценка |
|
|
|
|
A − E)x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
δx |
|
= |
|
~−1 |
δf |
~−1 |
|
|
|
≤ |
|
|
|
~−1 |
|
|
δf |
|
+ |
|
|
|
~−1 |
A − E |
|
x |
|
. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
A |
|
+ (A |
|
|
|
|
|
|
A |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Слагаемые в правой части этого неравенства оцениваются раздельно:
|
|
A~−1 |
|
= |
|
(E + C)−1 A−1 |
|
≤ |
|
(E + C)−1 |
|
|
|
A−1 |
|
≤ |
|
A−1 |
|
(1 − |
|
|
|
C |
|
|
|
)≤ A−1 |
(1 − A−1 δA ); |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
~ |
−1 |
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
−1 |
|
|
|
−1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
A − E |
= |
|
|
A − E |
= |
[A(E + A |
δA)] A − E |
|
= |
|
A − E |
= |
||||||||||||||||||||||||||||
|
A |
|
(A + δA) |
|
|
|
|
[A(E + C)] |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26

= 
 (E + C)−1 A−1 A − E
(E + C)−1 A−1 A − E
 =
= 
 (E + C)−1 − E
(E + C)−1 − E
 =
= 
 (E + C)−1[E − (E + C)]
(E + C)−1[E − (E + C)]
 =
= 
 − (E + C)−1C
− (E + C)−1C
 ≤
≤
≤ 
 (E + C)−1
(E + C)−1 


 C
C
 ≤
≤ 
 C
C
 (1 −
(1 − 
 C
C
 )= A−1δA (1 − A−1δA )≤ A−1 δA
)= A−1δA (1 − A−1δA )≤ A−1 δA 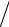 (1 − A−1 δA ).
(1 − A−1 δA ).
Использование полученных оценок позволяет получить выражение

 δx
δx
 ≤
≤ 
 A−1
A−1 
 (
(
 δf
δf 
 +
+ 
 δA
δA


 x
x
 )
)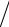 (1 −
(1 − 
 A−1
A−1 


 δA
δA
 ).
).
Учитывая, что

 δf
δf 
 =
= 
 δf
δf 
 (
(
 Ax
Ax

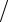

 f
f 
 )≤
)≤ 
 δf
δf 


 A
A


 x
x

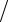

 f
f 
 ,
,
оценка принимает вид

 δx
δx
 ≤
≤ 
 A−1
A−1 
 (
(
 δf
δf 


 A
A


 x
x

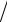

 f
f 
 +
+ 
 δA
δA


 x
x
 )
)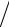 (1 −
(1 − 
 A−1
A−1 


 δA
δA
 )= =
)= = 
 A−1
A−1 


 A
A
 (
(
 δf
δf 

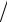

 f
f 
 +
+ 
 δA
δA

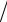

 A
A
 )
)
 x
x

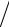 (1 −
(1 − 
 A−1
A−1 


 A
A


 δA
δA

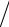

 A
A
 ).
).
Поскольку M A = 
 A−1
A−1 


 A
A
 , получается доказываемое утверждение теоремы:
, получается доказываемое утверждение теоремы:

 δx
δx

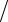

 x
x
 ≤ M A (
≤ M A (
 δA
δA

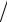

 A
A
 +
+ 
 δf
δf 

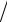

 f
f 
 )
)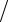 (1 − M A
(1 − M A 
 δA
δA

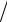

 A
A
 ).
).
2.2. Полиномы Чебышёва1
Вводится, согласно [8], норма
f = max f (x) ,
x [a,b]
называемая чебышёвской. Рассматривается следующая задача: среди всех полиномов степени n со старшим коэффициентом, равным 1, найти такой много-
член T (x) , для которого величина |
|
|
|
T |
|
|
|
= max |
|
T (x) |
|
минимальна. Такой много- |
|
|
|
|
|
|
|||||||
n |
|
|
|
n |
|
|
|
x [−1,1] |
|
n |
|
|
|
|
|
|
|
|
|
||||||
член носит название полинома Чебышёва. |
|
|
||||||||||
Для решения поставленной задачи строится функция |
||||||||||||
Pn (x) = cos(narccos(x)). |
(2.5) |
|||||||||||
Выполняя тригонометрические преобразования
Pn+1 (x) = cos((n +1)arccos(x))= cos(narccos(x)+ arccos(x))=
=cos(narccos(x))cos(arccos(x))− sin(narccos(x))sin(arccos(x)) =
1Чебышёв Пафнутий Львович [4.5.1821 – 26.11.1894]. В 1841 году закончил Московский университет и там же в 1846 году защитил магистерскую диссертацию. В 1847 году подготовил и защитил диссертацию на право чтения лекций и был утвержден в звании доцента Петербургского университета. В1849 году защитил докторскую диссертацию; в 1850 году стал профессором Петербургскогоуниверситета. С1856 годаявлялсяакадемикомПетербургскойакадемиинаук.
27
= xPn (x) − sin(narccos(x))sin(arccos(x)),
Pn−1 (x) = cos((n −1)arccos(x)) = cos(narccos(x) − arccos(x))=
=cos(narccos(x))cos(arccos(x))+ sin(narccos(x))sin(arccos(x))=
=xPn (x) + sin(narccos(x))sin(arccos(x))
искладывая почленно два последних равенства
Pn+1 + Pn−1 = 2xPn , |
Pn+1 = 2xPn − Pn−1 , |
Pn+1 . В соот- |
|
получают рекуррентное соотношение для построения функции |
|||
ветствии с формулой (2.5) |
P0 (x) = cos(0 arccos(x))=1, |
|
|
|
|
||
|
P1 (x) = cos(1 arccos(x))= x . |
|
|
И далее, в соответствии с полученной зависимостью, |
|
||
P |
(x)= 2xP (x) |
− P (x)= 2x2 −1, |
|
2 |
1 |
0 |
|
P (x) = 2xP (x)− P (x)= 4x3 − 3x , |
|
||
3 |
2 |
1 |
|
P (x)= 2xP (x)− P (x) =8x4 −8x2 +1 |
|
||
4 |
3 |
2 |
|
P5 (x)= 2xP4 (x) − P3 (x)=16x5 − 20x3 + 3x, … |
|
||
Можно заметить, что в общем случае коэффициент при старшей степени |
|||
определяется следующим образом: |
|
|
|
Pn (x) = 2xPn−1 (x)− Pn−2 (x) = 2n−1 xn +… |
(2.6) |
||
Искомая функция Tn (x) определяется в виде |
|
||
T (x) = 21−n P (x) = 21−n cos(narccos(x)). |
(2.7) |
||
n |
n |
|
|
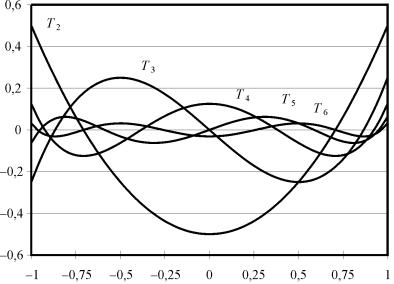
Очевидно, что Tn (x) является полиномом степени n со старшим коэффициентом, равным 1. На рис. 2.1 показаны некоторые из полиномов Tn (x) построенной системы.
Рис. 2.1. Полиномы Tn (x) при n = 2, 3, 4, 5, 6
28

Корни полинома (табл. 2.1) определяются из уравнения cos(narccos(x))= 0 .
Поскольку Tn (x) – полином степени n, он имеет не более n корней, причем
все они различны и лежат на отрезке [–1, 1]:
xk = cos((2k −1)π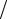 2n), k =1,n .
2n), k =1,n .
Вполне очевидно (см. рис. 2.1), что полиномы Tn (x) принимают экстремальные значения в тех точках, где функция cos принимает значения +1 или –1:
cos(narccos(x))= ±1, narccos(xp )= pπ,
xp = cos(pπ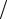 n), p = 0,n .
n), p = 0,n .
Таблица 2.1
Корни полинома Tn (x) для n = 1, 2, 3, 4, 5, 6, 7
n = 1 |
n = 2 |
n = 3 |
n = 4 |
n = 5 |
n = 6 |
n = 7 |
||
|
|
|
|
|
|
|
|
|
0,0 |
0,707107 |
0,866025 |
0,923879 |
0,951057 |
0,965926 |
0,974928 |
||
|
|
|
|
|
|
|
|
|
– |
– 0,707107 |
0,0 |
0,382683 |
0,587785 |
0,707107 |
0,781831 |
||
|
|
|
|
|
|
|
|
|
– |
– |
– 0,866025 |
– 0,382683 |
0,0 |
0,258819 |
0,433884 |
||
|
|
|
|
|
|
|
|
|
– |
– |
– |
– 0,923879 |
– 0,587785 |
– 0,258819 |
0,0 |
||
|
|
|
|
|
|
|
|
|
– |
– |
– |
– |
– 0,951057 |
– 0,707107 |
– 0,433884 |
||
|
|
|
|
|
|
|
|
|
– |
– |
– |
– |
– |
– 0,965926 |
– 0,781831 |
||
|
|
|
|
|
|
|
|
|
– |
– |
– |
– |
– |
– |
– 0,974928 |
||
|
|
|
|
|
|
|
|
|
В этих точках каждый из полиномов Tn (x) принимает чередующиеся по |
||||||||
знаку значения Tn (xp ) = (−1)р 21−n , p = |
|
; |
при этом чебышёвская норма равна |
|||||
0,n |
||||||||

 Tn
Tn 
 = 21−n .
= 21−n .
Лемма 2.2. Пусть система точек −1 ≤ x0 < x1 <…< xn−1 < xn ≤ 1 такова, что
Qn (xp ) = 
 Qn
Qn 
 , p = 0,n , причем в этих точках функция Qn (xp ) имеет чередую-
, p = 0,n , причем в этих точках функция Qn (xp ) имеет чередую-
щиеся знаки. Тогда среди всех полиномов степени n со старшим коэффициентом, равным 1, многочлен Qn (x) наименее уклоняется от 0.
29
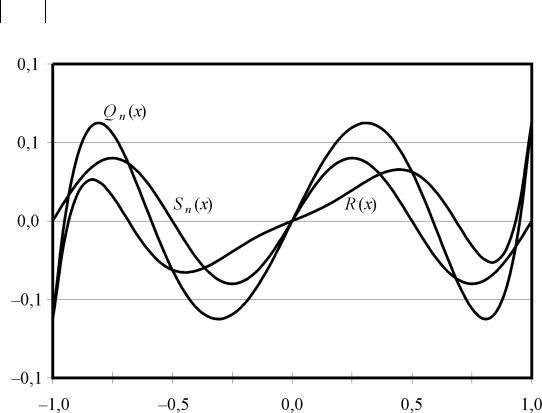
Доказательство. Предполагается, что существует полином Sn (x) степени n со старшим коэффициентом, равным 1 (рис. 2.2), причем 
 Sn
Sn 
 <
< 
 Qn
Qn 
 , то есть Sn (x) <
, то есть Sn (x) < 
 Qn
Qn 
 x [−1,1]. Вводится функция R(x) = Qn (x) − Sn (x) , отличная от нуля и являющаяся полиномом степени n – 1.
x [−1,1]. Вводится функция R(x) = Qn (x) − Sn (x) , отличная от нуля и являющаяся полиномом степени n – 1.
Рис. 2.2. Полиномы Qn(x), Sn(x) и R(x) = Qn (x) −Sn (x)
В точках экстремумов xp |
функция Qn(x) принимает значения |
|||||||||||||||||||
Q (x |
|
) = (−1)p |
|
Q |
|
, |
|
p = |
|
. |
|
|
||||||||
p |
|
|
0,n |
|||||||||||||||||
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда в тех же точках R(x |
|
) = (−1)p |
|
Q |
|
− S |
|
(x |
|
), p = |
|
, и в силу пред- |
||||||||
p |
|
|
n |
p |
0,n |
|||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||
положения функция R(x) на отрезке [–1, 1] меняет знак n раз, а значит, имеет n корней, чего не может быть, поскольку R(x) является полиномом степени n – 1.
Таким образом, утверждение леммы 2.2 доказано.
Поскольку построенный ранее полином Чебышёва Tn (x) удовлетворяет всем требованиям леммы, именно он является наименее уклоняющимся от нуля на отрезке [–1, 1].
В случае необходимости отыскания полинома со старшим коэффициентом, равным 1, наименее уклоняющегося от нуля на произвольном отрезке [a, b], следует перейти к новой переменной
t = 2x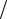 (b − a)− (b + a)
(b − a)− (b + a)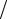 (b − a), a ≤ x ≤ b ,
(b − a), a ≤ x ≤ b ,
30
