ϕ = c0′ϕ0 + c1′ϕ1 +…+ cm′ ϕm = 0 , и из условия линейной независимости системы
функций ϕk H , k = 0,m , вытекает: c0′ = 0, c1′ = 0,…, c′m = 0 . Но это означает, что (Ac,c)> 0 c ≠ 0, то есть матрица А является положительно определенной.
Теорема 4.4. Если А – симметричная положительно определенная матрица, fˆ – заданный вектор, то функционал (4.29) имеет единственную точку ми-
нимума c~ тогда и только тогда, когда вектор c~ удовлетворяет системе линейных алгебраических уравнений
Доказательство. В силу положительной определенности матрица А имеет определитель, отличный от нуля, то есть система уравнений (4.30) разрешима и имеет единственное решение.
Достаточность теоремы. Пусть вектор c~ является решением системы уравнений (4.30). Для произвольного вектора v, согласно определению (4.29), имеет место следующее выражение:
F (c + v) = (A(c + ν),c + v) − 2( fˆ,c + v)=
= (Ac , c )+ (Ac , v)+ (Av, c )+ (Av, v)− 2 |
( fˆ,c)− 2 |
( fˆ,v). |
~ ~ |
~ |
~ |
|
|
С учетом симметрии A и вида функционала (4.29) можно записать |
F(c + v) = (Ac , c )+ 2(Ac ,v)+ (Av,v)−2 |
( fˆ,c)− 2 |
( fˆ,v) = |
~ |
~ ~ |
~ |
|
|
= ( Ac,c) + 2 ( Ac,v) −( fˆ,v) + ( Av,v) − 2( fˆ,c) =
( Av,v) + 2(Ac − fˆ,v)+ ( Ac,c) − 2( fˆ,c) = ( Av,v) + 2(Ac − fˆ,v)+ F (c).
Если принять во внимание выражение (4.30), то окончательно получается
F(c + v) = (Av,v)+ F(c ). |
|
~ |
|
~ |
|
|
Положительная определенность матрицы А позволяет привести последнее |
~ |
~ |
v R |
n+1 |
, но это и означает мини- |
выражение к неравенству F(c + v) > F(c ) |
|
мальность функционала (4.29) в точке c . |
|
|
|
Необходимость. Пусть вектор c |
~ |
|
|
|
доставляет минимум функционалу (4.29). |
~ |
|
|
|
|
Если в представленном выше равенстве
F(c + v)= (Av, v)+2(Ac − fˆ,v)+ F (c) |
~ |
|
положить v = λu, u Rm+1 |
– произвольный вектор, λ – скаляр, то |
F(c + λu) = λ (Au, u) + 2λ(Ac − fˆ,u)+ F (c). |
~ |
2 |
Полученное выражение можно рассматривать как скалярную функцию g(λ)= λ2 (Au, u)+ 2λ(Ac − fˆ,u)+ F (c)
аргумента λ. В силу принятого допущения о минимальности функционала
(4.29) имеет место неравенство |
~ |
~ |
F(c |
+ λu) > F(c ), то есть g(λ)> g(0) λ. |
Это, в свою очередь, означает, что λ = 0 доставляет минимум функ- |
ции g(λ), откуда следует |
dg |
(λ) dλ |
|
λ=0 = 0, |
|
|
gλ′ (0) = 2λ( Au,u) + 2 |
(Ac − fˆ,u) |
= 2(Ac − fˆ,u)= 0. |
|
|
|
|
|
|
λ=0 |
Из справедливости последнего равенства u Rm+1 следует:
Ac − fˆ = 0,
что и требовалось доказать.
В компонентной записи система линейных алгебраических уравнений выглядит следующим образом:
|
m |
~ |
|
|
|
|
|
= (f , ϕj )H , j = 0,m . |
(4.31) |
|
∑ck (ϕk , ϕj )H |
|
k=0 |
|
|
|
|
|
Алгоритм определения элемента наилучшего приближения: а) вычисляются коэффициенты матрицы:
akj = (ϕk ,ϕj )H = ∫b ϕk (x)ϕj (x)dx, k, j = 0,m ;
a
б) подсчитываются значения правых частей:
f j = (f , ϕj )H = ∫b |
f (x)ϕj (x)dx, j = |
|
; |
0,m |
a |
|
|
|
в) решается система линейных алгебраических уравнений (4.31);
m
~ ∑~
г) строится обобщенный полином ϕ = ck ϕk.
k=0
Вслучае ортонормированности системы ϕk , k = 0,m , построение прибли-
~ |
|
|
|
|
|
|
поскольку в этом случае akj = (ϕk ,ϕj )H |
= δkj , и компо- |
жения ϕ упрощается, |
~ |
определяются формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ненты вектора ck |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 0,m . |
|
|
|
|
|
ck = ( f ,ϕk )H = ∫ f (x)ϕk (x)dx, |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Погрешность приближения оценивается выражением |
|
|
|
~ |
|
|
|
2 |
~ |
~ |
|
|
|
|
|
|
|
2 |
~ |
|
|
|
|
|
~ |
|
|
|
2 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f − ϕ |
|
|
|
H |
= ( f − ϕ, f |
− ϕ)H = |
|
|
|
f |
|
|
|
H − 2( f , ϕ)H |
+ |
|
|
|
ϕ |
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|

= |
|
|
f |
|
|
|
2 |
m ~ |
|
m ~ ~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
− 2∑ck ( f , ϕk )H + |
∑ck cj (ϕk ,ϕj )H = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =0 |
|
k, j =0 |
|
|
|
|
|
|
|
|
|
= |
|
f |
|
|
|
|
2 |
m ~2 |
m ~ ~ |
|
|
|
|
2 |
m ~2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
−2∑ck |
+ ∑ck cj δkj = |
f |
|
|
H |
−∑ck . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=0 |
k, j=0 |
|
|
|
|
|
k=0 |
|
|
|
|
|
~ |
|
m |
~ |
|
|
|
|
|
|
|
1 |
, где |
~ |
|
|
– |
|
|
|
|
|
|
|
|
|
|
Разложение ϕ = |
∑ck ϕk называется полиномом Фурье |
ck , k = 0,m |
k=0
коэффициенты Фурье.
Пример 4.3. Для функции f (x) = x на отрезке [–1, 1] построить наилучшее приближение в гильбертовом пространстве с использованием полинома P4.
Cистема линейно-независимых функций – полиномы ϕk (x)= xk , k = 0,4 .
В соответствии с приведенными соотношениями вычисляются коэффициенты akj и fj системы линейных алгебраических уравнений:
|
|
1 |
|
xk+ j+1 |
|
|
1 |
|
|
|
1 |
|
|
[1 − (−1)k+ j+1 ], |
|
|
|
|
|
|
|
|
|
|
|
akj = (ϕk ,ϕj )H = ∫ xk x j dx = |
|
|
|
|
|
= |
|
|
|
|
|
|
k + j +1 |
|
|
|
k |
+ j +1 |
|
|
|
|
|
|
−1 |
|
|
−1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
[1+(−1)j+2 |
]. |
|
0 |
1 |
|
|
|
x j+2 |
|
|
x j+2 |
|
|
|
|
|
|
|
|
|
|
|
f j = (f ,ϕj )H = ∫ |
|
x |
|
x jdx = −∫x j+1dx +∫x j+1dx = − |
|
|
+ |
|
|
= |
1 |
|
|
|
|
|
|
|
|
|
j +2 |
j +2 |
|
|
|
|
j +2 |
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
−1 |
0 |
|
|
|
|
|
|
−1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Числовые значения коэффициентов приведены в табл. 4.3.
Таблица 4.3 Коэффициенты матрицы akj и правая часть fj системы линейных алгебраических
уравнений Ac = fˆ при построении наилучшего приближения
|
j = 0 |
1 |
2 |
3 |
4 |
fi |
|
|
|
|
|
|
|
k = 0 |
2,0 |
0,0 |
0,666667 |
0,0 |
0,4 |
1,0 |
1 |
0,0 |
0,666667 |
0,0 |
0,4 |
0,0 |
0,0 |
2 |
0,666667 |
0,0 |
0,4 |
0,0 |
0,285714 |
0,5 |
3 |
0,0 |
0,4 |
0,0 |
0,285714 |
0,0 |
0,0 |
4 |
0,4 |
0,0 |
0,285714 |
0,0 |
0,222222 |
0,333333 |
|
|
|
|
|
|
|
Решение системы уравнений (4.30) методом Гаусса позволило построить полином P4, аппроксимирующий на отрезке [–1, 1] функцию f (x) = x :
1 Фурье Жан Батист Жозеф [21.3.1768 – 16.5.1830] – французский математик. Окончил военную школу в Осере, там же работал преподавателем. В 1796–1798 годах преподавал в Политехнической школе в Париже. В 1798 году принимал участие в Египетской экспедиции Наполеона Бонапарта. В 1802–1815 годах был префектом департамента Изер. С 1817 года избран членом Парижской академии наук. В 1829 году стал иностранным почетным членом Петербургской академии наук.
P4 (x) = 0,1172 +1,6406x2 −0,8203x4 .
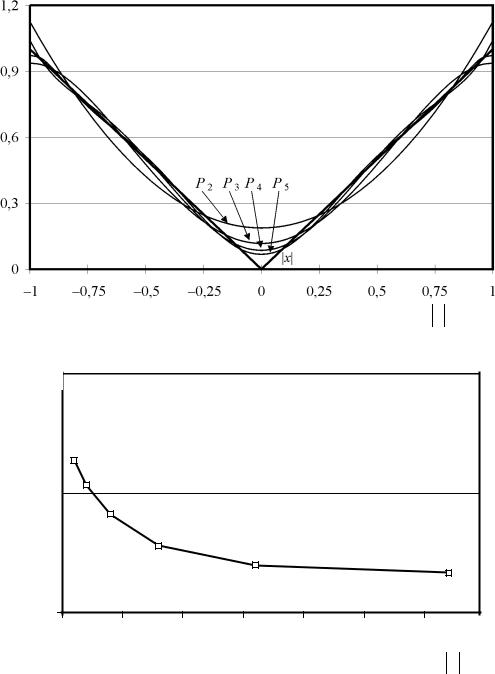
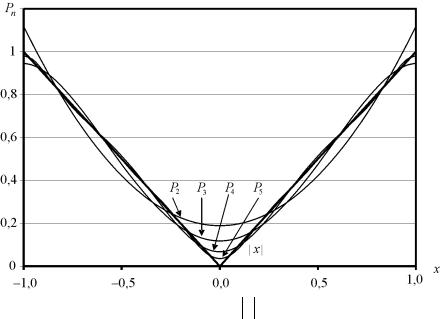
Аналогичным образом строятся полиномы P2(x), P3(x), P5(x) и другие. Вид этих функций приведен на рис. 4.6. На рис. 4.7 показана зависимость погреш-
ности |
|
|
|
f − Pm |
|
|
|
= max |
|
f (x)− Pm (x) |
|
аппроксимации функции f (x) = |
|
x |
|
от степе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [−1,1] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ни m полиномов Pm(x).
Рис. 4.6. Наилучшие приближения функции f (x) = x |
|
на отрезке [–1, 1] полиномами P2(x), P3(x), P4(x) и P5(x) |
|
|| f –P1m || |
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
0,01 |
|
|
|
|
|
|
m |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
Рис. 4.7. Погрешность аппроксимации функции |
f (x) = x |
|
на отрезке [–1, 1] полиномами Pm(x) наилучшего приближения |
4.4. Метод наименьших квадратов

В практических исследованиях часто возникает ситуация, когда необходимо аппроксимировать табличные значения f (xi )= fi , i = 0,n с помощью приближения ϕ(x), содержащего определяемые коэффициенты ck , k = 0,m
в количестве меньшем, чем число узловых точек: m < n. По этой причине, в отличие от рассмотренных ранее способов аппроксимации функции полиномами Ньютона, Лагранжа, Эрмита, сплайнами, не используется условие равенства значений функции f(x) и ее приближения ϕ(x) в узлах разностной сетки. В методе наименьших квадратов близость аппроксимирующего многочлена заданной функции оценивается с помощью какой-либо нормы, то есть в среднем для всего отрезка, на котором строится аппроксимация.
Пусть известен набор значений |
f (xi )= fi , i = |
|
|
|
функции для некоторых |
0,n |
значений ее аргумента. В линейном пространстве Rn+1 |
скалярное произведение |
и норма определяются выражениями |
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
(u,v) = ∑uivi , |
|
|
|
u |
|
|
|
= |
(u,u) = ∑uiui , |
u,v Rn+1 . |
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
i=0 |
|
Отыскиваемое приближение ϕ(x; c0 , c1,…, cm ) зависит от известного числа |
m +1 параметров c0 , c1,…, cm . Степень отклонения функции f(x) от ее приближения ϕ(x) определяется соотношением
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f − ϕ |
|
|
|
2 = |
|
|
|
f |
|
|
|
2 − 2( f , ϕ)+ |
|
|
|
ϕ |
|
|
|
2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
(4.32) |
= ∑ fi2 − 2∑ fiϕ(xi ; c0 , c1 ,…, cm )+ ∑ϕ2 |
(xi ; c0 , c1,…, cm ). |
i=0 |
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=0 |
|
|
|
|
|
Для определения наименьшего отклонения используются необходимые условия минимума функции нескольких переменных:
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
n |
|
|
|
|
|
|
f |
− ϕ |
|
|
|
|
|
|
|
|
|
= −2∑ fi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂c0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
i=0 |
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
f |
− ϕ |
|
|
|
|
|
|
|
|
= −2∑ fi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂c1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
f − ϕ |
|
|
|
2 |
= −2∑ fi |
|
|
|
|
|
∂c |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=0 |
∂ϕ(xi ;c0 ,c1,…,cm ) + 2 |
n |
|
ϕ(x |
;c |
,c |
,…,c |
m |
|
)∂ϕ(xi ;c0 ,c1,…,cm ) |
|
= 0, |
∂c0 |
∑ |
|
i |
|
0 |
|
1 |
|
|
|
|
∂c0 |
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ϕ(xi ;c0 ,c1,…,cm ) + 2 |
n |
ϕ(x |
;c |
,c ,…,c |
m |
)∂ϕ(xi ;c0 ,c1,…,cm ) |
= 0, |
∑ |
|
|
i |
|
0 |
|
1 |
|
|
|
∂c1 |
|
|
∂c1 |
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ϕ(xi ;c0 ,c1,…,cm ) + 2 n |
|
|
ϕ(x |
|
;c |
|
,c |
|
,…,c |
m |
)∂ϕ(xi ;c0 ,c1,…,cm ) |
= 0. |
∂cm |
∑ |
i |
0 |
1 |
|
|
|
∂cm |
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Иными словами, речь идет о решении системы алгебраических уравнений, нелинейных в общем случае:
∑( fi − ϕ(xi ;c0 ,c1,…,cm ))∂ϕ(xi ;c0 ,c1,…,cm ) = 0, |
n |
|
|
|
|
i=0 |
∂c0 |
,…,cm ) |
|
n |
∂ϕ(xi ;c0 ,c1 |
= 0, |
∑( fi − ϕ(xi ;c0 ,c1,…,cm )) |
∂c1 |
|
i=0 |
|
|
|
|
|
|
|
n |
∂ϕ(xi ;c0 ,c1 |
,…,cm ) |
|
∑( fi − ϕ(xi ;c0 ,c1,…,cm )) |
∂c |
m |
|
= 0. |
i=0 |
|
|
|
В частном случае, когда приближение ϕ(x) представимо в виде
m
ϕ(x;c0 ,c1,…,cm )= ∑ck ϕk (x),
k =0
оценка (4.32) отклонения функции от ее приближения записывается в форме
|
f − ϕ |
|
2 |
|
|
|
n |
|
|
|
n |
m |
|
n |
m |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∑ fi2 − 2∑ fi ∑ck ϕk (xi )+ ∑ ∑ck ϕk (xi )∑c j ϕj (xi ) . |
|
|
|
|
|
|
|
|
i=0 |
|
|
|
i=0 k=0 |
|
i=0 |
k=0 |
j=0 |
|
Условие минимальности отклонения приближения от функции записыва- |
ется аналогично представленному выше: |
|
|
|
|
|
|
∂ |
|
|
|
|
|
2 |
n |
|
n |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f − ϕ |
|
|
|
= −2∑ fiϕ0 |
(xi )+ 2∑ ϕ0 (xi )∑ck ϕk (xi ) |
= 0, |
|
∂c0 |
|
|
|
|
|
|
|
|
|
|
|
i=0 |
|
i=0 |
|
k=0 |
|
|
|
|
∂ |
|
|
|
|
|
2 |
n |
|
n |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f − ϕ |
|
|
|
= −2∑ fiϕ1 (xi ) + 2∑ |
ϕ1 (xi )∑ck ϕk (xi ) = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
∂c1 |
|
|
|
|
|
|
i=0 |
|
i=0 |
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
n |
|
n |
|
m |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂cl |
|
|
f − ϕ |
|
|
|
= −2∑ fiϕm (xi )+ 2∑ ϕm (xi )∑ck ϕk (xi ) |
= 0. |
|
|
|
|
|
|
|
|
i=0 |
|
i=0 |
k=0 |
|
|
В итоге получена система линейных алгебраических уравнений относи-
тельно коэффициентов разложения |
ck , |
k = |
|
: |
|
|
|
0,m |
|
|
|
|
n |
n |
|
|
|
|
|
|
n |
n |
|
(xi ), |
c0 ∑ϕ0 |
(xi )ϕ0 (xi )+ c1 ∑ϕ1 (xi )ϕ0 (xi ) |
+…+ cm ∑ϕm (xi )ϕ0 (xi )= ∑ fiϕ0 |
|
i=0 |
i=0 |
|
|
|
|
|
|
i=0 |
i=0 |
|
|
|
n |
n |
|
|
|
|
|
|
n |
n |
(xi ), |
c0 |
∑ϕ0 |
(xi )ϕ1 (xi )+ c1 ∑ϕ1 (xi )ϕ1 (xi )+…+ cm ∑ϕm (xi )ϕ1 (xi ) |
= ∑ fiϕ1 |
|
i=0 |
i=0 |
|
|
|
|
|
|
i=0 |
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
n |
n |
|
|
c0 |
∑ϕ0 |
(xi )ϕm (xi )+ c1 ∑ϕ1 (xi )ϕm |
(xi )+…+ cm ∑ϕm (xi )ϕm (xi )= ∑ fiϕm (xi ). |
|
i=0 |
i=0 |
|
|
|
|
|
|
i=0 |
i=0 |
|
|
Пример приближения функции |
|
x |
|
|
полиномами на отрезке [–1, 1] с исполь- |
|
|
зованием метода наименьших квадратов приведен на рис. 4.8. |
|
|
|
Рис. 4.8. Приближение функции x полиномами P2(x), P3(x), P4(x) и P5(x) методом наименьших квадратов
Рассмотренные в настоящей главе вопросы не исчерпывают всего многообразия известных способов аппроксимации функций. Способы приближения функций, применяемые при построении решений дифференциальных уравнений в частных производных методом Галеркина, рассматриваются в 13-й главе, посвященной аппроксимации кусочно-гладкими функциями.
Контрольные вопросы и задания
4.1.Сформулируйте задачу аппроксимации. Каковы условия разрешимости этой задачи?
4.2.Укажите требования к аппроксимирующим функциям. В каком случае интерполяция называется линейной?
4.3.Что представляют собой разделенные разности? Поясните их геометрический смысл.
4.4.Укажите порядок построения интерполяционного полинома Ньютона.
4.5.Укажите порядок построения интерполяционного полинома Лагранжа.
4.6.Покажите, что полиномы Ньютона и Лагранжа, построенные на одном множестве табличных значений функции, тождественны.
4.7.Укажите условия сходимости процесса интерполяции полиномами. Приведите примеры.
4.8.Обоснуйте преимущества метода интерполяции для решения нелинейного уравнения.
117
4.9.Опишите способ решения нелинейного уравнения с помощью обратной интерполяции.
4.10.Укажите порядок построения интерполяционного многочлена Эрмита.
4.11.Опишите идею сплайн-аппроксимации функции и порядок построения кубического сплайна.
4.12.Что понимается под сходимостью процесса интерполяции кубическими сплайнами? Сформулируйте и докажите лемму об оценке сходимости по «сеточной» норме.
4.13.Сформулируйте и докажите теорему о сходимости процесса интерполяции функции кубическими сплайнами.
4.14.Опишите порядок построения наилучшего приближения функции
сиспользованием теории гильбертовых пространств.
4.15.В чем заключается метод наименьших квадратов для аппроксимации функции, заданной таблично?

5. АЛГЕБРАИЧЕСКАЯ ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ
Рассматривается квадратная матрица А размером m × m. Если существуют
такие векторы X Rm , X ≠ 0 , что |
|
AX = λX , |
(5.1) |
то скаляр λ называется собственным значением, а X – собственным вектором
матрицы A, соответствующим собственному значению λ. В иной записи
AX − λX = (A − λE)X = 0, X ≠ 0. |
|
|
|
(5.2) |
Система линейных однородных алгебраических уравнений (5.2) имеет не- |
тривиальное решение в случае |
|
|
|
|
|
|
|
|
|
a11 − λ |
|
a12 |
a1m |
|
|
|
a |
|
a |
|
− λ |
a |
|
|
|
|
|
|
|
|
= 0 . |
det(A − λE)= det |
|
21 |
|
22 |
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
am1 |
|
am2 |
|
|
|
|
|
|
amm − λ |
|
Характеристический многочлен |
det(A − λE) является полиномом степе- |
ни m относительно переменной λ. Это, в свою очередь, означает, что существует m корней характеристического многочлена и, следовательно, имеется m соб-
ственных значений |
λi |
и m соответствующих им |
собственных векторов |
X (i), i = |
|
, для матрицы A. |
|
|
|
|
|
1,m |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
. |
|
Пример 5.1. Задана матрица A = |
|
|
|
|
|
|
|
|
5 |
4 |
|
|
|
|
|
|
|
|
|
|
|
Определить собственные значения и векторы этой матрицы. |
Характеристический многочлен |
|
|
|
|
|
|
1 − λ |
2 |
|
|
|
|
|
|
|
|
|
|
− λ)(4 − λ)−10 = λ2 |
− 5λ − 6 |
|
|
det |
5 |
|
= (1 |
|
|
|
4 − λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
позволяет определить собственные значения
λ1 = (5 +  49) 2 = 6, λ2 = (5 −
49) 2 = 6, λ2 = (5 −  49)
49)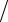 2 = −1.
2 = −1.
Система уравнений для определения первого собственного вектора, соответствующего λ1 = 6 :
−5X1(1) + 2X2(1) = 0,
5X1(1) − 2X2(1) = 0,
где X1(1), X 2(1) – компоненты собственного вектора X (1) . Последняя система со-
держит линейно зависимые уравнения (как это и следовало ожидать для системы линейных алгебраических уравнений с определителем, равным нулю). Из любого уравнения этой системы можно найти X1(1) = 2X 2(1)  5. Для однозначности определения собственных векторов принимается условие нормирования,
5. Для однозначности определения собственных векторов принимается условие нормирования, 
 X (i)
X (i) 
 =1, i =1,m , то есть
=1, i =1,m , то есть

 X (1)
X (1) 
 =
=  [X1(1) ]2 + [X 2(1) ]2 =
[X1(1) ]2 + [X 2(1) ]2 =  4[X 2(1) ]2
4[X 2(1) ]2  25 + [X 2(1) ]2 = X 2(1)
25 + [X 2(1) ]2 = X 2(1)  29 5 =1,
29 5 =1,
|
1 |
2 |
0,371391 |
X (1) = |
|
|
|
29 |
|
= |
. |
|
5 |
0,928477 |
|
|
|
|
|
Система уравнений для определения второго собственного вектора, соответствующего λ2 = −1:
|
|
|
|
|
|
2X (2) |
+ 2X (2) = 0, |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
5X (2) |
+ 5X (2) = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
Отсюда следует связь между компонентами второго собственного вектора: |
X1(2) = −X 2(2) . Из условия нормирования вектора получается: |
|
X (2) |
|
|
|
= [X1(2) ]2 + [X 2(2) ]2 = [X 2(2) ]2 + [X 2(2) ]2 = X 2(2) 2 =1, |
|
|
|
|
|
|
|
|
|
|
2 |
−1 |
|
− 0,707107 |
|
|
|
|
|
X (2) = |
|
|
|
|
|
|
|
|
|
|
2 |
|
= |
. |
|
|
|
|
|
|
1 |
|
|
0,707107 |
|
|
|
|
|
|
|
|
|
|
|
|
5.1. Устойчивость собственных значений и векторов
Наряду с матрицей A рассматривается матрица AT . Собственные числа обеих матриц одинаковы. Собственные векторы матриц обозначаются,
соответственно, X (i) и Y ( j ),
AX (i) = λi X (i ), AT Y ( j ) = λ jY ( j ).
Разность скалярных произведений (AT Y ( j ), X (i ) ) и (Y ( j ), AX (i) ),
(Y ( j ), AX (i ) )− (AT Y ( j ), X (i) )= (Y ( j ),λi X (i) )− (λ jY ( j ), X (i ) )= (λi − λ j )(Y ( j ), X (i) ),
с учетом равенства
(Y ( j ), AX (i) )= (AT Y ( j ), X (i ) ) |
(5.3) |
приводит к выражению
(λi − λ j )(Y ( j ), X (i) )= 0,


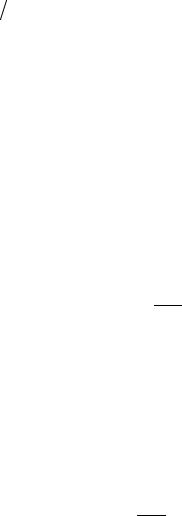





 49
49 49
49 2
2  5. Для однозначности определения собственных векторов принимается условие нормирования,
5. Для однозначности определения собственных векторов принимается условие нормирования,