Пример 5.6. Определить наибольшее и наименьшее собственные значения
Рассматривается итерационный процесс Z (s+1) = AZ (s) . Для заданной матрицы формируется система уравнений
Z (s+1) |
= Z (s) + 2Z (s) , |
|
1 |
1 |
2 |
|
|
= 5Z (s) + 4Z (s) . |
Z (s+1) |
|
2 |
1 |
2 |
1
В качестве первого приближения выбирается вектор Z (0) = . Результаты
1
расчетов сведены в табл. 5.3.
|
|
|
|
|
|
|
|
|
Таблица 5.3 |
Вычисление наибольшего собственного значения матрицы А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
Z1(s) |
Z2(s) |
|
Z (s ) |
|
|
|
|
|
|
λ(s) |
|
|
|
|
|
|
|
итерации |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1,0 |
1,0 |
1,414214 |
|
|
– |
|
|
|
|
|
1 |
3,0 |
9,0 |
9,486833 |
6,708204 |
|
|
|
|
|
2 |
21,0 |
51,0 |
55,15433 |
5,813777 |
|
|
|
|
|
3 |
123,0 |
309,0 |
332,5808 |
6,030004 |
|
|
|
|
|
4 |
741,0 |
1851,0 |
1993,811 |
5,994967 |
|
|
|
|
|
5 |
4443,0 |
11109,0 |
11964,54 |
6,000838 |
|
|
|
|
|
6 |
26661,0 |
66651,0 |
71785,55 |
5,99986 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После нормирования получается вектор
|
|
|
|
|
|
|
(6) |
0,371398 |
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
= |
. |
|
|
|
|
|
|
|
|
0,928474 |
|
|
|
|
|
|
|
|
|
|
|
Для нахождения наименьшего собственного значения используется матри- |
|
|
−1 |
= |
1 |
− 4 |
2 |
|
|
|
ца |
A |
|
|
|
. |
|
|
|
|
6 |
|
|
|
|
|
|
|
5 |
− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно выражению (5.11) строится итерационная процедура

Z (s+1) |
= (− 4Z (s) + 2Z (s) ) 6, |
|
1 |
1 |
2 |
|
|
|
= (5Z (s) |
− Z (s) ) |
6. |
Z (s+1) |
|
2 |
1 |
2 |
|
1
В качестве первого приближения выбирается вектор Z (0) = . Результаты
1
расчетов сведены в табл. 5.4.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.4 |
Вычисление наибольшего собственного значения матрицы А–1 |
Номер ите- |
|
Z1(s) |
|
|
Z2(s) |
|
|
|
Z (s ) |
|
|
|
|
|
|
|
μ(s ) |
|
|
|
|
|
|
|
|
|
рации |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1,0 |
|
|
|
1,0 |
|
|
1,414214 |
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
–0,333333 |
|
|
0,666667 |
|
|
0,745356 |
|
0,527046 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0,444444 |
|
|
–0,388889 |
|
|
0,590564 |
|
0,792324 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
–0,425926 |
|
|
0,435185 |
|
|
0,608933 |
|
1,031104 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
0,429012 |
|
|
–0,427469 |
|
|
0,605625 |
|
0,994568 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
–0,428498 |
|
|
0,428755 |
|
|
0,606171 |
|
1,000899 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
0,428584 |
|
|
–0,428541 |
|
|
0,606079 |
|
0,999851 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
–0,428569 |
|
|
0,428577 |
|
|
0,606094 |
|
1,000025 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
0,428572 |
|
|
–0,428571 |
|
|
0,606091 |
|
1,000021 |
|
|
|
|
|
|
|
|
|
|
|
9 |
|
–0,428571 |
|
|
0,428572 |
|
|
0,606092 |
|
1,000001 |
|
|
|
|
|
Собственный вектор матрицы A–1после нормирования имеет вид |
|
|
|
|
|
|
− 0,707107 |
|
|
|
|
|
|
|
|
|
Z |
(9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
0,707107 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А равен |
Модуль |
наименьшего собственного |
значения матрицы |
|
|
μ(s) −1 = 0,999999. Точные значения наибольшего и наименьшего собственных
значений, компонент собственных векторов определены в примере 5.1.
Контрольные вопросы и задания
5.1. Сформулируйте алгебраическую проблему собственных значений. Укажите различие между полной и частичной проблемами.
5.2.Что понимается под устойчивостью собственных значений и собственных векторов?
5.3.Поясните, что называется коэффициентом перекоса, и укажите его геометрический смысл.
5.4.Опишите и обоснуйте метод интерполяции для определения собственных значений матрицы.
5.5.Обоснуйте алгоритм приближенного определения собственных векторов матрицы.
5.6.Опишите процедуру метода линеаризации для поиска собственных значений и векторов.
5.7.Можно ли при использовании степенного метода определить знак максимального собственного значения?
5.8 Поясните идею определения минимального собственного значения с помощью «обратных итераций».
6.ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
6.1.Разностная аппроксимация
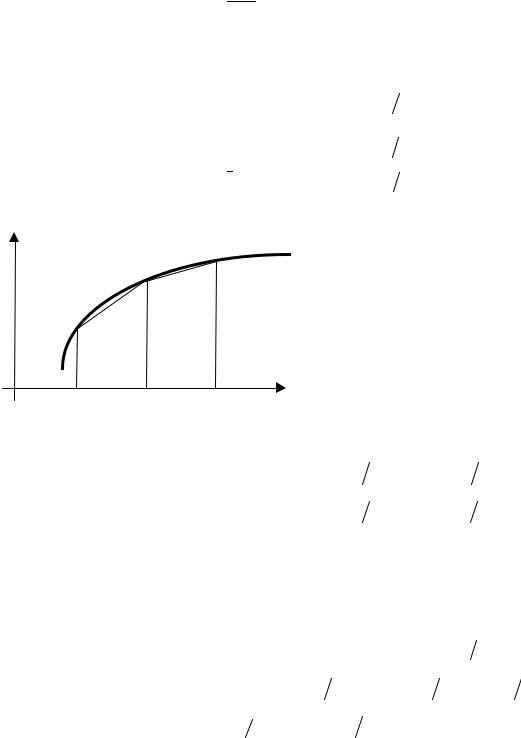
Предполагается, что на заданном отрезке [a,b] введена сеточная область
Ωm = {x0 = a, xi = a + ih, i = 0,m} с шагом h = (b − a)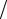 m . В произвольном узле этой области приближенное значение первой производной функции f(x) можно представить несколькими способами:
m . В произвольном узле этой области приближенное значение первой производной функции f(x) можно представить несколькими способами:
|
|
|
fi′,x = [f (xi+1 )− f (xi )] h ; |
|
|
|
|
|
|
|
fi′,x = [f (xi )− f (xi−1 )] h ; |
|
|
|
|
|
|
|
fi′,x = [f (xi+1 ) − f (xi−1 )] 2h . |
|
|
|
|
|
|
|
|
|
|
|
|
Эти формулы с различной сте- |
|
|
|
f(xi + h) |
|
пенью точности представляют зна- |
|
|
f(xi) |
|
чение производной в рассматривае- |
|
|
|
|
|
|
f(xi – h) |
|
|
|
|
мой точке xi (рис. 6.1). Для оценки |
|
|
|
|
|
получаемых погрешностей аппрок- |
|
|
|
|
|
|
симации значений |
производных |
|
|
|
|
|
|
разностными аналогами пользуются |
|
|
|
|
x |
|
|
|
|
|
|
разложениями рассматриваемой фун- |
|
|
|
|
|
|
|
xi – h |
xi |
xi + h |
|
|
|
кции в ряды Тейлора вблизи зада- |
|
Рис.6.1. Схемачисленногодифференцирования нной точки xi : |
|
|
|
|
|
|
′ |
′′ |
|
2 |
′′′ |
3 |
|
4 |
|
|
f (xi+1 ) = f (xi )+ fx (xi )h + |
fxx (xi )h |
2 + fxxx (xi )h |
6 + O(h |
), |
|
|
|
|
|
|
|
′ |
′′ |
|
2 |
′′′ |
3 |
|
4 |
|
|
f (xi−1 ) = f (xi )− fx (xi )h + |
fxx (xi )h |
2 − fxxx (xi )h |
6 + O(h |
). |
|
|
|
|
|
Погрешность аппроксимации первой производной |
|
f ′(xi ) величиной fi′,x |
определяется отклонением действительного значения производной от ее приближенного значения,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψi = fx′(xi )− |
fi′,x = fx′(xi ) − [f (xi+1 ) − f (xi )] h = |
|
′ |
′ |
|
′′ |
|
2 |
+ |
′′′ |
|
|
6 + O(h |
|
)] h = |
= fx |
(xi ) − [fx (xi )h + |
fxx (xi )h |
2 |
fxxx (xi )h |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
′′′ |
|
|
|
6 + O(h |
|
)= O(h). |
|
|
|
= − fxx (xi )h 2 − fxxx (xi )h |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
134

Полученный результат свидетельствует о том, что погрешность аппрок-
симации первой производной fx′(xi ) выражением fi′,x определяется величиной, пропорциональной шагу h сетки Ωm при условии ограниченности второй про-
изводной |
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом случае говорят, что имеет |
fxx (xi ) и малости самого шага h. |
место погрешность аппроксимации первого порядка. |
|
|
|
|
Погрешность аппроксимации первой производной |
fx′(xi ) величиной fi′,x |
оценивается выражением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
x |
( i ) |
|
|
i,x |
|
x ( |
|
i ) |
|
|
|
( i ) |
|
|
|
|
( i−1 ) |
|
|
|
ψ |
− |
f ′ |
= |
|
− |
− f |
|
= |
|
|
= f ′ |
x |
|
f ′ |
x |
f |
x |
x |
h |
|
′ |
|
|
′ |
|
|
|
′′ |
|
|
|
|
|
|
′′′ |
|
|
|
|
6 + O(h |
|
)] h = |
|
= fx (xi ) − [fx (xi )h |
− fxx (xi )h |
2 |
2 + fxxx (xi )h |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
′′′ |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
= fxx (xi )h 2 − fxxx (xi )h |
6 |
+ O(h |
)= O(h). |
|
|
|
|
|
|
|
|
|
В этом случае погрешность аппроксимации также имеет первый порядок. Аналогично выполняется оценка погрешности аппроксимации первой произ-
водной fx′(xi ) величиной |
|
|
|
|
|
|
|
|
|
|
fi′,x : |
|
|
|
|
|
|
ψi = fx′(xi )− f |
i′,x = fx′(xi )− [f (xi+1 )− f (xi−1 )] 2h = |
′ |
|
|
|
′ |
(xi )h + |
′′′ |
|
3 + O(h |
|
)] 2h = |
= fx (xi ) − [2 fx |
fxxx (xi )h |
3 |
4 |
|
|
|
|
|
|
|
|
|
=− f ′′′ (x )h2 6 + O(h3 )= O(h2 ).
xxxi
Впоследнем случае получен второй порядок погрешности аппроксимации. Это означает, что из трех выражений для аппроксимации первой производной последний вариант обеспечивает наименьшую погрешность. В любом из рассмотренных случаев приближение производной ее разностным аналогом тем точнее, чем меньше шаг h выбранной сетки. Вместе с тем следует иметь
ввиду, что уменьшение шага h приводит к возрастанию погрешности вычислений. В самом деле, пусть вместо точных значений f (xi ) и f (xi−1 ) вследствие
ошибок округления получены значения f (xi )+ δi и |
f (xi−1 ) + δi−1 . Аппроксима- |
ция производной |
|
|
|
|
|
|
fi′,x =[f (xi )+ δi − f (xi−1 )− δi−1 ] h =[f (xi )− f (xi−1 )] h + (δi − δi−1 )/ h |
вычисляется |
также с ошибкой δ = (δi − δi−1 ) h . |
При известных оценках |
|
δi |
|
< , |
|
δi−1 |
|
< |
полная погрешность может быть оценена неравенством |
|
|
|
|
δ < 2  h → ∞, h → 0.
h → ∞, h → 0.

Очевидно, следует потребовать, чтобы погрешность округления не превышала погрешности аппроксимации при записи разностного аналога, то есть
2 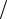 h ≤ M 2h
h ≤ M 2h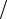 2 ,
2 ,
где
M 2 = max[ ] fxx′′(x)
x a,b
– чёбышевская оценка второй производной заданной функции f(x) на отрезке [a,b]. Отсюда следует
h ≥ 2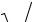 M 2 .
M 2 .
6.2. Использование аппроксимации общего вида
В произвольном узле xi сеточной области Ωm приближенное значение первой производной функции f(x) можно представить в виде
fx′(xi )≈ fi′,x = αf (xi−1 )+ βf (xi ) + γf (xi+1 ),
где α, β, γ – произвольные постоянные величины. Погрешность такого представления производной оценивается разностью
ψi = fx′(xi )− fi′,x = fx′(xi ) − [αf (xi−1 )+ βf (xi ) + γf (xi+1 )].
Используя разложения заданной функции f (x) в ряды Тейлора вблизи точки xi, погрешность аппроксимации первой производной fx′(xi ) можно оценить выражением
|
|
|
ψi = fx′(xi )− fi′,x = |
|
|
|
|
|
|
|
|
|
|
′ |
|
′ |
′′ |
(xi )h |
2 |
/ 2 |
+ |
′′′ |
|
3 |
/ 6 |
+ O (h |
4 |
|
|
− |
fx |
(xi ) − α f (xi ) + |
fx |
(xi )h + fxx |
|
fxxx (xi )h |
|
|
) |
−β[f (xi )]− γ[f (xi )− |
′ |
′′ |
)h |
|
2 |
′′′ |
(xi |
)h |
|
6 + O(h |
|
)], |
fx (xi )h + |
fxx (xi |
2 |
− fxxx |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ипосле приведения подобных слагаемых погрешность аппроксимации равна
ψi = −f (xi )(α+β+γ)+ fx′(xi )(1−αh +γh)− fxx′′(xi )h2 (α+γ)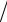 2 +
2 +
+f ′′′ (x )h3 (− α + γ) 6 − O(h4 )(α + γ).
xxxi
Для получения наименьшей погрешности (наивысшей степени шага h) требуется выполнение соотношений
α+β+ γ = 0;
1−αh + γh = 0;
α+ γ = 0.
Отсюда получается, что α =1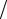 2h, β = 0, γ = −1
2h, β = 0, γ = −1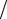 2h , то есть
2h , то есть

fx′(xi )≈ fi′,x = [f (xi+1 ) − f (xi−1 )] 2h . |
|
|
|
(6.1) |
После подстановки найденных значений α, β и γ погрешность аппрокси- |
мации определяется выражением |
|
|
|
|
|
|
|
′′′ |
|
(γ −α) 6 |
−O(h |
|
′′′ |
|
6 =O(h |
|
) |
ψi = fxxx (xi )h |
3 |
4 |
)= − fxxx (xi )h |
2 |
2 |
|
|
|
|
|
|
и не превышает O(h2).
6.3. Применение интерполяционных формул
Для получения приближенного значения производной могут использоваться рассмотренные ранее способы аппроксимации функции полиномами Ньютона (Лагранжа). Идея заключается в замене вблизи заданной точки xi сложной функции, значение производной для которой требуется вычислить, полиномом, для которого и определяется в дальнейшем значение производной. В частности,
для трех точек xi−1, xi , xi+1 |
полином Лагранжа имеет вид |
|
|
|
L (x)= |
(x − xi+1 )(x − xi )f (xi−1 ) |
+ (x − xi−1 )(x − xi+1 )f (xi ) + |
(x − xi−1 )(x − xi )f (xi+1 ) |
= |
2 |
(xi−1 − xi+1 )(xi−1 − xi ) |
(xi − xi−1 )(xi − xi+1 ) |
|
(xi+1 − xi−1 )(xi+1 − xi |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
= (x − xi+1 )(x − xi ) f (xi−1 )− |
(x − xi−1 )(x − xi+1 ) f (xi )+ (x − xi−1 )(x − xi ) f (xi+1 ). |
|
|
hi (hi + hi+1 ) |
|
|
hi hi+1 |
|
|
hi+1 (hi + hi+1 ) |
|
|
|
Определяются первая, |
|
|
|
|
|
|
|
|
|
′ |
|
2x − xi − xi+1 |
|
|
2x − xi−1 − xi |
+1 |
|
|
2x − xi−1 − xi |
|
|
|
L2,x (x)= |
|
f (xi−1 )− |
|
|
f (xi )+ |
|
|
f (xi+1 ) |
, |
|
hi (hi + hi+1 ) |
hi hi+1 |
|
|
hi+1 (hi + hi+1 ) |
|
|
|
|
|
|
|
|
|
|
|
и вторая,
L2′′,xx (x) = 2 f (xi−1 )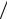 hi (hi + hi+1 ) − 2 f (xi )
hi (hi + hi+1 ) − 2 f (xi )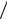 hi hi+1 + 2 f (xi+1 )
hi hi+1 + 2 f (xi+1 )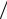 hi+1 (hi + hi+1 ),
hi+1 (hi + hi+1 ),
производные построенного полинома Лагранжа. Для заданной точки xi значение первой производной определяется выражением
L2′(xi ) = −hi+1 f (xi−1 )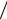 hi (hi + hi+1 )+ (hi+1 − hi )f (xi )
hi (hi + hi+1 )+ (hi+1 − hi )f (xi )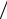 hi hi+1 + hi f (xi+1 )
hi hi+1 + hi f (xi+1 ) hi+1 (hi + hi+1 )
hi+1 (hi + hi+1 )
и от переменной x не зависит. В частном случае постоянного шага сетки hi = hi+1 = h первая и вторая производные принимают значения
L2′,x (xi )= − f (xi−1 ) 2h + f (xi+1 )
2h + f (xi+1 ) 2h = [f (xi+1 )− f (xi−1 )] 2h = fi′,x , L2′′,x (xi )= 2 f (xi−1 )
2h = [f (xi+1 )− f (xi−1 )] 2h = fi′,x , L2′′,x (xi )= 2 f (xi−1 ) 2h2 − 2 f (xi )
2h2 − 2 f (xi ) h2 + 2 f (xi+1 )
h2 + 2 f (xi+1 ) 2h2 =
2h2 =
= [f (xi−1 )− 2 f (xi )+ f (xi+1 )] h2 = fi′,′x .
h2 = fi′,′x .
Контрольные вопросы и задания
6.1.Укажите принципы построения аппроксимации производных функции.
6.2.Определите понятия погрешность аппроксимации, порядок аппрокси-
мации.
6.3.Опишите способ оценки точности аппроксимации производной разностным аналогом.
6.4.Как используются интерполяционные полиномы для построения аппроксимаций производных?
6.5.Установите зависимость степени интерполяционного полинома от порядка аппроксимируемой производной.
6.6.Определите погрешность полученной аппроксимации второй произ-
водной.
6.7.Запишите самостоятельно выражение для аппроксимации смешанной производной ∂2 f (x, y)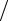 ∂x∂y и оцените погрешность аппроксимации.
∂x∂y и оцените погрешность аппроксимации.
138
7. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Постановка задачи: на отрезке [a,b] задана функция f (x). Определить зна-
чение определенного интеграла |
|
|
I = ∫b |
f (x)dx . |
(7.1) |
a |
|
|
Подынтегральная функция аппроксимируется разложением |
|
n |
|
|
f (x) ≈ ∑ f (xi )ϕi (x), |
(7.2) |
i=0 |
|
отрезка [a, b]; |
где f (xi ) – значения заданной функции в некоторых точках xi |
ϕi (x) – система линейно-независимых функций. Если в качестве ϕi (x) исполь- |
зовать степенные функции xi , то (7.2) – аппроксимация функции |
f (x) полино- |
мом Ньютона (Лагранжа). Подстановка разложения (7.2) в формулу (7.1) приводит к выражению
b |
n |
b |
n |
|
I = ∫ f (x)dx ≈ ∑ f (xi )∫ϕi (x)dx =∑Ci f (xi ), |
(7.3) |
a |
i=0 |
a |
i=0 |
|
где
Ci = ∫b ϕi (x)dx, i = 0,n
a
– весовые коэффициенты. Выражение (7.3) носит название квадратурной фор-
n
мулы интерполяционного типа; ∑Ci f (xi ) – квадратурная сумма.
i=0
Поскольку аппроксимация произвольной функции f (x) связана с опреде-
ленными сложностями (сходимость процесса, наличие погрешности), обычно используется следующий подход. Весь интервал интегрирования [a,b] аппроксимируется разностной сеткой
Ωm = {x0 = a; xk = a + kh; k = 0,m}, h = (b − a) m .
m .
Cвойство аддитивности операции интегрования позволяет представить выражение (7.1) в виде
b |
m |
xk |
I = ∫ f (x)dx = ∑ |
∫ f (x)dx . |
a |
k=1 xk −1 |
139

На каждом из сегментов [xk−1, xk ], k =1,m , проще и удобнее строить и оце-
нивать квадратурные формулы. Погрешность формул интегрирования на произвольном сегменте [xk−1, xk ] определяется как разность между точным значе-
нием интеграла и квадратурной суммой:
xk |
n |
ψk = ∫ f (x)dx − ∑Cik f (xi ). |
xk −1 |
i=0 |
Погрешность численного интегрирования на всем интервале [a,b]
k=1
7.1. Формула прямоугольников
Рассматривается случай, когда в разложении (7.2) удерживается лишь одно слагаемое, содержащее функцию ϕ0 = 1. Весовой коэффициент равен
xk
C0k = ∫ϕ0 dx = h,
xk −1
и на сегменте [xk−1 , xk ] интеграл заменяется выражением
x |
|
|
∫k |
f (x)dx ≈ f (xk −1/ 2 )h . |
(7.5) |
xk −1
Это означает замену интеграла на указанном сегменте площадью прямоугольника с основанием h и высотой, равной значению функции в середине основания прямоугольника (рис. 7.1, б).
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk– |
1 |
xk |
|
xk–1 xk–1/2 xk |
|
|
xk–1 |
|
xk |
|
|
|
|
|
|
а |
|
|
|
|
б |
|
|
|
|
в |
Рис. 7.1. Схема численного интегрирования методом прямоугольников с «левой» (а), «центральной» (б) и «правой» (в) точками


 m . В произвольном узле этой области приближенное значение первой производной функции f(x) можно представить несколькими способами:
m . В произвольном узле этой области приближенное значение первой производной функции f(x) можно представить несколькими способами:


 ∂x∂y и оцените погрешность аппроксимации.
∂x∂y и оцените погрешность аппроксимации.
 m .
m .


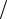
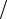 2 ,
2 ,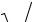 M
M 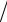
 2
2 2
2 h
h h
h h
h

 h
h
 h
h