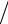Приближение произвольной функции f(x) вблизи xk −1/ 2 описывается фор-
|
мулой Тейлора |
|
|
|
|
|
|
|
|
|
f (x) = f (xk−1/ 2 )+ fx (xk−1/ 2 )(x − xk−1/ 2 ) + fxx (ξ)(x − xk−1/ 2 ) 2, ξ [xk−1, xk ]. |
|
|
′ |
|
|
|
′′ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Погрешность вычисления интеграла на сегменте |
[xk−1, xk ] определяется |
|
выражением: |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψk = ∫k |
f (x)dx − f (xk −1/ 2 )h = |
|
|
|
xk |
xk −1 |
|
|
|
|
|
|
2]dx − f (xk−1/ 2 )h = |
|
(xk −1/ 2 )(x − xk |
−1/ 2 )+ fxx (ξ)(x − xk−1/ 2 ) |
|
= ∫[f (xk−1/ 2 ) + fx |
|
′ |
|
|
|
′′ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
xk |
|
|
|
|
|
= f (xk−1/ 2 )h + fx (xk−1/ 2 )(x − xk−1/ 2 ) |
|
|
|
|
|
|
|
|
2 + fxx (ξ)(x − xk −1/ 2 ) 2dx − f (xk−1/ 2 )h = |
|
′ |
2 |
xk |
∫ |
|
′′ |
|
2 |
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
x
= 1 ∫k fxx′′(ξ)(x − xk−1/ 2 )2 dx .
2 xk −1
Полученное выражение позволяет оценить погрешность
|
ψ |
|
|
≤ |
1 |
|
xk |
f ′′(ξ)(x − x |
|
|
)2 dx |
≤ |
1 |
|
|
max |
|
f ′′(x) |
|
xk (x − x |
|
)2 dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
2 |
|
∫ |
xx |
|
k −1/ 2 |
|
|
2 x [xk −1 ,xk ] |
|
xx |
|
∫ |
k −1/ 2 |
(7.6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
|
|
= M 2,k (x − xk−1/ 2 )3 6 xk |
|
|
|
= M 2,k h3 24 = O(h3 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
f ′′(x) |
|
|
|
|
|
|
|
|
Здесь обозначено: |
M |
|
= max |
|
|
|
|
. Формула (7.6) показывает, что при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,k |
x [xk −1 ,xk |
] |
|
xx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ограниченности второй производной заданной функции на рассматриваемом сегменте погрешность формулы прямоугольников имеет третий порядок. Для всего отрезка интегрирования [a,b] получается:
|
|
|
m |
|
|
|
m |
(mh)h2 24 = M 2h2 |
(b − a) 24, |
|
|
Ψ ≤ ∑ ψk |
|
≤ h3 24∑M 2,k ≤ M 2 |
(7.7) |
|
|
|
|
|
k=1 |
|
|
|
k =1 |
|
|
|
где M |
|
= max |
|
f |
′′ |
(x) |
|
. Иными словами, для всего интервала [a,b] погрешность |
|
|
|
|
|
2 |
x [a,b] |
|
xx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
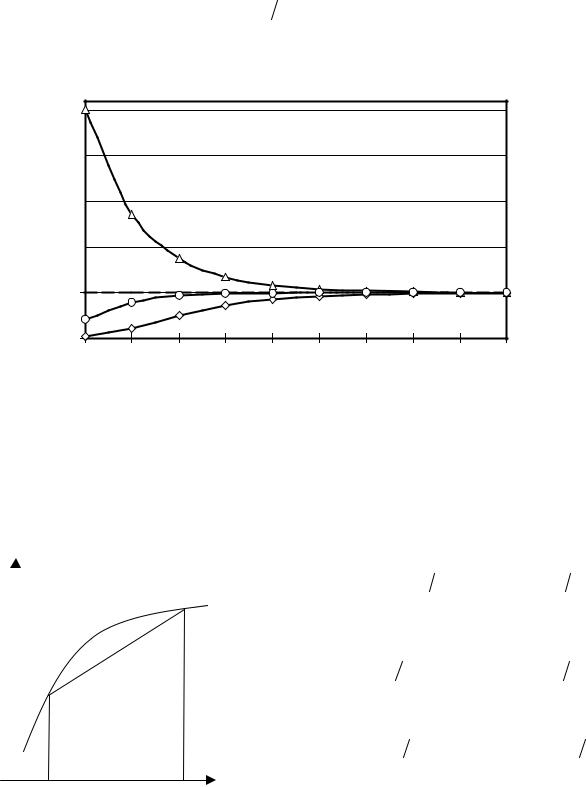
рассмотренного способа интегрирования имеет второй порядок. Так же проверяется часто применяемая на практике формула интегрирования
x∫k f (x)dx ≈ f (xk −1 )h ,
xk −1
с использованием «левой» точки сегмента [xk−1, xk ], геометрический смысл ко-
торой пояснен на рисунке 7.1, а. Оценка погрешности интегрирования на этом сегменте приводит к формуле
x
ψk = fx′(xk−1 )h2 2 + 1 ∫k fxx′′(ξ)(x − xk −1 )2 dx ,
2 xk −1
|
|
|
|
ψk |
|
= O(h2 ). |
|
|
|
|
|
|
|
|
|
|
|
Для всего отрезка [a,b] погрешность интегрирования составляет |
|
Ψ |
|
≤ M1h(b − a) 2, M1 = max |
|
′ |
|
. |
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
|
x [a,b] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рис. 7.2 показана сходимость процесса приближенного вычисления определенного интеграла с помощью формул метода прямоугольников с «центральной», «левой» и «правой» (рис. 7.1, в) точками
5 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
1024 m |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
10
Рис. 7.2. Значения интеграла ∫e−x dx , вычисленные точно ( – – – –),
0
по формулам метода прямоугольников с «центральной» (–ο–), «левой» (– –) и «правой» (–◊–) точками на сетках Ωm
7.2. Формула трапеций
На сегменте [xk−1, xk ] функция f(x) описывается линейной зависимостью
(рис. 7.3):
|
|
|
f (x) ≈(xk − x)f (xk−1 ) h + (x − xk−1 )f (xk ) h . |
|
|
|
|
|
|
Это означает, что в разложении (7.2) |
|
|
|
удерживаются две функции |
|
|
|
ϕ0 (x) = (xk − x) h , |
ϕ1 (x) = (x − xk−1 ) h . |
|
|
|
Весовые коэффициенты равны |
|
|
|
x |
x |
|
|
x |
C0k = ∫k ϕ0 (x)dx = h 2 , C1k = ∫k ϕ1 (x)dx = h 2. |
|
|
xk −1 |
xk −1 |
|
xk–1 |
xk |
Отсюда вытекает формула метода тра- |
|
Рис. 7.3. Схемачисленного |
пеций (см. рис. 7.3): |
|
интегрированияметодомтрапеций

x |
f (x)dx ≈ f (xk−1 )h 2 + f (xk )h 2 = [f (xk−1 )+ f (xk )]h 2. |
|
∫k |
(7.8) |
xk −1 |
|
|
|
|
|
|
Формулы Тейлора разложения функции f(x) возле точки x |
|
f (xk −1 )= f (x) + fx (x)(xk−1 |
− x)+ fxx (ξ)(xk−1 − x) |
|
2, ξ [xk−1, xk ], |
|
|
′ |
′′ |
|
2 |
|
|
|
f (xk ) = f (x)+ fx (x)(xk |
− x)+ fxx (ζ)(xk − x) |
|
2, ζ [xk−1 , xk ]. |
|
|
′ |
′′ |
2 |
|
|
|
|
|
|
|
|
|
|
|
Позволяют оценить погрешность представления (7.8) на сегменте [xk−1, xk ]:
|
x |
|
|
|
ψk = ∫k [f (x) − ϕ0 (x) f (xk−1 ) − ϕ1 (x)f (xk−1 )]dx = |
|
|
|
xk −1 |
|
|
|
x |
|
|
|
|
= ∫k [f (x) − (xk − x)f (xk−1 ) h − (x − xk −1 )f (xk ) h]dx = |
|
xk −1 |
|
|
|
|
xk |
− x)(f (x) + fx (x)(xk−1 |
− x)+ fxx (ξ)(xk−1 − x) |
2) h − |
= ∫[f (x) − (xk |
|
′ |
′′ |
2 |
|
|
|
|
|
xk −1 |
|
|
|
]dx = |
−(x − xk −1 )( f (x) + fx′(x)(xk − x) + fxx′′ (ξ)(xk − x)2 / 2)/ h |
xk
= ∫ f (x)[1 − (xk − x)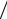 h − (x − xk −1 )
h − (x − xk −1 )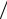 h]dx −
h]dx −
xk −1
xk
− ∫ fx′(x)[(xk − x)(xk−1 − x)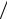 h + (xk − x)(x − xk−1 )
h + (xk − x)(x − xk−1 )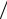 h]dx −
h]dx −
xk −1
− x∫k [fxx′′(ξ)(xk−1 − x)2 (xk − x)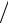 2h + fxx′′(ζ)(xk − x)2 (x − xk−1 )
2h + fxx′′(ζ)(xk − x)2 (x − xk−1 )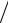 2h]dx .
2h]dx .
xk −1
В силу того, что
1 − (xk − x)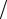 h − (x − xk−1 )
h − (x − xk−1 )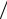 h = 0 ,
h = 0 ,
(xk − x)(xk −1 − x)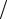 h + (xk − x)(x − xk−1 )
h + (xk − x)(x − xk−1 )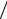 h = 0 ,
h = 0 ,
вычисляемая погрешность определяется выражением
|
|
|
|
xk |
|
|
|
|
|
|
2h]dx . |
ψk = − ∫[fxx (ξ)(xk−1 − x) (xk − x) 2h + fxx (ζ)(xk − x) (x − xk−1 ) |
|
|
|
|
|
′′ |
2 |
|
′′ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
Отсюда следует оценка погрешности: |
|
|
|
|
|
1 |
|
|
xk |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
ψk |
≤ |
|
|
max |
′′ |
∫[(xk−1 |
− x) |
(xk − x) + (xk − x) (x − xk−1 )]dx ≤ |
|
|
|
|
|
|
fxx (x) |
|
|
|
|
2h x [xk −1 ,xk ] |
|
xk −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 2,k |
xk |
|
2 |
|
xk |
|
2 |
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
|
− xk |
|
|
= |
|
|
|
|
|
2h |
∫(xk−1 |
− x) (xk |
− x)dx + ∫(xk − x) (x |
−1 )dx |
|
|
|
|
|
|
|
x |
k −1 |
|
|
|
x |
k |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 2,k |
xk |
|
2 |
|
xk |
|
2 |
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
|
− xk |
|
|
= |
|
|
|
|
|
2h |
∫(xk−1 |
− x) (xk |
− x)dx + ∫(xk − x) (x |
−1 )dx |
|
|
|
|
|
|
|
x |
k −1 |
|
|
|
x |
k |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 2,k |
|
xk |
|
2 |
xk |
3 |
|
xk |
2 |
xk |
3 |
|
|
= |
2h |
h ∫(xk−1 |
− x) dx |
+ ∫(xk−1 |
− x) |
dx + h ∫ (xk − x) |
dx − ∫(xk |
− x) dx |
|
= |
|
|
x |
k |
−1 |
|
|
x |
k −1 |
|
|
|
x |
k −1 |
|
|
x |
k −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
|
|
= M 2,k {h(x − xk−1 )3 3 − (x − xk−1 )4 4 + (x − xk )4 4 − h(x − xk )3 3}xk −1 2h = |
|
|
|
|
|
|
= M 2,k {h4 3 − h4 4 − h4 4 + h4 3} 2h = M 2,k h3 12. |
|
|
|
Для всего отрезка интегрирования [a,b] погрешность |
|
|
|
|
|
|
|
|
m |
|
|
|
m |
|
12 ≤ M 2 (mh)h2 |
12 = M 2h2 (b − a) 12 , |
|
|
|
|
Ψ ≤ ∑ ψk ≤ h3 ∑M 2,k |
|
|
(7.9) |
|
|
k =1 |
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
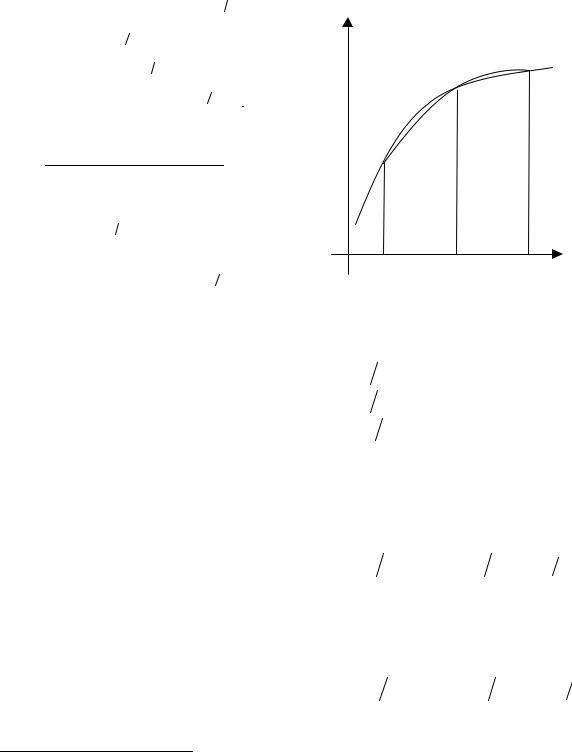
имеет второй порядок. На рис. 7.4 показана сходимость приближенного зна- |
чения заданного интеграла, полученного с помощью формул метода трапе- |
ций. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1024 m |
|
|
|
|
2 |
|
|
4 |
|
8 |
|
16 |
32 |
64 |
|
128 |
256 |
512 |
|
|
10
Рис. 7.4. Значения интеграла ∫e−x dx , вычисленные точно ( – – – – )
0
и по формуле метода трапеций (–ο– ) на сетках Ωm
7.3. Формула Симпсона1
На сегменте [xk−1, xk ] функция f(x) аппроксимируется полиномом Лагранжа (рис. 7.5). Для узлов xk−1, xk−1 2 , xk полином второй степени имеет вид
L (x) = |
(x − xk−1 2 )(x − xk )f (xk−1 ) |
+ |
|
2 |
(xk−1 |
− xk−1 2 )(xk−1 |
− xk ) |
|
|
|
+ (x − xk−1 )(x − xk )f (xk−1 2 )+
(xk−1 2 − xk−1 )(xk−1
2 − xk−1 )(xk−1 2 − xk )
2 − xk )
+ (x − xk−1 )(x − xk−1 2 )f (xk ) = (xk − xk−1 )(xk − xk−1
2 )f (xk ) = (xk − xk−1 )(xk − xk−1 2 )
2 )
|
|
|
= |
|
|
2 |
|
|
[(x − xk−1 2 )(x − xk )f (xk−1 ) − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2(x − xk−1 )(x − xk )f (xk−1 2 )+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk–1 |
|
|
xk–1/2 |
|
xk |
|
|
|
|
|
|
|
|
|
|
+(x − xk −1 )(x − xk −1/ 2 ) f (xk )]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.5. Схема численного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интегрирования методом Симпсона |
Это означает, что в разложении (7.2) оставлены три функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ0 (x)= 2(x − xk−1/ 2 )(x − xk |
) h2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
(x) = − 4(x − x |
k−1 |
)(x − x |
k |
) h2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ2 |
(x)= 2(x − xk −1 )(x − xk−1/ 2 ) h2 . |
|
|
|
|
|
|
|
Для определения коэффициентов C k , C k , C k |
|
вычисляются интегралы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
C0k = |
|
xk |
ϕ0 (x)dx = |
2 |
|
xk |
(x − xk−1/ 2 )(x − xk )dx = |
2 |
xk (x − xk + xk − xk−1/ 2 )(x − xk )dx = |
|
∫ |
|
h2 |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
xk |
2 |
|
|
|
|
h xk |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
xk |
|
|
|
= |
|
|
|
|
|
|
|
∫ (x − xk ) |
|
dx |
+ |
∫ |
(x − xk |
)dx |
= |
|
|
|
|
[(x − xk ) 3 + h(x − xk ) |
4]xk −1 = h 6; |
|
|
h |
2 |
|
|
|
h |
2 |
|
|
|
|
|
|
|
x |
|
− |
|
|
|
|
|
|
|
2 x |
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
k |
1 |
|
|
|
|
|
|
xk |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
|
|
C k = |
|
|
ϕ (x)dx = − |
|
4 |
|
(x − x )(x − x )dx = − |
4 |
|
(x − x + x − x )(x − x )dx = |
|
|
∫ |
h2 |
∫ |
h2 |
|
∫ |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
k−1 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
k |
k |
|
k−1 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
|
|
|
4 |
|
xk |
2 |
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
xk |
|
|
|
= − |
|
|
|
|
|
∫(x − xk |
) dx + h ∫(x − xk )dx = − |
|
|
|
|
[(x − xk ) 3 |
+ h(x − xk ) |
2]xk −1 = 2h 3 |
; |
h |
2 |
|
|
h |
2 |
|
|
|
|
x |
− |
|
|
|
|
|
|
|
x − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
1 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 Симпсон Томас [20.8.1710 – 14.5.1761] – английский математик. С 1713 года был профессором Вулиджской военной академии, в 1746 году был избран членом Лондонского королевского общества.
Рассматриваемый метод интегрирования иногда называют также методом парабол.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
= f (xk−1/ 2 )h + fxx (xk−1/ 2 )h |
|
|
|
24 + ∫ fxxxx (ς)(x − xk −1/ 2 ) dx 24 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
iv |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
k |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− h[6 f (xk−1/ 2 ) + |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
iv |
|
|
|
|
iv |
|
|
|
|
|
fxx (xk−1/ 2 )h |
|
4 + h |
|
|
|
|
|
|
|
|
|
6 = |
|
|
|
|
(fxxxx (ζ) − |
fxxxx (ξ)) 384] |
|
|
|
|
x |
fxxxxiv (ς)(x − xk−1/ 2 )4 dx 24 − h5 [fxxxxiv (ζ)− fxxxxiv (ξ)] 2304 . |
|
= ∫k |
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценивается модуль погрешности на сегменте [xk−1 , xk ]: |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψk |
|
|
≤ |
|
∫k |
|
fxxxxiv |
(ς)(x − xk−1/ 2 )4 dx 24 |
+ h5 |
|
fxxxxiv (ζ)− fxxxxiv (ξ) |
2304 ≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ |
max |
|
|
f iv |
(x) |
|
xk |
(x − x |
k−1/ 2 |
)4 dx 24 + |
|
max |
f iv |
(x) h5 |
1152 = |
|
|
|
|
|
x [xk −1 ,xk |
] |
|
xxxx |
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [xk −1 ,xk ] |
|
xxxx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk −1 |
(x) |
|
{h5 1920 + h5 |
1152}= M |
|
|
|
|
|
|
|
|
= |
|
|
max |
|
f iv |
|
|
4,k |
h5 720 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [xk −1 ,xk ] |
|
|
|
xxxx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для всего отрезка [a,b] интегрирования погрешность |
|
|
|
m |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(mh)h4 |
720 = M 4h4 (b − a) |
|
|
Ψ = ∑ ψk ≤ h5 ∑M 4,k |
|
720 ≤ M 4 |
720 |
(7.11) |
k=1 |
|
|
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеет четвертый порядок. В формуле (7.11) использованы обозначения: |
|
|
|
|
|
|
|
|
|
M |
4,k |
= |
max |
|
f iv |
|
(x) |
|
, |
|
M |
4 |
= max |
|
f iv |
(x) |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [xk −1 ,xk ] |
|
xxxx |
|
|
|
|
|
|
|
|
x [a,b] |
|
|
xxxx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рис. 7.6 отображена сходимость приближенного значения определенного интеграла, полученного с помощью формул метода Симпсона.
1,15 |
|
|
|
|
|
|
|
|
|
1,11 |
|
|
|
|
|
|
|
|
|
1,07 |
|
|
|
|
|
|
|
|
|
1,03 |
|
|
|
|
|
|
|
|
|
0,99 |
|
|
|
|
|
|
|
|
|
0,95 |
|
|
|
|
|
|
|
|
1024 m |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
10
Рис. 7.6. Значенияинтеграла ∫e−x dx , вычисленныеточно
0
( – – – – ) ипоформулеметодаСимпсона( –ο– ) насеткахΩm
7.4. Формула Эйлера1
При исследовании численного интегрирования методом трапеций получена формула для вычисления погрешности на отрезке [xk−1 , xk ]:
xk |
− x) (xk − x) 2h + fxx (ζ)(xk − x) (x − xk−1 ) 2h]dx . |
ψk = − ∫[fxx (ξ)(xk−1 |
′′ |
2 |
′′ |
2 |
|
|
xk −1 |
|
|
|
Предполагается, что |
ξ = ζ = xk −1/ 2 , |
то есть равны координате в середине |
указанного сегмента. Тогда может быть приближенно вычислена погрешность интегрирования:
xk |
|
|
|
|
|
xk |
|
|
|
(xk−1/ 2 ) 2h = |
ψk ≈ − ∫(xk−1 − x)2 |
(xk − x)dx + ∫(xk − x)2 |
(x − xk −1 )dx fxx′′ |
x |
k −1 |
|
|
|
|
|
x |
k −1 |
|
|
|
(7.12) |
|
|
|
|
|
|
|
|
|
|
|
= − [h |
3 |
12 |
+ h |
3 |
|
′′ |
|
|
3 |
′′ |
|
|
|
|
12]fxx (xk −1/ 2 ) 2h = −h |
|
fxx (xk −1/ 2 ) 12. |
Учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
f (x)dx −h[f (xk−1 ) + f (xk )] 2 , |
|
|
|
|
|
ψk = ∫k |
|
xk −1
можно получить уточненную формулу интегрирования:
x∫k f (x)dx ≈h[f (xk−1 )+ f (xk )]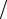 2 − h3 fxx′′(xk−1/ 2 )
2 − h3 fxx′′(xk−1/ 2 )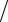 12.
12.
xk −1
Согласно теореме Лагранжа
fxx′′(xk−1/ 2 )h ≈ fx′(xk )− fx′(xk−1 ),
откуда следует формула интегрирования Эйлера:
x |
f (x)dx ≈h[f (xk−1 )+ f (xk )] 2 − h2 [fx′(xk )− fx′(xk−1 )] 12 . |
|
∫k |
(7.13) |
xk −1
Погрешность формулы (7.13) на отрезке [a,b] оценивается формулой, совпадающей с выражением (7.11).
1 Эйлер Леонард [4.4.1707 – 7.9.1783] – математик, механик, физик. В 1720 году поступил в Базельский университет, где получил степень магистра искусств. С 1727 года работал в Петербургской академии наук. В 1741 году занял пост директора класса математики Берлинской академии наук. С 1759 года в течение ряда лет руководил этой академией. В1766 году вернулся в Петербург, где до конца жизни подготовил около 400 научных трудов. Был избран членом Парижской академии наук и Лондонского королевского общества.
148
7.5. Оценка погрешности методом Рунге1
Для получения оценки погрешности рассматривается формула интегрирования методом трапеций. Для сегмента [xk−1, xk ] вводятся обозначения:
xk
Jk = ∫ f (x)dx ,
xk −1
Jh,k = h[f (xk ) + f (xk−1 )] 2.
2.
В соответствии с полученным выражением (7.12) можно записать:
xk |
|
|
|
|
Jk − Jh,k = ∫ f (x)dx − h[f (xk )+ |
f (xk−1 )] 2 = ψk ≈ −h |
3 |
′′ |
, |
|
fxx (xk−1/ 2 ) 12 |
xk −1
или, иначе,
Jk − Jh,k ≈ Ck h3 . |
(7.14) |
Далее шаг уменьшается вдвое и вновь проводится интегрирование на том же сегменте [xk−1, xk ]. Общая погрешность равна
Jk − Jh / 2,k ≈ Ck (h 2)3 + Ck (h 2)3 = Ck h3 4 . |
(7.15) |
Вычитание формулы (7.15) из выражения (7.14) дает:
Jh / 2,k − Jh,k ≈ Ck h3 − Ck h3  4 = Ck 3h3
4 = Ck 3h3  4 .
4 .
Это позволяет определить коэффициент
Ck ≈ 4(Jh / 2,k − Jh,k )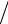 3h3
3h3
и подсчитать погрешность вычисления интегралов:
Jk − Jh,k ≈ 4(Jh / 2,k − J Jk − Jh / 2,k ≈ (Jh / 2,k − J
)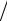 3 , )
3 , )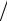 3 .
3 .
Следовательно, зная величины Jh / 2,k и Jh,k , можно получать оценки по-
грешностей при численном нахождении значения интеграла. В более общем случае (для произвольной схемы интегрирования с порядком погрешности p), можно получить следующие выражения:
Jk − Jh,k ≈ Ck h p ,
Jk − Jh / 2,k ≈ 2Ck (h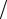 2)p ,
2)p ,
1 Рунге Карл Давид Тольме [30.8.1856 – 3.1.1927] – немецкий физик и математик. В 1876–1877 годах учился в Мюнхенском, в 1878–1880 годах – в Берлинском университете. Работал в Берлине, Ганновере, Геттингене.

Ck ≈ 2 p h− p (Jh / 2,k − Jh,k ) (2 p − 2).
(2 p − 2).
Оценки погрешности принимают вид
Jk − Jh,k ≈ 2 p−1 (Jh / 2,k − Jh,k ) (2 p−1 −1), Jk − Jh / 2,k ≈ (Jh / 2,k − Jh,k )
(2 p−1 −1), Jk − Jh / 2,k ≈ (Jh / 2,k − Jh,k )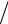 (2 p−1 −1).
(2 p−1 −1).
Приведенные формулы позволяют автоматизировать процесс вычисления интегралов с заданной точностью. Пусть на каждом из отрезков половинное дробление производится до тех пор, пока не выполнится условие
ψk = Jk − Jh / 2,k ≈ (Jh / 2,k − Jh,k )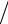 (2 p−1 −1)≤ εh
(2 p−1 −1)≤ εh (b − a), k =1,m .
(b − a), k =1,m .
Тогда общая погрешность интегрирования
|
|
m |
|
|
|
m |
(b − a)= ε. |
J − Jh / 2 |
|
= ∑ |
|
ψk |
|
≤ ε∑h |
|
|
|
|
|
k=1 |
|
|
|
k=1 |
|
Таким образом, вычисления с переменным шагом позволяют проводить численное интегрирование с заданной точностью при наименьших затратах.
7.6. Квадратурные формулы интерполяционного типа
Предполагается, что функция f(x) на всей сеточной области Ωm аппрокси-
мируется полиномом Лагранжа: |
−1 )(x − xk+1 ) … (x − xm ) |
|
|
|
f (xk ). |
|
Lm (x) = ∑ (x − x0 ) … (x − xk |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=0 |
(xk − x0 ) … (xk − xk−1 )(xk − xk+1 ) … (xk − xm ) |
|
|
|
|
|
Сопоставлением полученного выражения с формулой (7.2) определяется |
явный вид для функций ϕk (x): |
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕk (x) = |
(x − x0 ) … (x − xk−1 )(x − xk+1 ) … (x − xm ) |
|
, k = |
|
. |
|
|
0,m |
|
(xk − x0 ) … (xk − xk−1 )(xk − xk+1 ) … (xk − xm ) |
|
|
|
|
|
|
|
|
|
|
Весовые коэффициенты формулы (7.3) определяются явным образом: |
b |
|
b |
(x − x0 ) … (x − xk −1 )(x − xk +1 ) … (x − xm ) |
|
|
|
|
|
|
Ck = ∫ϕk (x)dx = ∫ |
|
|
|
|
|
|
|
|
|
dx . |
(7.16) |
(x |
− x |
) … (x − x |
k −1 |
)(x |
− x |
) … (x − x |
m |
) |
a |
|
a |
k |
0 |
k |
k |
k +1 |
k |
|
|
|
|
|
|
|
Для подсчета погрешности квадратурной формулы интерполяционного |
типа используется оценка погрешности интерполяционного полинома: |
|
|
f (x) − L (x) = f (m+1)(ξ)ω(x) (m +1)!, ξ [a,b], |
|
|
|
|
|
|
|
|
|
|
|
m |
x…x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω(x) = (x − x0 )(x − x1 ) … (x − xm ). |
Погрешность формулы приближенного интегрирования на отрезке [a,b] |
b |
m |
b |
b |
Ψ = ∫ f (x)dx − ∑Ck f (xk ) = ∫[f (x)− Lm (x)]dx = ∫ fx(…mx+1)(ξ)ω(x)dx (m +1)!, |
a |
k=0 |
a |
a |








 2 − h3 fxx′′(xk−1/ 2 )
2 − h3 fxx′′(xk−1/ 2 ) 12.
12.


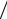 h
h  h
h h
h  h
h
 h
h  h
h  2
2  2
2 




 3 ,
3 ,  3 .
3 .