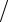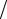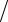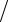Методы вычислительной математики
..pdf

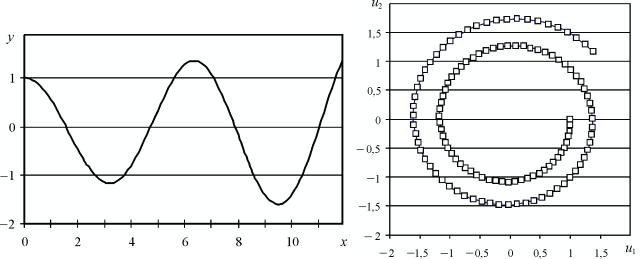
Рис. 8.7. Численное решение методом |
|
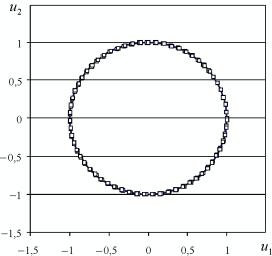
Рис. 8.8. Фазовая диаграмма |
|||
Эйлера уравнения |
y′′ |
+ y = 0 сшагом |
|
||
|
xx |
|
результатов численного решения |
||
интегрирования h = 0,1 |
|||||
|
методом Эйлера уравнения |
||||
|
|
|
y′′ |
||
|
|
|
+ y = 0; шагинтегрированияh = 0,1 |
||
|
|
|
xx |
|
|
8.8.2. Метод Рунге–Кутты для системы дифференциальных уравнений
Рассматривается наиболее распространенная схема четвертого порядка аппроксимации. Вводятся матрицы
|
|
|
f1 (xk ,u1k ,...,unk ) |
|
|
|
|
|
|
|
(xk ,u1k ,...,unk ) |
|
|
{ |
K1 |
= |
f2 |
|
, |
|
} |
|
|
|
|
|
|
|
|
|
........................... |
|
|
|
|
|
|
|
|
|
|
|
|
|
fn (xk ,u1k ,...,unk ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1 (xk |
+ h / 2,u1k |
+ hK11 / 2,...,unk |
+ hK1n |
/ 2) |
|
|
|
|
(xk |
|
|
|
|
|
|
f2 |
+ h / 2,u1k |
+ hK11 / 2,...,unk |
+ hK1n |
/ 2) |
, |
||
{K 2} = |
|
|
|
|
|
|
|
...................................................................... |
|
||||||
|
|
|
|
|
|
|
|
fn (xk |
+ h / 2,u1k |
+ hK11 / 2,...,unk |
+ hK1n |
/ 2) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
185








 2
2 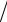
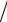
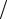 2 . На третьей итерации можно ожидать повышения порядка аппроксимации до третьего, и так далее. Однако следует иметь в виду, что сама исходная схема (8.14) имеет
2 . На третьей итерации можно ожидать повышения порядка аппроксимации до третьего, и так далее. Однако следует иметь в виду, что сама исходная схема (8.14) имеет  6
6