Методы вычислительной математики

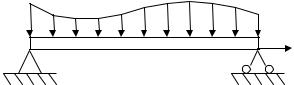
9. ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

В отличие от задачи Коши, в граничных задачах условия для определения постоянных интегрирования задаются в нескольких различных точках отрезка, на котором строится решение дифференциальной задачи. В качестве примера рассматривается ряд постановок таких задач.

Механическое движение точки вдоль прямой описывается уравнением mxtt′′ = Fx (t, x, xt′),

причем известно, что к моменту времени Т точка должна пройти расстояние L. Требуется найти закон движения точки. Очевидно, что условия для нахождения постоянных интегрирования в рассматриваемом случае заданы для разных моментов времени и могут быть записаны так: x(0) = 0, x(T) = L.

Неподвижная горизонтальная балка закреплена на опорах и испытывает действие распределенной по ее длине перерезывающей нагрузки (рис. 9.1). Уравнение изгиба

балки записывается в форме

EIw′xx′ = −M (x),

где Е – модуль упругости материала, I – момент инерции поперечного сечения балки, w(x) – функция, описывающая прогиб балки, М(х) – переменный из-

гибающий момент от действия поперечной нагрузки q(x). Шарнирные закрепления балки на опорах означают, что прогибы в крайних точках равны нулю: w(0) = 0, w(L) = 0.

Температурное поле θ(x) в стержне, теплоизолированном с боковой поверхности, описывается уравнением одномерной теплопроводности:

λθ′xx′ + J (x,θ)= 0 ,

где λ – коэффициент теплопроводности, J(x, θ) – мощность внутренних тепловых источников. Предполагается, что на левом торце стержня поддерживается постоянная температура θ(0) = θ0 (граничное условие первого рода), а на пра-

191

поверхности стрежня в окружающую среду. Иначе последнее условие может быть записано в виде смешанного граничного условия αθ(L)+ λθ′x (L)=αθcp (граничное условие третьего рода).

Поскольку обыкновенное дифференциальное уравнение порядка n можно представить в виде системы n обыкновенных дифференциальных уравнений первого порядка, в общем случае постановка граничной задачи выглядит следующим образом: определить дифференцируемые функции uk (x), удовлетво-

ряющие дифференциальным уравнениям

на отрезке [a, b], причем условия накладываются на функции uk (x) более чем в одной точке этого отрезка,

9.1. Метод пристрелки

Требуется отыскать решение системы двух обыкновенных дифференци-

можно рассматривать как начальные условия для системы дифференциальных уравнений (9.3), то есть вместо граничной задачи сформулирована задача Коши. Решая каким-либо известным способом задачу (9.3) с начальными условиями (9.5), можно найти решения u1 (x; D) и u2 (x; D) как функции парамет-

ра D. Однако при подстановке этих решений во второе граничное условие (9.4)

192

в общем случае не будет получено тождество из-за произвольного выбора па-

можно рассматривать как нелинейное уравнение относительно параметра D

~

и использовать для определения D любой из известных методов поиска корня нелинейного уравнения.

Пример 9.1. Решить задачу теплопроводности для однородного тонкого стержня с теплоизолированной боковой поверхностью:

λθ′xx′ + J (x,θ)= 0

при λ = const, J = const и граничных условиях

αθ(0)λθ′x (0) = αθcp , θ(1) = θ1.

Вводятся обозначения

u1 = θ, u2 = θ′x ,

которые позволяют представить исходное уравнение в виде системы двух обыкновенных дифференциальных уравнений:

u1′, x (x) = u2 (x),

u2′, x (x) = −J / λ

с граничными условиями

что позволяет перейти к задаче Коши,

193

Интегрирование этой системы дает решение

Использование начальных условий

u1 (0) = D, u2 (0)= α(D − θср )λ

позволяет определить постоянные интегрирования

C1 = α(D − θcp )/ λ, C2 = D.

и записать решение задачи в виде

u (x) = −Jx / λ + α(D − θcp )/ λ,

2

Подстановка полученного решения во второе граничное условие u1 (1)= θ1 дает выражение

u1 (1)= −J2λ + α(D − θср )λ + D = θ1

которое можно рассматривать как уравнение относительно произвольного параметра D, что позволяет определить неизвестную величину

9.2. Метод дифференциальной прогонки

Рассматривается система n обыкновенных дифференциальных уравнений

Пусть в точке x1 задано p1 граничных условий, в точке x2 – p2 граничных условий, и так далее. Общее число граничных условий равно числу дифферен-

m

циальных уравнений системы (9.6), то есть ∑ pk = n . Например, для системы

k=1

двух дифференциальных уравнений задача (9.6)–(9.7) представляется в форме

194

Соответствующие матрицы в выражениях (9.6) и (9.7) принимают вид

Основная идея метода дифференциальной прогонки заключается в сведении граничной задачи (9.6), (9.7) к задаче Коши, то есть в сведении граничных условий (9.7), заданных для m разных значений аргумента, к n условиям, заданным для одного значения аргумента. Рассматривается вспомогательное функциональное соотношение

Если предположить, что функциональные матрица [v(x)] и вектор {γ(x)} известны, выражение (9.8) для заданного x = b представляет собой систему алгебраических уравнений

относительно значений u1 (b), u2 (b), …, un (b), которые теперь можно использо-

вать как начальные условия для системы обыкновенных дифференциальных уравнений (9.6).

Выражение (9.8) дифференцируется в предположении, что [v(x)] и {γ(x)} – достаточно гладкие (дифференцируемые) функции,

[v′(x)]T {u(x)}+ [v(x)]T {u′x (x)}= {γ′(x)}.

195

С учетом исходной системы уравнений (9.6) из приведенного соотношения получается

[v′(x)]T {u(x)}+ [v(x)]T ({f (x)}− [A(x)]{u(x)}) ={γ′(x)}, ([v′(x)]T − [v(x)]T [A(x)]){u(x)}={γ′(x)}− [v(x)]T {f (x)}.

Последнее выражение будет справедливо для любых функций {u(x)}, например, при выполнении условий

[v′x (x)]T − [v(x)]T [A(x)]= 0, {γ′x (x)}− [v(x)]T {f (x)}= 0.

Отсюда получается система n × n + n обыкновенных дифференциальных

ничных условий. В (9.10) и (9.11) выбираются подходящие дифференциальные уравнения (таких уравнений будет p1 × p1 + p1 ), для которых с помощью этих

граничных условий можно определить начальные условия, и интегрируются на отрезке [x1, x2]. Это позволит определить значения выбранных функций [v(x)] и {γ(x)} в следующей точке x2. Но в этой точке заданы еще p2 граничных условий исходной задачи, что, в свою очередь, позволяет выбрать еще p2 × p2 + p2

дифференциальных уравнений из систем (9.10), (9.11) и проинтегрировать их вместе с первым набором уравнений на втором участке. Последовательно выполняя эту процедуру для всех отрезков [xk , xk+1 ], k =1,m −1, в конечном итоге

можно получить значения всех функций [v(xm)] и {γ(xm)} для последней точки отрезка xm = b. Наконец, решением системы алгебраических уравнений (9.9)

определяются значения искомых функций {u(b)}, которые можно рассматривать как начальные условия задачи (9.6), то есть фактически производится переход к задаче Коши.

196

рассматриваются две специальные системы функций. Первая система функций {ψk }, k =1,2,…, называемых взвешивающими, удовлетворяет следующим

требованиям:

1) ψk C[a,b], k =1,2,…;

2) ψk , k =1,2,… образуют полную1 на [a, b] систему функции. Согласно [20] полными являются, например, системы функций:

– тригонометрических: 1, cos(nt), sin(nt), n = 1,2, … на отрезке [–π, π];

–полиномиальных: 1, t, t2 , … на любом произвольном отрезке [a, b];

–Эрмита2: Hk (t)e−t22 , k = 0, 1, 2, … на (–∞, ∞),

1 Согласно [17] в гильбертовом пространстве L2 с нормой x = (x, x)12 , порожденной

b

скалярным произведением (x, y) = ∫ x(t)y(t)dt , система элементов {ψk }, k =1,2,… является

a

полной, если не существует отличного от нуля элемента, ортогонального на [a, b] каждому

b

элементу ψk системы. Иначе, из условия ∫ y(t)ψk (t)dt = 0 следует, что y(t) = 0 t [a,b].

a

2Эрмит Шарль [24.12.1822 – 14.1.1901] – французский математик, был иностранным членом-корреспондентом и иностранным почетным членом Петербургской академии наук, членом Парижской академии наук и Лондонского королевского общества, профессором Парижского университета. Выполнил исследования в области классического анализа, алгебры, теории чисел, эллиптических функций, ортогональных многочленов.

3Лагерр Эдмон Никола [9.4.1834 – 13.8.1886] – французский математик, член Парижской академии наук. Основные труды выполнены в области геометрии, теории функций комплексного переменного, ортогональных многочленов.

197

Для второй системы пробных функций ϕk , k = 0,1,2,…, должны выполняться следующие условия:

1) ϕk C[2a,b], k = 0,1,2,…;

2)ϕk являются линейно независимыми на [a, b];

3)ϕ0 удовлетворяет граничным условиям (9.13),

4) ϕk , k = 0,1,2,…, образуют в G замкнутую1 систему функций. Для рассматриваемого случая это означает, что η G отыщется линейная комбинация функций ϕk , приближающая функцию η и ее производные сколь угодно

точно.

Решение задачи (9.12)–(9.13) разыскивается в виде разложения в ряд по пробным функциям ϕk , k = 0,1,2,…,

виям (9.13) при любых значениях коэффициентов ak , k =1,m . В общем случае подстановка выражения (9.14) в уравнение (9.12) не обращает его в тождество:

F(x, ym , ym′ ,x , y′m′,xx )≠ 0

1 Согласно [14] замкнутой является такая система элементов {ϕk }, k = 0,1, 2,..., нор-

мированного пространства G, что любой элемент x G можно сколь угодно точно приблизить конечной линейной комбинацией элементов ϕk . Иными словами, ε > 0 найдутся та-

m

кие скаляры a1 ,a2 , …, an , что имеет место неравенство x − ∑ak ϕk < ε.

k =1

198

тов ak , k =1,m , разложения (9.14) решения исходной задачи по пробным функциям. Полагая все μ j = 0 , получаемое выражение

a

можно рассматривать как систему алгебраических уравнений, в общем случае нелинейных, относительно коэффициентов разложения решения дифференциальной задачи (9.12)–(9.13) в ряд (9.14) по замкнутой системе функций. Благодаря свойству полноты системы функций ψ j , j =1,2,…, условие (9.15) озна-

чает, что при m → ∞ невязка F (x, ym , y′m,x , y′m′,xx )= 0. Но это, в свою очередь,

приводит к тому, что ym → y, то есть разложение (9.14) сходится к реше-

m→∞

нию исходного дифференциального уравнения.

На практике ограничиваются решением конечной системы m алгебраических уравнений (9.15) c m неизвестными. Понятно, что повышение точности получаемого приближенного решения связано с повышением числа m слагаемых, удерживаемых в представлении (9.14).

Пример 9.2. Решить уравнение стационарной теплопроводности

(λθ′x (x))′x + J (x) = 0

для стержня единичной длины, теплоизолированного с боковой поверхности; полагается, что на левом и правом торцах поддерживается заданная температу-

ра θ(0) = θ0 , θ(1)= θ1 ; λ = const, J = const.

Система пробных функций строится на основе полиномов. В качестве «нулевой» выбирается линейная функция ϕ0 (x)= G + Hx. Коэффициенты G и H

разом, ϕ0 (x)= θ0 + (θ1 − θ0 )x.

199

Остальные пробные функции представляются в форме, удовлетворяющей однородным условиям задачи, например:

Понятно, что такое представление является неединственным. Для упрощения принято, что m = 3. Приближенное решение

y3 (x) = ϕ0 (x)+ a1ϕ1 (x)+ a2ϕ2 (x)+ a3ϕ3 (x)

подставляется в исходное дифференциальное уравнение:

F(x,y3 ,y3′,x ,y3′′,xx )= λ[2a1 + a2 (6x − 2) + a3 (12x2 − 6x)]+ J ≠ 0.

В качестве взвешивающих функций выбираются три первые элемента системы тригонометрических функций: 1, cos(t), sin(t).

Вычисляются значения моментов:

μ1 = ∫1 [2a1λ + a2λ(6x − 2)+ a3λ(12x2 − 6x)+ J ] 1dx = λ(2a1 + a2 + a3 )+ J ,

0

μ2 = ∫1 [2a1λ + a2λ(6x − 2)+ a3λ(12x2 − 6x)+ J ]cos(x)dx =

0

= 2a1λsin(1)+ a2λ[6cos(1)+ 4sin(1)− 6]+ a3λ[18cos(1) + 6sin(1) + 6]+ J sin(1),

μ3 = ∫1 [2a1λ+a2λ(6x −2)+a3λ(12x2 −6x)+ J]sin(x)dx =

0

= 2a1λ[1−cos(1)]+a2λ[6sin(1)−4cos(1)−2]+6a3λ[3sin(1)+3cos(1)−4]+ J[1−cos(1)].

Система линейных алгебраических уравнений (9.15) для рассматриваемой задачи принимает вид

Решением этой системы являются коэффициенты a1 = −J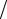2λ, a2 = 0, a3 = 0 ,

позволяющие представить решение в виде

y3 (x) = θ0 + (θ1 − θ0 )x − J (x −1)x 2λ = θ0 + (θ1 − θ0 + J 2λ)x − Jx2 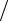2λ.

Полученное решение является точным для поставленной задачи.

200