Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методы вычислительной математики

..pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

3.42 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 4311 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

онно под сплайном понимают интерполяцию табличной функции с помощью отрезков кубического полинома.

4.2.1. Построение кубического сплайна

Пусть на отрезке [a,b] определена сеточная область Ωm с неравноотстоящими узлами a = x0 < x1 <…< xm = b , в которых известны табличные значения

функции f (xk )= fk ,

k =

. Сплайн S(x)

должен удовлетворять следующим

0,m

условиям:

а) на каждом сегменте [xk−1, xk ], k =

является кубическим полиномом;

1,m

′

′′

б) непрерывен на [a,b] вместе с производными Sx (x)

и Sxx (x);

в) совпадает со значениями f (xk ) аппроксимируемой функции в узлах сетки.

Сплайн S(x) на каждом сегменте [xk−1, xk ]отрезка [a,b] строится в виде

Sk (x) = ak + bk (x − xk )+ ck (x − xk )2 2 + dk (x − xk )3 6,

k =

;

(4.8)

1,m

′

′′

Определяются первая Sx (x) и вторая Sxx (x) производные

Sk′, x (x) = bk + ck (x − xk )+ dk (x − xk )2 2 ,

Sk′′,xx (x) = ck + dk (x − xk ),

которые для двух «соседних» сплайнов Sk (x) и Sk+1 (x) в общей точке xk

долж-

ны удовлетворять условию б:

Sk (xk )= Sk +1 (xk ),

Sk′,x (xk )= Sk′+1,x (xk ),

Sk′′,xx (xk )= Sk′′+1,xx (xk ), k =

1,m −1.

Отсюда получается система линейных алгебраических уравнений (условия

непрерывности сплайна и его производных):

ak = ak+1 + bk+1 (xk − xk+1 )+ ck+1 (xk − xk+1 )2 2 + dk+1 (xk − xk+1 )3 6, k =

1, m −1,

bk = bk+1 + ck+1 (xk − xk+1 )+ dk+1 (xk − xk+1 )2 2, k =

1,m −1,

ck = ck +1 + dk+1 (xk − xk+1 ), k =

1,m −1

И наконец, условия в дают уравнения

Sk (xk ) = ak = fk ,

k =

1,m

Вводится обозначение: hk+1 = xk +1 − xk

– длины отрезков. Предыдущие вы-

ражения можно записать в виде общей системы линейных алгебраических

уравнений относительно искомых коэффициентов ak , bk , ck , dk ,

k =

1,m

= a

− b

+ c

2 − d

3 6, k =

(4.9)

k+1

1,m −1,

k+1

k+1 k +1

= b

− c

+ d

k =

(4.10)

1,m −1

k +1

k+1

k+1 k+1

101

Sxx′′ (a) = 0, Sxx′′ (b) = 0,


ck = ck+1 − dk+1hk+1, k =			1,m −1	,	(4.11)
ak = fk , k =		.			(4.12)
ak = fk , k =	1,m	.			(4.12)

Система (4.9)–(4.12) содержит 4m – 3 уравнения с 4m неизвестными. Кроме того, для точки x0 = a имеет место соотношение

S1 (x0 )= a1 + b1 (x0 − x1 )+ c1 (x0 − x1 )2 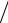2 + d1 (x0 − x1 )3 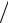6 = f0 .

Используя соотношения (4.12), в последнем выражении и уравнениях (4.9)

можно исключить неизвестные ak ,

k =

, а сами уравнения записать в форме

1,m

= f

− b

+ c

2 − d

6, k =

(4.13)

k+1

0,m −1

k+1

В результате получена система 3m – 2 уравнений (4.10), (4.11) и (4.13), со-

держащая 3m неизвестныхbk , ck , dk ,

k =

. Для «замыкания»

этой системы

1,m

уравнений следует принять

(4.14)

(4.15)

что соответствует «нулевым» кривизнам в начальной и конечной точках отрезка [a,b], то есть «свободным» концам сплайна. Возможны и иные условия для замыкания системы уравнений, например задание значения производной (наклона касательной) в конечной и/или начальной точках и некоторые другие. Условие (4.14) с помощью выражения (4.8) удобно представить в форме

S1′′,xx (x0 )= c1 − d1h1 = 0 ,

а формулу (4.15) – в виде

′′

(xm )= cm = 0 ,

Sm,xx

что позволяет переписать уравнения (4.11)

dk hk

= ck

− ck−1,

k =

c0 = 0,

cm = 0.

(4.16)

1,m

В итоге получена система 3m + 1 уравнений (4.10), (4.13), (4.16), содержа-

щих 3m + 1 неизвестную величину.

Рассматриваются два уравнения вида (4.13):

b h

= ( f

− f

k−1

)+ c

2 2 − d

h3 6,

k k

= ( f

− f

)+ c

− d

;

k+1

k+1 k+1

k+1

откуда следует

b = ( f

− f

k−1

) h

+ c

h 2 − d

2 6,

k k

( f

− f

)

+ c

− d

k+1

k+1 k+1

k+1

102

Полученные выражения для bk и bk+1 подставляются в уравнения (4.10):

−d

2 =

= ( f

)

k+1 k+1

k+1

− f

− ( f

− f

k−1

)

h + c

2 − d

6 − c h 2 + d

2 ,

k+1

k+1 k

k +1 k+1

k k

+ c h − 2d

3 − d

2 3 =

k+1 k

k k

+1 k+1

k k

= 2[( fk+1 − fk ) hk+1 − ( fk − fk−1 ) hk ], k =

1,m −1

Формулы (4.16) позволяют получить выражения

− c

−1

)h ,

= (c

k+1

− c

k k

k+1 k+1

k+1

благодаря чему предыдущее выражение преобразуется к виду

ck+1hk+1 + ck hk − 2(ck +1 − ck

)hk +1 3 − (ck − ck−1 )hk 3 =

= 2[( fk +1 − fk ) hk +1 − ( fk − fk −1 ) hk ], k =

1, m −1

Приведение подобных слагаемых и учет условий (4.14) и (4.15) приводит

к выражениям

−1hk +2ck (hk +hk+1 )+ck+1hk+1 = 6[( fk+1 − fk ) hk+1 −( fk − fk−1 ) hk ],

(4.17)

0, c

= 0, k =

1,m −1

В итоге получена система линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов. После решения системы уравнений (4.17)

и определения всех величин ck ,		k =		определяются искомые коэффициенты
и определения всех величин ck ,		k =	0,m	определяются искомые коэффициенты
сплайнов:
dk = (ck − ck−1 ) hk ,


ak = fk ,
	= c h 2 − d	h2	6 + ( f			− f		)	h , k =1,m.
b	= c h 2 − d	h2	6 + ( f		k	− f	k−1	)	h , k =1,m.
k	k k	k k			k		k−1		k

4.2.2. Сходимость процесса интерполяции кубическими сплайнами

Необходимо убедиться, что при увеличении числа m узлов на отрезке [a,b] последовательность сплайн-функций сходится к интерполируемой функции. Для упрощения рассматривается последовательность сеток с равномерным расположением узлов,

Ωm = {xk = a + hk, k = 0,m}, h = (b − a)m,

что приводит систему уравнений (4.17) к более простому виду:

−1

4ck

ck+1

6( fk−1

−

2 fk

fk+1 ) h

, k

1,m

−

= 0, c

= 0.

103

Предполагается, что аппроксимируемая функция f (x) непрерывна вместе со своими производными вплоть до четвертого порядка, то есть f C[4a,b], а также имеют место равенства

′′

fxx (a)

= 0, fxx (b) = 0.

Вводятся обозначения:

[a,b

]

= max

g(x)

– чебышёвская норма на отрезке [a,b],

x [a,b]

Ωm

= max

ϕ(xk )

– чебышевская норма на сеточной области Ωm ,

xk Ωm

h2 –

разностный аналог второй

производной

fk′′,xx = ( f (xk −1 ) − 2 f (xk ) + f (xk +1 ))

аппроксимируемой функции f

(x) в узле xk,

M 4 =

fxxxxiv

[a,b]

– оценка четвертойпроизводнойаппроксимируемой функции–

приводящие систему уравнений (4.17) к виду

′′

−1

4ck

ck+1

1,m

−

6 fk ,xx , k

(4.18)

= 0,

= 0.

Лемма 4.1. Для всех f (x) C[4a,b] справедлива оценка:

fxx′′ − Sxx′′ Ωm ≤ 3M 4h2 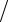4.

Доказательство. В силу определения введенной нормы на сеточной области необходимо проверить точки xk , для которых Sxx′′ (xk )= ck . Погрешность

аппроксимации определяется разностью

′′

= 0,m .

zk = ck − fxx (xk ), k

Для k = 0 и k = m, в частности, z0 = zm = 0 . Уравнения (4.18) в новых пере-

менных принимают вид

′′

−

′′

−1

4zk

zk+1

1,m

−

6 fk ,xx

[fxx (xk−1 )

4 fxx (xk )

fxx (xk+1 )], k

= 0,

= 0.

(4.19)

Вводится обозначение

′′

ψk = 6 fk ,xx

− [fxx (xk−1 )+ 4 fxx (xk ) + fxx (xk+1 )]=

′′

=6 [fk ,xx

− fxx (xk )]−

[fxx (xk−1 ) + 4 fxx (xk ) +

fxx

(xk +1 )]+ 6 fxx (xk )=

(4.20)

′′

−1 )

′′

= 6[fk,xx − fxx (xk )]−[fxx (xk

−2 fxx (xk )+ fxx (xk+1 )]=

′′

= 6[fk ,xx − fxx (xk )]

− ( fxx )k ,xx h

104

причем

′′

( fxx )k ,xx = [fxx (xk −1 )− 2 fxx (xk )+

fxx (xk+1 )]

– разностный аналог второй производной

′′

(xk ). Использование формулы

fxx

Тейлора для функции

f (x),

f (xk +1 )= f (xk )

′

(xk ) + h

′′

+ h

′′′

+ h

24 ,

+ hfx

fxx (xk )

fxxx (xk )

fxxxx (ξ)

f (xk−1 )= f (xk )

′

(xk ) + h

′′

− h

′′′

+ h

24,

− hfx

fxx (xk )

fxxx (xk )

fxxxx (ζ)

ξ (xk , xk +1 ), ζ (xk −1 , xk ),

и для ее второй производной		′′
и для ее второй производной		fxx (x),
′′	′′	′′′	2	iv
fxx (xk+1 )= fxx (xk )+ hfxxx (xk ) + h			2	iv
fxx (xk+1 )= fxx (xk )+ hfxxx (xk ) + h				fxxxx (η)
′′	′′	′′′	2	iv
fxx (xk−1 )= fxx (xk )− hfxxx (xk ) + h			2	iv
fxx (xk−1 )= fxx (xk )− hfxxx (xk ) + h				fxxxx (ϑ)

2, η (xk , xk+1 ), 2, ϑ (xk−1, xk ),

позволяет оценить погрешность разностных аппроксимаций производных:

fk′′,xx

( fxx′′ )k ,xx =

= [h

′′

24 + h

24] h

fxx (xk ) + h

fxxxx (ξ)

fxxxx (ζ)

′′

= fxx (xk )+ h

[fxxxx (ξ)+ fxxxx (ζ)] 24

[h2 fxxxxiv (η)

2 + h2 fxxxxiv (ϑ)

2] h2

= [fxxxxiv (η)+ fxxxxiv (ϑ)] 2 .

После подстановки полученных выражений в формулу (4.20)

′′

ψk

≤ 6

fk ,xx − fxx (xk )

( fxx )k ,xx h

≤

≤ h2

fxxxxiv

(ξ)

4 + h2

fxxxxiv (ζ)

4 + h2

fxxxxiv

(η)

2 + h2

fxxxxiv (ϑ)

– получается оценка

Ωm

= max

ψk

≤

≤ h2 max

xk Ωm

f iv

(ξ)

+ max

f iv

(ζ)

+ 2max

f iv

(η)

+ 2max

f iv

(ϑ)

ξ Ωm

xxxx

ζ Ωm

xxxx

η Ωm

xxxx

ϑ Ωm

xxxx

= 6h2

f iv

4 ≤ 3h2

f iv

[a,b]

2 = 3M

2 .

xxxx

Ωm

xxxx

Из формул (4.19) следует:

4zk = ψk − zk+1 − zk−1 ,

≤

ψk

zk−1

≤ max

ψk

+ max

zk+1

+ max

zk−1

+ 2

xk Ωm

Ωm

105

Поскольку эта оценка имеет место во всех точках сеточной области Ωm ,

она справедлива и в точке, где

достигает максимума, то есть

Следовательно,

≤

+ 2

≤

2 ≤ 3M

h2 4,

Ωm

откуда следует утверждение леммы 4.1.

Теорема 4.3. Для любой функции f C[4a,b] справедливы оценки:

f − S

[a,b]

≤ M 4 h4 ,

(4.21)

f ′− S′

[a,b] ≤ M 4 h3 ,

(4.22)

′′

fxx − Sxx

[a,b] ≤ M

(4.23)

Доказательство.

Рассматривается

произвольный отрезок [xk−1, xk ],

k =

. Определение сплайна (4.8), а также формулы (4.11) дают

1,m

Sk′′,xx (x) = ck + dk (x − xk )= ck + (ck − ck−1 )(x − xk ) h =

= ck (x − xk −1 ) h + ck −1 (xk − x) h,

или

Sk′′,xx (x) = αck + (1 − α)ck−1 ,

с использованием обозначений

α = (x − xk−1 ) h, 0 ≤ α ≤1.

Справедливо следующее тождество:

]}+

′′

fxx (x) − Sxx (x)={α[fxx

(xk ) − ck ]+ (1 − α)[fxx (xk−1 )− ck−1

′′

(xk

)]+

′′

(4.24)

+ {α[fxx (x)− fxx

(1 − α)[fxx (x)− fxx (xk−1 )]}.

Оценка первого слагаемого в правой части (4.24):

α[ fxx′′(xk ) −ck ]+ (1−α)[ fxx′′(xk−1) −ck−1 ] ≤ α fxx′′(xk ) − ck + (1−α) fxx′′(xk−1) − ck−1 ≤

≤ αmax

′′

+ (1 − α)max

′′

(x)− ck−1

fxx (xk )− ck

fxx

xk Ωm

′′

+ (1 − α)

′′

xk Ωm

′′

= α

fxx − Sk ,xx

fxx − Sk−1,xx

≤ 3M 4h

4 .

106

Для оценки второго слагаемого используется формула Тейлора

′′

′′′

fxx (xk )=

fxx (x)+ (xk

− x)fxxx (x)+ (xk

)

′′

− x)

fxxxx (ξk

′′

′′′

)

ξk ,ζk (xk−1, xk ).

fxx (xk−1 )= fxx (x)+ (xk−1 − x)fxxx (x)+ (xk−1 − x)

fxxxx (ζk

Отсюда получаются соотношения для разностей

′′

′′′

fxx (x)− fxx (xk )= (x − xk )fxxx (x)− (xk

(ξk

)

− x)

fxxxx

′′

′′′

fxx (x) − fxx (xk−1 )= (x − xk−1 )fxxx (x)− (xk−1 − x)

fxxxx (ζk )

Второе слагаемое в правой части формулы (4.24) преобразуется к виду

α[fxx

(x) − fxx (xk )]+

(1 − α)[fxx (x)− fxx (xk−1 )]=

= α (x − x

′′

(x)−(x − x) f

(ζ ) 2 =

′′′

(x)−(x − x) f

(ξ ) 2 +(1−α)(x − x

′′′

[

]

[

]

= f

xxx

xxxx k

k−1 xxx

k−1

) f

xxxx

(x)[α(x − x )+(1−α)(x − x )]− α(x − x

)

(ξ )+(1−α)(x − x

(ζ ) 2 =

′′′

k−1

[

k−1

]

xxx

xxxx

= f

′′′

(x)[(1 − α)αh − (1 − α)αh]− αh (1 − α) f

(ξ ) + (1 − α)α h f

(ζ ) 2 =

[

]

xxx

xxxx

= −αh2 (1 − α)[(1 − α)fxxxxiv (ξk ) + αfxxxxiv (ζk )]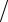2 .

Выполняется оценка

′′

≤

α[fxx (x)

− fxx (xk )]+(1−α)[fxx

(x)− fxx (xk−1 )]

≤ αh2 (1 − α) (1 − α)

fxxxxiv

(ξk )

+ α

fxxxxiv (ζk )

2 ≤

≤ M 4αh2 (1 − α) 2 ≤ M 4h2 8 .

При выводе последнего соотношения учтено, что

max

f iv

(x)

≤ max

f iv

(x)

= M

α(1 − α)≤1 4 .

x [xk −1 ,xk ]

xxxx

x [a,b]

xxxx

Оценивается левая часть тождества (4.24):

x [xk−1, xk ]. (4.25)

′′

fxx (x)− Sk (x)

≤ 3M

4 + M 4h

8 = 7M 4h

≤ M 4h

Поскольку выражение (4.25) справедливо для любого отрезка, его можно

использовать для оценки погрешности

′′

(x)

на всем рассматриваемом

fxx (x) − Sxx

отрезке [a,b]:

′′

(x)

≤ M 4h .

fxx (x)− Sxx

Отсюда получается

f ′′

− S′′

[a,b]

= max

f ′′

(x) − S′′

(x)

≤ M

x [a,b]

то есть утверждение (4.23) теоремы.

107

Для доказательства соотношения (4.22) на отрезке [xk−1, xk ]вводится вспомогательная функция r(x)= f (x)− Sk (x). Согласно определению сплайна, r(xk−1 )= r(xk )= 0 . Но тогда, в соответствии с теоремой Ролля1, существует хотя бы одна точка ξ [xk−1, xk ], rx′(ξ)= 0 . В этом случае, используя теорему Лагранжа, можно выполнить оценку

rx′(x) = rx′(x)− rx′(ξ) = rxx′′ (ζ)(x − ξ) ≤ rxx′′ (ζ)h ,

откуда с учетом соотношения (4.25) получается

′

≤

′′

h ≤ M 4h

(x) − Sk ,x (x)

fxx (ζ)− Sk ,xx (ζ)

Поскольку это

неравенство

справедливо на

любом отрезке [xk−1, xk ], с его

помощью можно получить утверждение (4.22)

теоремы:

′ − S′

[a,b]

= max

f ′(x) − S′

(x)

≤ M

h3 .

x [a,b]

Для получения последнего утверждения (4.21) на отрезке [xk−1, xk ] строится функция

g(t)= f (t) − Sk (t)− K(t − xk −1 )(t − xk ).

Из условия обращения этой функции в нуль в произвольно выбранной точ-

ке x [xk−1, xk ]

g(x) = f (x) − Sk (x) − K(x − xk−1 )(x − xk )= 0

определяется значение константы

K = [f (x) − Sk (x)]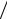(x − xk −1 )(x − xk ).

Очевидно, что теперь

g(x)= g(xk )= g(xk−1 )= 0 .

		′′
Это означает, что существует хотя бы одна точка ξ [xk−1, xk ], gxx (ξ) = 0.
Отсюда следует:
′′	′′	′′

gxx (ξ) = fxx (ξ) − Sk ,xx (ξ)− 2K = 0 ,

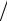fxx′′(ξ)− Sk′′,xx (ξ)= 2K = 2[f (x) − Sk (x)](x − xk−1 )(x − xk ), f (x) − Sk (x) = [fxx′′(ξ)− Sk′′,xx (ξ)](x − xk−1 )(x − xk )2 .

1 Ролль Мишель [21.4.1652 – 8.11.1719] – французский математик. С 1685 года является членом Парижской академии наук.

Теорема Ролля [2]: если функция f(x) непрерывна в замкнутом интервале [a,b], дифференцируема во всех его внутренних точках и имеет на концах интервала равные значения, то существует хотя бы одна точка ξ [a,b], f ′(ξ) = 0 .

108

Отсюда, с использованием неравенства (4.25), следует оценка отклонения значения сплайн-аппроксимации от значения функции для выбранной точки x [xk−1, xk ]:

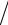f(x)− Sk (x) = fxx′′(ξ)− Sk′′,xx (ξ)(x − xk−1 )(x − xk )2 ≤

≤M 4h2 (x − xk−1 )(x − xk )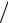2 ≤ M 4h4 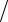8.

Здесь учтено, что

max

(x − xk−1 )(x − xk )

= h2

4 .

x [xk −1 ,xk ]

Поскольку последнее неравенство справедливо для любого x [xk−1, xk ],

отсюда следует выражение (4.21) теоремы:

f − S

[a,b]

= max

f (x)− Sk (x)

≤ M 4h4

8 ≤ M 4h4 ,

x [a,b]

что и требовалось доказать.

4.3. Наилучшее приближение в гильбертовом1 пространстве

Рассматривается линейное нормированное пространство H, в котором задана конечная система линейно-независимых элементов ϕk H , k = 0,m. Требуется заменить элемент f H линейной комбинацией

m
ϕ = c0ϕ0 + c1ϕ1 +…+ cmϕm = ∑ck ϕk ,	(4.26)

k=0

где ϕ – обобщенный полином. Задача о наилучшем приближении заключается в поиске среди множества линейных комбинаций вида (4.26) такой, для кото-

		m
рой отклонение	f	− ∑ck ϕk		было бы наименьшим. Такой элемент (обобщен-
		k=0
~		m ~	является элементом наилучшего приближения. Для
ный полином) ϕ =		∑ck ϕk	является элементом наилучшего приближения. Для

k=0

построения элемента наилучшего приближения в гильбертовом пространстве H определяется норма,

1 Гильберт Давид [23.1.1862 – 14.2.1943] – немецкий математик, иностранный членкорреспондент (1922) и иностранный почетный член (1934) АН СССР. Окончил Кенигсбергский университет. В 1893–95 годах – профессор этого же университета. С 1895 по 1930 год – профессор Геттингенского университета. Исследования Гильберта оказали большое влияние на развитие многих разделов математики: теорию инвариантов, теорию алгебраических чисел, основания геометрии, вариационное и дифференциальное исчисление, интегральные уравнения, основы математической физики, логические основы математики. В 1904 году Гильберту присуждена международная премия имени Н.И. Лобачевского.

109

		= ( f , f )1H2	b	1 2
f	H	= ( f , f )1H2	= ∫ f 2	(x)dx	,
			a

порожденная скалярным произведением

( f , g)H = ∫b f (x)g(x)dx .

Рассматривается отклонение приближения (4.26) от элемента f:

	2		m	m
	2
						=
f − ϕ	H	=	f − ∑ck ϕk , f − ∑c j ϕj			=
f − ϕ	H	=	f − ∑ck ϕk , f − ∑c j ϕj
			k=0	j=0	H

−

∑ck ϕk ,

(4.27)

= ( f , f )H −

f , ∑c j ϕj

∑c j ϕj

j=0

k=0

j=0

2H − 2∑ck ( f , ϕk )H +

∑ck c j (ϕk , ϕj )H .

k=0

k , j=0

Вводятся обозначения:

A – матрица с компонентами akj = (ϕk , ϕj )H ,

k, j =

0,m

c – вектор коэффициентов {c0 , c1,…, cm }T ,

fˆ – вектор {f0 ,

f1,…,

fm }T , fk = ( f , ϕk )H , k =

0,m

Скалярное произведение векторов определяется обычным образом:

(u,v)= ∑uk vk , u,v Rm+1 .

k=0

Теперь выражение (4.27) можно представить следующим образом:

− ϕ

2H = (Ac,c)− 2( fˆ,c)+

2H .

(4.28)

Очевидно,

что поиск элемента ϕ H наилучшего приближения сводится

теперь к поиску минимума функционала

F(c) = (Ac,c) − 2( fˆ,c),

(4.29)

поскольку слагаемое

2H в выражении (4.28) от параметров ck , k =

не за-

0,m

висит. Матрица A симметрична, поскольку akj

= (ϕk ,ϕj )H = (ϕj ,ϕk )H

= a jk . Если

положить f = 0, то из соотношения (4.28) следует:

(Ac,c)=

2 ≥ 0 c Rm+1 .

Если для

какого-либо

элемента c′ Rm+1

имеет

место

равенство

′ ′

) = 0 ,

то

из

равенства

следует,

что

(Ac ,c

H = 0

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 4311 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.2022336.71 Кб11Методические указания по выполнению лабораторных работ по дисциплине..pdf
#
15.11.2022828.38 Кб7МЕТОДИЧЕСКОЕ РУКОВОДСТВО К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ ПО ДИСЦИПЛИНЕ «ЭЛЕКТРОПРИВОД».pdf
#
15.11.2022828.38 Кб2Методическое руководство к выполнению курсовой работы по дисциплине..pdf
#
15.11.202211.77 Mб22Методология научных исследований в сварке..pdf
#
15.11.20224.74 Mб29Методы выделения очистки и идентификации органических веществ..pdf
#
15.11.20223.42 Mб17Методы вычислительной математики..pdf
#
15.11.20225.46 Mб39Методы и инструменты поиска инновационных решений..pdf
#
15.11.20221.38 Mб7Методы и механизмы инноваций и предпринимательства..pdf
#
15.11.20222.42 Mб1Методы и модели в экономике Часть 1..pdf
#
15.11.202214.5 Mб7Методы и средства диагностики несущей способности изделий из компози..pdf
#
15.11.202211.79 Mб23Методы и средства защиты человека от опасных и вредных производственн..pdf