Методы вычислительной математики

9.4. Метод Галеркина1

Метод Галеркина отличается от метода моментов тем, что в качестве взвешивающих функций используются те же самые пробные функции, то есть

Использование метода Галеркина рассматривается применительно к частному случаю линейного дифференциального уравнения второго порядка

Первое слагаемое этого выражения преобразуется следующим образом:

Учитывая, что граничные условия заданы в виде (9.17), пробные функции выбираются из условия

ϕj (a) = ϕj (b)= 0, j =1,m,

в 1899 году. Работал на Харьковском паровозостроительном заводе. Начал свою плодотворную научную деятельность в тюрьме, куда попал за свои антимонархические убеждения. Первое назначение на педагогическую деятельность получил в 1909 году в СанктПетербургском политехническом институте; в 1920 году стал деканом факультета прикладной механики. Был избран членом-корреспондентом АН СССР с 1928 года, действительным членом Академии наук СССР – с 1935 года. В 1942 году получил Государственную премию

СССР. В 1941 и 1945 годах был удостоен орденов Ленина.

201

что приводит к упрощению выражения (9.18):

В последнее соотношение подставляется представление (9.14) искомой функции в виде ряда и выполняются преобразования:

последнее выражение можно представить в виде системы линейных алгебраических уравнений

k=1

относительно коэффициентов ak , k =1,m , разложения (9.14) решения в ряд по пробным функциям. Эта система имеет симметричную матрицу коэффициентов, поскольку очевидно, что Ckj = C jk . Необходимо отметить, что в случае за-

дания граничных условий в форме (9.13) разрешающие соотношения (9.18) приводятся к виду (9.19) с иными значениями коэффициентов,

Пример 9.3. Решить уравнение стационарной теплопроводности

(λθ′x (x))′x + J (x)= 0

202

для стержня единичной длины, теплоизолированного с боковой поверхности; полагается, что на левом и правом торцах поддерживается заданная температу-

ра θ(0) = θ0 , θ(1)= θ1 ; λ = const, J = const.

Система пробных функций строится на основе системы полиномов. В качестве «нулевой» выбирается линейная функция ϕ0 (x)= θ0 + (θ1 − θ0 )x . Осталь-

Для рассматриваемого уравнения, в отличие от выражения (9.16), функция q(x) = 0. Рассчитываются коэффициенты системы уравнений (9.19):

C11 = −∫1 (pϕ1′,xϕ1′,x + qϕ1ϕ1 )dx = −λ∫1 (ϕ1′,x )2 dx = −λ∫1 (2x −1)2 dx = −λ3 ,

0 0 0

C12 = C21 = −λ∫1 ϕ1′,xϕ′2,x dx = −λ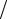6 ,

0

C13 = C31 = −λ∫1 ϕ1′,xϕ′3,x dx = −λ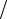10,

0

C22 = −λ∫1 (ϕ′2,x )2 dx = −2λ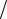15 ,

0

Система линейных алгебраических уравнений (9.19) принимает вид

203

Решение этой системы дает коэффициенты разложения a1 = −J2λ, a2 = 0, a3 = 0,

позволяющие записать решение в виде

y3 (x) = θ0 + (θ1 − θ0 )x − J (x −1)x 2λ = θ0 + (θ1 − θ0 + J 2λ)x − Jx2 2λ.

Полученное решение является точным для поставленной задачи. Пример 9.4. Решить уравнение стационарной теплопроводности

(λθ′x )′x + J (x)= 0

для стержня единичной длины, теплоизолированного с боковой поверхности.

где α – коэффициент теплоотдачи в окружающую среду с температурой θcp ;

λ = const, J = const.

Как и в предыдущем примере, ϕ0 (x) = G + Hx. Коэффициенты G и H подбираются из условия удовлетворения заданным граничным условиям ϕ0 (0)= θ0

Отсюда следует, что

H = α(θср − θ0 )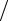(α + λ).

Таким образом, «нулевая» пробная функция представляется в виде

ϕ0 (x) = θ0 + α(θcp − θ0 ) x / (α + λ).

Остальные пробные функции представляются в форме, удовлетворяющей однородным условиям задачи,

ϕ1 (x) = [x − (α + 2λ)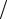(α + λ)] x , ϕ2 (x)= [x2 − (α + 2λ)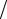(α + λ)] x ,…,

ϕk (x) = {xk − [α + (1 + k )λ]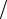(α + λ)} x.

204

Подсчитываются коэффициенты системы уравнений (9.19) в соответствии с формулами (9.20):

−λ{(k +1)( j +1)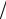(k + j +1)−[2α+(k + j +2)λ]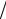(α+λ)+[α+(k +1)λ][α+( j +1)λ]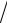(α+λ)2 },

1 1

f j = −J ∫ϕj dx + λ∫ϕ′0,xϕ′j,x dx − λ[ϕ′0,xϕj ]10=

00

=−J{2(α + λ)−[α + ( j +1)λ]( j + 2)}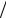2(α + λ)( j + 2).

Для упрощения принимается m = 3. Система уравнений (9.19) имеет вид

Решением этой системы являются коэффициенты a1 = −J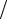2λ, a2 = 0, a3 = 0

разложения решения в ряд по пробным функциям:

y3 (x) = θ0 + α(θ1 −θ0 )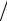(α + λ)x − J[x −(α + 2λ)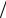(α + λ)]x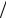2λ =

= θ0 + [α(θ1 − θ0 )+ (α + 2λ)J 2λ]x (α + λ) − Jx2 2λ.

Полученное решение является точным для поставленной задачи.

9.4.1. Разрешимость системы алгебраических уравнений метода Галеркина

Рассматриваются условия существования и единственности решения системы алгебраических уравнений (9.19), полученных в результате применения метода Галеркина к задаче (9.16)–(9.17).

Теорема 9.1. Пусть коэффициенты дифференциального уравнения (9.16) удовлетворяют условиям

205

Тогда система алгебраических уравнений метода Галеркина (9.19) имеет единственное решение.

Доказательство. В однородную систему уравнений, соответствующую системе (9.19),

k=1

подставляются значения коэффициентов

Cjk =−∫b (pϕ′k,xϕ′j,x +qϕk ϕj )dx,

a

определенные ранее:

m

zm = ∑bk ϕk , k=1

полученное выражение можно записать в виде

∫b (pϕ′j,x z′m,x + qϕj zm )dx = 0, j =1,m .

a

Каждое из этих выражений умножается на bj , и все полученные соотношения суммируются:

= ∫b [p(z′m,x )2 + q(zm )2 ]dx = 0.

a

При выполнении условий (9.21) приведенное выражение справедливо лишь в том случае, когда z′m,x (x) = 0. Это означает, что функция

m

zm (x) = ∑bk ϕk (x) = const.

k =1

206

Из условия, что на концах отрезка [a, b] по построению все функции ϕk обращаются в нуль,

ϕk (a)= ϕk (b) = 0, k =1,m ,

получается:

n

zn (x) = ∑bk ϕk (x)= 0,

k=1

откуда в силу линейной независимости ϕk следует: bk = 0, k =1,m . Но это означает, что однородная система алгебраических уравнений (9.22) имеет только тривиальное решение, то есть ее определитель отличен от нуля, что и говорит о существовании единственного решения исходной системы уравнений (9.19). Что и требовалось доказать.

9.5. Метод наименьших квадратов

Для решения линейного дифференциального уравнения второго порядка

условиям, перечисленным в разделе, посвященном методу моментов. Это позволяет представить решение задачи (9.23), (9.24) в виде разложения (9.14) в ряд по этим функциям. Подстановка (9.14) в уравнение (9.23) дает невязку

207

данному уравнению (9.23). Функционал Φ(ym ) можно рассматривать как функ-

цию m переменных ak , k =1,m , и записать необходимые условия экстремума

a

соотношения (9.25) можно представить в виде системы линейных алгебраиче-

Из построения видно, что эта система уравнений имеет симметричную матрицу коэффициентов, C jk = Ckj .

Пример 9.5. Решить уравнение стационарной теплопроводности

(λθ′x (x))′x + J (x) = 0

208

для стержня единичной длины, теплоизолированного с боковой поверхности, сграничнымиусловиями θ(0) = θ0 , θ(1)= θ1 . Полагается, что λ = const, J = const.

Для решения поставленной задачи используется система пробных функций, аналогичная рассмотренной в примере 9.3:

Число слагаемых в разложении (9.14) ограничивается m = 3. В этом случае коэффициенты системы уравнений (9.26) принимают значения:

имеет решение –

a1 = −2J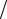λ, a2 = 0, a3 = 0,

позволяющее построить точное решения исходной задачи: y3 (x) = θ0 + (θ1 − θ0 + J2λ)x − Jx2 2λ .

9.5.1. Разрешимость системы уравнений метода наименьших квадратов

Рассматривается однородная система линейных алгебраических уравнений, построенная на основе системы (9.26),

m

∑C jk bk = 0, j =1,m.

k=1

209

В это выражение подставляются значения коэффициентов C jk , и выполняются преобразования:

a

m

Здесь использовано обозначение: zm = ∑bk ϕk. Каждая из предыдущих

k=1

формул умножается на bj , и все полученные выражения суммируются:

m

тривиальное решение zm = ∑bk ϕk = 0. В силу линейной независимости проб-

k=1

ных функций ϕk это возможно лишь при условии bk = 0, k =1,m , то есть однородная система алгебраических уравнений имеет только тривиальное решение. Отсюда следует, что определитель этой системы уравнений отличен от нуля, а это является необходимым и достаточным условием ее разрешимости. Прове-

210