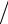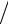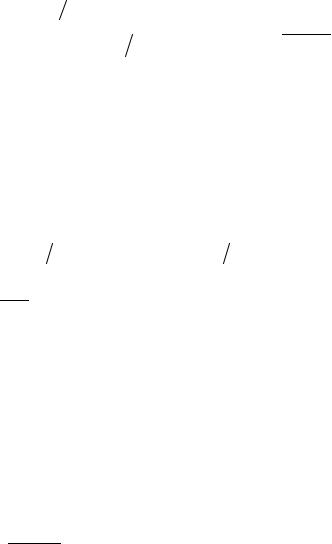
= y |
|
[A +2B u |
|
+C |
u |
u |
|
|
|
]+[2B v |
|
|
|
+C |
|
u |
v |
|
+C |
v |
|
]= f |
|
h2 , k = |
|
|
k+1 |
k+1 |
k+1 |
k+1 |
|
k+1 |
k |
k |
1,m −1, |
|
k |
k |
|
|
|
|
k |
k |
|
|
|
|
k |
|
|
k |
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
которое выполняется при любом наборе значений |
yk , k = |
|
|
, |
если имеют |
1,m −1 |
место равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ak + 2Bk uk+1 + Ck uk uk+1 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2B v |
k +1 |
+ C |
|
u |
v |
k +1 |
+ C |
|
v |
k |
− f |
k |
= 0, k =1,m −1. |
|
|
|
|
|
|
|
k |
|
|
k |
|
k |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это |
позволяет |
получить |
|
рекуррентные |
|
соотношения для |
вычисления |
uk и vk : |
uk+1 = − Ak (2Bk + Ck uk ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(9.44) |
|
|
|
|
= (f |
|
h2 |
− C |
v |
|
) (2B |
|
+ C |
u |
|
|
), k = |
1,m −1. |
|
|
|
|
|
|
v |
k+1 |
k |
k |
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Прямой ход метода прогонки выполняется в следующей последовательности. Записывается выражение (9.43) для k = 0,
y0 = u1 y1 + v1 ,
и сравнивается с разностным аналогом граничного условия
y0 = α1 y1 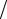 (α1 − α0h) − Ah
(α1 − α0h) − Ah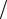 (α1 − α0h)
(α1 − α0h)
сеточной задачи (9.42). Отсюда можно вычислить начальные значения
u1 = α1 (α1 − α0h), v1 = − Ah (α1 − α0h). |
(9.45) |
Далее используются формулы (9.44) для определения всех остальных величин uk , vk , k = 2,m . Для выполнения обратного хода метода прогонки формула (9.43) при k = m – 1, то есть
ym−1 = um ym + vm ,
подставляется в разностный аналог второго граничного условия системы (9.42), ym =β1 (um ym + vm )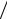 (β1 + β0h)+ Bh
(β1 + β0h)+ Bh (β1 + β0h),
(β1 + β0h),
ym [1 −β1um  (β1 + β0h)]= (β1vm + Bh)
(β1 + β0h)]= (β1vm + Bh)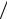 (β1 + β0h),
(β1 + β0h),
ym = (β1vm + Bh) (β1 + β0h −β1um ).
(β1 + β0h −β1um ).
Далее, с использованием соотношения (9.43), определяются все искомые величины yk , k = 0,m −1.
Метод прогонки можно использовать в тех случаях, когда в приведенных формулах знаменатели дробей не обращаются в нули. В частности, можно избежать равенства нулю выражения α1 − α0h в формулах (9.45) подбором соответствующего значения шага интегрирования h. При выполнении условий

A |
|
≠ 0, |
C |
|
|
≠ 0, |
|
2B |
|
≥ |
|
A |
|
+ |
|
C |
|
|
, k = |
|
|
|
k |
k |
1,m −1, |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
α |
|
(α |
|
− α |
|
h) ≤1, β |
(β + β |
h) |
|
(9.46) |
|
1 |
1 |
0 |
<1 |
|
|
|
|
|
|
|
1 |
|
1 |
0 |
|
|
|
|
|
|
знаменатели дробей |
2Bk + Ck uk и |
β1 |
+ β0h −β1un отличны от нуля. Для дока- |
зательства этого утверждения оцениваются значения переменных uk , k =1,m . Согласно условиям (9.46)
u1 = α1 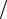 (α1 − α0h) ≤1.
(α1 − α0h) ≤1.
Предполагается, что uk ≤1 для произвольного значения k. Тогда, с учетом соотношений (9.46), получается неравенство
2Bk + Ck uk ≥ 2Bk − Ck uk = 2Bk − Ck 
 uk ≥ 2Bk − Ck ≥ Ak > 0 ,
uk ≥ 2Bk − Ck ≥ Ak > 0 ,
показывающее, |
|
что знаменатель 2Bk + Ck uk ≠ 0. Более того, из неравенства |
|
2Bk + Ck uk |
|
≥ |
|
Ak |
|
следует: |
|
|
|
|
uk+1 = Ak 
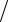
 2Bk + Ck uk ≤1.
2Bk + Ck uk ≤1.
Тем самым по индукции показано, что все uk ≤1, k =1,m . Согласно условиям (9.46) β1 < β1 + β0h . Тогда и знаменатель
β1 + β0h −β1un ≥ β1 + β0h − β1un = β1 + β0h − β1 
 un ≥ β1 + β0h − β1 > 0
un ≥ β1 + β0h − β1 > 0
отличен от нуля.
Контрольные вопросы и задания
9.1. Поясните необходимость каждого из требований, предъявляемых к системам функций ψk и ϕk в методах моментов, Галеркина, Ритца и наи-
меньших квадратов.
9.2.При каких условиях полная система функций будет одновременно замкнутой?
9.3.Решите задачу из примера 9.4 с помощью системы пробных функций
ϕ1 (x) = (x −1)x, ϕ2 (x)= (x −1)2 x, …, ϕk (x)= (x −1)k x.
9.4. Выражение (9.33) в методе Ритца определяет лишь условие стационарности функционала. При каких условиях функционал Φ(yn ) будет иметь
единственный минимум?
9.5. В методе Ритца приближенное решение строится на основе функций из класса C[1a,b], которые в общем случае не являются дважды дифференцируе-
мыми, что требуется для удовлетворения дифференциального уравнения (9.16). Поясните, в каком смысле в этом методе понимается сходимость приближенного решения к точному.
9.6. Решите задачу из примера 9.4, используя систему пробных функций
ϕ1 |
|
α+2λ |
|
α+3λ |
2 |
|
α+(k +1)λ |
k |
. |
(x) = x − |
x, ϕ2 |
(x) = x − |
x |
,…, ϕk (x) = x − |
α+kλ |
x |
|
|
α+λ |
|
α+2λ |
|
|
|
|
|
9.7. Погрешность аппроксимации (9.41) определяется не только степенью шага интегрирования h, но и ограниченностью значений производ-
ных |
′′′ |
iv |
yxxx (xk ), yxxxx (xk ). Установите, при каких условиях решение уравнения |
(9.23) будет иметь на отрезке [a, b] ограниченные значения производных до четвертого порядка включительно.
9.8.Предложите свою разностную схему аппроксимации уравнения (9.23)
иоцените ее погрешность.
9.9.Оцените порядок аппроксимации граничных условий (9.24) разностным аналогом (9.37). Предложите способ повышения порядка аппроксимации граничных условий.
9.10.Сопоставьте по эффективности метод Гаусса и метод прогонки для решения системы линейных алгебраических уравнений сеточной задачи.
9.11.Теорема 9.2 доказана для задачи (9.16) с граничными условиями (9.17). Установите условия разрешимости системы алгебраических уравнений (9.19) для задачи (9.16) с граничными условиями более общего вида (9.13).
10.ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
Вобщем случае дифференциальное уравнение второго порядка в частных производных представляется в виде1
Φ(x1 |
,…, xn , y, y′x ,…, y′x |
, y′x′x |
,…, y′x′x |
,…, y′x′ x |
)= 0. |
|
1 |
n |
1 1 |
i j |
n |
n |
Если уравнение представимо в виде |
|
|
|
n |
|
+ F(x1,…, xn , y, y′x1 ,…, y′xn )= 0, |
∑aij (x1,…, xn )y′x′i xj |
i, j=1 |
|
|
|
|
|
|
оно называется квазилинейным относительно старших производных. В случае,
когда F(x1,…, xn , y, y′x ,…, y′x |
) – функция, линейная относительно каждого из |
|
1 |
|
n |
аргументов y, y′x |
,…, y′x , |
последнее выражение представляется в форме линей- |
1 |
n |
|
|
ного дифференциального уравнения |
n |
|
n |
∑aij (x1,…, xn )y′x′i x j |
+ ∑bi (x1,…, xn )y′xi + c(x1,…, xn )y = f (x1,…, xn ). |
i, j=1 |
|
i=1 |
При f (x1,…, xn )= 0 |
уравнение становится однородным. Если aij , bi , c не |
зависят от аргументов x1,…, xn , получается линейное однородное дифференци-
альное уравнение в частных производных с постоянными коэффициентами. Наиболее хорошо изучены линейные дифференциальные уравнения второго порядка относительно функций двух аргументов
′′ |
′′ |
|
′′ |
′ |
|
′ |
(10.1) |
a11(t,x)ytt |
+2a12 (t,x)ytx +a22 |
(t,x)yxx +b1(t,x)yt +b2 |
(t,x)yx +c(t,x)y = f (t,x). |
Если в некоторой области G дискриминант уравнения [1] |
|
|
|
= a2 |
(t,x)− a |
(t,x)a |
22 |
(t,x) > 0, |
|
|
|
12 |
11 |
|
|
|
выражение (10.1) является дифференциальным уравнением гиперболического типа. Если дискриминант < 0, то уравнение (10.1) является эллиптическим. В случае = 0 уравнение относится к параболическому типу.
10.1. Некоторые дифференциальные уравнения второго порядка
Постановки задач математической физики рассматриваются на примере простейших дифференциальных уравнений второго порядка в частных производных [1].
1 Для функции y(t, x) двух переменных t и x дифференциальное уравнение принимает вид Φ(t, x,y,yt′,y′x ,ytt′′,ytx′′,y′xx′ ) = 0.
224

10.1.1. Уравнение теплопроводности |
|
Теплопередача в тонком |
прямолинейном однородном |
изолированном |
с боковой поверхности стержне описывается уравнением |
|
′ |
′′ |
(10.2) |
θt |
− ηθxx = 0. |
Здесь и далее обозначено: θ = θ(t, x) – температурное поле, t – время, t [0, ∞) ,
λ, c, ρ – коэффициенты теплопроводности, теплоемкости и плотности материала стержня, η = λ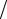 cρ – коэффициент температуропроводности, x – продольная
cρ – коэффициент температуропроводности, x – продольная
координата, x [0, L]. Для уравнения (10.2), записанного в виде
0 θ′tt′ + 2 0 θ′tx′ − ηθ′xx′ + θ′t = 0,
дискриминант
= a122 (t,x)− a11(t,x)a22 (t,x) = 0 − 0 (− η) = 0,
то есть уравнение относится к параболическому типу. Единственность решения уравнения (10.2) обеспечивается начальными
θ(0, x)= Θ(x) |
(10.3) |
и граничными условиями1 |
|
θ(t,0) = θ0 (t), θ(t, L) = θL (t). |
(10.4) |
Для получения непрерывного решения задачи (10.2)–(10.4) необходима согласованность краевых условий,
Θ(0) = θ(0,0) = θ0 (0), Θ(L) = θ(0, L) = θL (0).
Ограничения (10.4) на решение задачи (10.2) относятся к граничным условиям первого рода. Для задачи теплопроводности может быть записано граничное условие (например, на правом конце стержня) второго рода
λθ′x (t, L) = −q(t), |
(10.5) |
где q(t) – тепловой поток2 через торцевую поверхность. При теплообмене между торцевой поверхностью стержня и внешней средой, имеющей температуру θср, тепловой поток определяется выражением
q(t ) = α θ(t, L) −θcp (t ) , |
|
|
что приводит к граничному условию третьего рода
1В дальнейшем совокупность начальных и граничных условий называется краевыми условиями.
2Поток считается положительным, если он направлен внутрь тела.
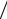
|
x ( ) |
( |
) |
|
( ) |
′ |
t, L |
= −α θ |
t, L −θ |
cp |
t , |
λθ |
|
|
которое можно записать как смешанное граничное условие |
αθ(t, L) + λθ′x (x, L)= αθср(t). |
(10.6) |
Очевидно, что граничные условия (10.4) и (10.5) можно рассматривать как частные случаи условия (10.6).
10.1.2. Уравнение свободных поперечных колебаний струны
В предположении о малости колебаний поведение нерастяжимой струны, находящейся под действием растягивающей силы F, описывается дифференциальным уравнением
′′ |
′′ |
ρ = 0, |
(10.7) |
utt |
− Fuxx |
где u(t, x) – вертикальное перемещение точек струны. Дискриминант
= a122 (t,x)− a11(t,x)a22 (t,x)= 0 −1 (− F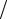 ρ)= F
ρ)= F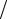 ρ > 0,
ρ > 0,
то есть уравнение относится к гиперболическому типу. Единственность решения уравнения (10.7) обеспечивается начальными
u(0, x) = U (x), |
ut′(0, x) =V (x) |
(10.8) |
и граничными условиями |
|
|
|
u(t,0) =U 0 (t), |
u(t, L)=U L (t). |
(10.9) |
Для получения непрерывного решения задачи (10.7)–(10.9) также необхо- |
дима согласованность краевых условий: |
|
|
U (0)=U 0 (0), |
U ′0 |
(0)=V (0), |
|
|
t |
|
(10.10) |
|
U ′L |
(0) =V (L). |
U (L) =U L (0), |
|
|
t |
|
|
10.1.3. Уравнение стационарной диффузии
Перенос и рассеяние примеси движущимся потоком (жидкости или газа) в плоской (двумерной) области G (вертикальной или горизонтальной) с границей ∂G моделируются уравнением диффузии
′ |
′ |
′′ ′′ |
(10.11) |
vxCx + vyCy − μ(Cxx + Cyy )= 0, |
где C = C(x, y) – концентрация примеси, vx, vy – компоненты вектора скорости потока, μ – коэффициент диффузии. Дискриминант уравнения
= a122 (x,y)− a11 (x,y)a22 (x,y) = 0 − μ μ = −μ2 < 0
позволяет отнести соотношение (4.11) к эллиптическому типу. Граничные условия для уравнения (10.11) могут записываться в форме условий:
– первого рода C(x,y)= C∂G (x,y), x,y ∂G1 ; |
|
– второго рода μCn′(x,y)= −q(x,y), x,y ∂G2 ; |
(10.12) |
– третьего рода μCn′(x,y) = −β[C(x,y)− Cср(x,y)], |
x,y ∂G3, |
где n – вектор внешней нормали к границе ∂G . |
|
10.2. Дифференциальные уравнения для функций нескольких переменных
При классификации дифференциальных уравнений второго порядка, записанных в канонической форме для функций n переменных, используется следующее правило. Дифференциальное уравнение в частных производных
n |
n |
+ c(x1,…,xn )y = f (x1,…,xn ) |
∑aii (x1,…,xn )y′x′i xi + ∑bi (x1,…,xn )y′xi |
i=1 |
i=1 |
|
|
|
|
|
|
|
|
является: |
|
|
|
|
|
|
|
|
|
– эллиптическим, если все aii (x1,…, xn ), |
i = |
|
|
|
имеют один и тот же знак |
1, n |
и все отличны от нуля; |
если все aii (x1,…, xn ), |
|
|
|
|
|
|
|
– гиперболическим, |
|
i = |
|
|
, кроме одного, имеют |
|
1, n |
один и тот же знак и все отличны от нуля; |
|
|
|
|
|
|
|
|
– параболическим, если все aii (x1,…, xn ), |
i = |
|
, кроме одного, отличны |
1, n |
от нуля и имеют один и тот же знак.
Уравнение стационарной диффузии (при отсутствии движения среды)
Cxx′′ + C′yy′ + Czz′′ = 0
является эллиптическим. Уравнение нестационарной теплопроводности
θ′t − η[θ′xx′ + θ′yy′ + θ′zz′ ]= 0
является параболическим. Уравнение малых поперечных колебаний мембраны utt′′ − F(u′xx′ + u′yy′ )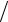 ρ = 0
ρ = 0
всюду гиперболично.
10.3. Метод Фурье разделения переменных
Метод разделения переменных рассматривается на примере решения задачи теплопроводности (10.2)–(10.4) с однородными граничными условиями при дополнительном предположении, что η = λ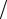 cρ =1,
cρ =1,
θ′t − θ′′xx = 0; |
|
|
|
|
|
|
θ(t,0) = 0, |
θ(t, L) = 0. |
θ(0, x) = Θ(x); |
|
|
|
Решение этой задачи разыскивается в форме
θ(t, x)=T (t)X (x).
T(t) – функция только времени t, а X(x) – функция только координаты x. Решение (10.14) подставляется в дифференциальное уравнение (10.13),
X (x)Tt′(t) −T (t)X xx′′ (x) = 0, Tt′(t) T (t) = X xx′′ (x)
T (t) = X xx′′ (x)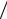 X (x).
X (x).
Поскольку левая часть последнего выражения зависит только от t, а правая – только от x, равенство возможно лишь в случае
Tt′(t)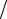 T (t)= X xx′′ (x)
T (t)= X xx′′ (x)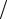 X (x)= −κ2 = const .
X (x)= −κ2 = const .
В результате получено два обыкновенных дифференциальных уравнения:
Tt′(t) + κ2T(t)= 0, X xx′′ (x) + κ2 X (x)= 0,
решения которых известны:
T (t) = C1e−κ2t ,
X (x)= C2 sin(κx)+ C3 cos(κx).
Здесь C1, C2, C3 – постоянные интегрирования. С использованием обозначений A = C1C2 , B = C1C3 решение (10.14) представляется в виде
θ(t, x)= e−κ2t [Asin(κx)+ Bcos(κx)].
ДляопределенияпостоянныхA иB используютсяграничныеусловия(10.13):
θ(t,0) = e−κ2t [A 0 + B 1]= 0, B = 0 ;
θ(t, L)= e−κ2t [Asin(κL)+ Bcos(κL)]= 0, |
Asin(κL) = 0 . |
Очевидно, что значение A = 0 приводит |
к тривиальному решению |
θ(t, x)≡ 0 , что противоречит начальному условию задачи (10.13). Выполнение равенства
sin(κL) = 0
возможно в случае κL = πp, откуда получается κp = πp L, p =1,2,…. Таким образом, получено множество решений вида (10.14):
L, p =1,2,…. Таким образом, получено множество решений вида (10.14):
θp (t, x) = Ape−π2 p2t L2 sin(πpx
L2 sin(πpx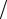 L), p =1,2,….
L), p =1,2,….

В силу линейности дифференциального уравнения (10.13) выражение
∞
∑ Ape−π2 p2t L2 sin(πpx L)
L)
p=1
также является решением задачи. При t = 0 этот ряд должен удовлетворять начальному условию (10.13). Иными словами, следует так подобрать коэффициенты Ap, чтобы
∞
∑ Ap sin(πpx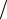 L)= Θ(x).
L)= Θ(x).
p=1
Функция Θ(x) может быть представлена разложением в ряд Фурье:
∞
Θ(x)= ∑Φp sin(πpx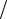 L),
L),
p=1
где Φp = 2∫L Θ(x)sin(πpx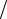 L)dx
L)dx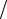 L . Сравнение двух последних выражений позво-
L . Сравнение двух последних выражений позво-
0
ляет получить решение задачи (10.13) в окончательном виде:
∞ |
L |
θ(t, x) = ∑ Ape−π2 p2t L2 sin(πpx L), |
Ap = 2∫Θ(x)sin(πpx L)dx L. |
p=1 |
0 |
С помощью полученного выражения может быть записано приближенное решение этой задачи:
m |
|
θm (t, x)= ∑ Ape−π2 p2t L2 sin(πpx L). |
(10.15) |
p=1
Вчастном случае при Θ(x)= Θ0 = const
Ap = 2Θ0 ∫L sin(πpx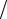 L)dx L = 4Θ0 πp, p =1,3,5,…
L)dx L = 4Θ0 πp, p =1,3,5,…
0
и формула (10.15) принимает более простой вид:
m
∑e−π2 p2t L2 sin πpx L p .
πp=1,3,5,…
10.4.Основные понятия и определения теории разностных схем) ( )( ][4Θ
Решение одномерной задачи (10.2)–(10.4) разыскивается в области
G ={(t, x) t [0,T ], x [0, L]}.
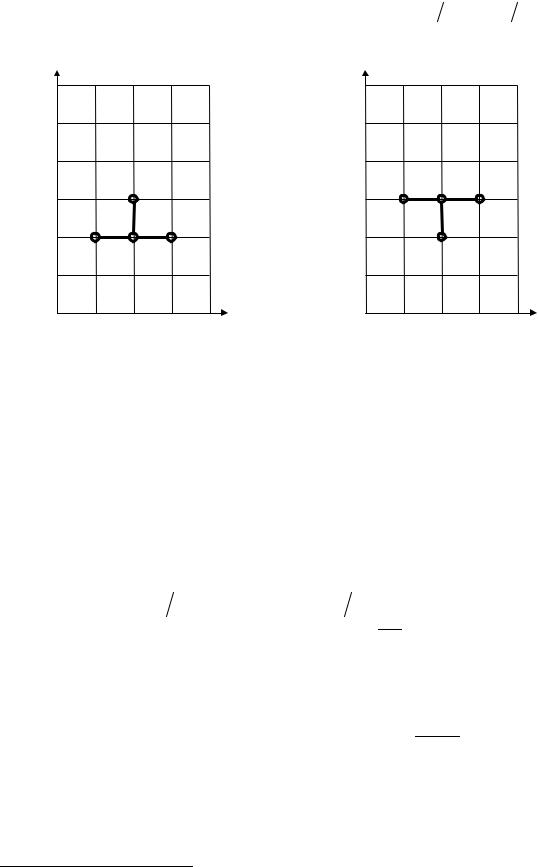
Для построения разностного аналога дифференциального уравнения (10.2) в частных производных используется сеточная область (рис. 10.1):
|
Ω ={(ti , xj ) |
|
ti = τi, i = |
|
; xj = hj, j = |
|
}, τ =T m, h = L n. |
|
0,m |
0,n |
|
|
|
t |
|
|
|
|
t |
|
|
|
Ω |
i + 1 |
i + 1 |
i |
i |
x |
x |
j – 1 j j + 1 |
j – 1 j j + 1 |
а |
б |
Рис. 10.1. Шаблоны для построения разностных аналогов производных
Для дифференциального уравнения (10.2) используются разностные аналоги первой и второй производных (см. рис. 10.1, а):
θ′t ≈ (θij+1 − θij )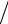 τ,
τ,
θ′xx′ ≈ (θij+1 − 2θij + θij−1 )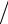 h2.
h2.
Во всех внутренних узлах области Ω дифференциальное уравнение заменяется разностным аналогом:
(θij+1 − θij ) τ − η(θij+1 − 2θij + θij−1 ) h2 = 0. |
(10.16) |
Если для i-го временного слоя решение θij , j = 0,n известно (например, для i = 0 известно распределение функции θ(0, x)= Θ(x) – начальное условие), то из
выражения (10.16) можно определить все узловые значения искомой функции для i + 1 слоя1:
θij+1 = θij + τη(θij+1 − 2θij + θij−1 )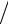 h2 , j =1,n −1.
h2 , j =1,n −1.
Значения θi0+1 и θin+1 на концах отрезка определяются из граничных усло-
вий (10.4):
1 Разностная схема в этом случае называется явной.




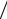











 ρ
ρ ρ >
ρ > 

 T
T  X
X 

 L
L L
L
 τ
τ