
Методы вычислительной математики
..pdf
1. Случай det(Am−1 ) ≠ 0 . Формируется матрица преобразования
P |
0 |
|
|
Pm = |
m−1 |
{ } |
|
|
0 |
1 |
|
и строится новая матрица |
|
|
|
|
* |
Pm−1 Am−1 |
Pm−1 {am−1} |
||
Am = Pm Am |
= |
a |
a |
. |
|
|
m−1 |
m m |
|
В силу сделанного предположения все угловые миноры матрицы Pm−1 Am−1 |
||||
отличны от нуля; последний |
угловой |
минор |
также отличен от нуля, |
|
m= det(Am ) = det(A) ≠ 0 . В рассмотренном частном случае теорема доказана.
2.Пусть теперь det(Am−1 ) = 0 . Разложение определителя матрицы А представляется в виде разложения по последнему столбцу:
det(A) = det(Am ) = ±a1m det(Am(1−)1 ) ± a2m det(Am(2−)1 ) ±…± amm det(Am(m−1) ) .
В силу того, что det(A) ≠ 0, существует хотя бы один det(A(k ) |
) ≠ 0 . Поме- |
m−1 |
|
няв местами строки матрицы А с номерами m и k ( m ≠ k в силу принятого усло-
вия |
det(Am−1 ) = 0 ), можно в результате |
получить преобразованную матрицу |
|||
A* |
= P A |
, у которой угловой минор |
* |
= det(A* |
) отличен от нуля. Те- |
m |
m−1 m−1 |
|
m−1 |
m−1 |
|
перь, в соответствии с доказательством случая 1, уже все угловые миноры матрицы Am* отличны от нуля.
Следствие. Если det(A) ≠ 0 , то существует матрица перестановок Р такая, что справедливо разложение
PA = LU ,
где L – нижняя треугольная матрица с ненулевыми коэффициентами на главной диагонали, U – верхняя треугольная матрица с единицами на главной диагонали.
Определение числа операций метода Гаусса
Для подсчета числа арифметических операций, необходимых для реализации алгоритма метода Гаусса, рассматриваются только операции умножения и деления как наиболее длительные при вычислениях на ЭВМ.
1. Вычисление коэффициентов ci j , i =1,m, j = i +1,m (сумма членов
арифметической прогрессии):
(m −1) + (m − 2) +…+ 1 = m(m −1) 2 .
2 .
41

2. Вычисление коэффициентов ai(kj ) , k = 2,m, i, j = k,m , (сумма слагае-
мых арифметической прогрессии 2-го порядка [5]):
(m −1)(m −1) + (m − 2)(m − 2) +…+11 = m(m −1)(2m −1)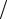 6 . 3. Вычисление значений fi(k ) , k = 2,m, i = k,m :
6 . 3. Вычисление значений fi(k ) , k = 2,m, i = k,m :
(m −1)+ (m − 2)+…+1 = m(m −1)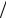 2 .
2 .
4.Вычисление значений yi , i =1,m производится m раз.
5.Вычисление xi , i =1,m при «обратном ходе» метода Гаусса:
1 + 2 +…+ (m −1)= m(m −1)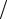 2 .
2 .
Общее количество операций умножения и деления определяется суммой всех указанных операций:
m + 3m(m −1)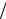 2 + m(m −1)(2m −1)
2 + m(m −1)(2m −1)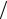 6 = m(m3 + 3m −1)
6 = m(m3 + 3m −1)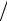 3 .
3 .
Количество операций умножения и деления приблизительно пропорционально m3 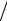 3, что и определяет затраты на выполнение метода Гаусса.
3, что и определяет затраты на выполнение метода Гаусса.
Вычисление определителя матрицы
Вычитание строк в методе Гаусса (образование линейных комбинаций уравнений) не изменяет значения определителя матрицы [9]. Знак определителя может измениться лишь при использовании процедуры выбора «главного» элемента, когда производится перестановка строк (столбцов) преобразуемой матрицы. После выполнения прямого хода метода Гаусса определитель исходной матрицы может быть вычислен перемножением элементов главной диагонали:
m
det(A)= det(LU ) = det(L)det(U ) = det(L) = ∏a(jjj−1) .
j=1
Здесь учтено, что L и U – треугольные матрицы и, кроме того, матрица U содержит только единицы на главной диагонали. Сохраняя значения коэффициентов, расположенных после преобразования уравнений (до операции деления коэффициентов строки на первый ненулевой элемент) на главной диагонали, можно вычислить определитель исходной матрицы.
Построение обратной матрицы
Пусть αpq , p,q =1,m – коэффициенты обратной матрицы A−1 . Согласно определению
42

|
|
|
|
|
|
i = j |
|
|
|
|
|
|
|
|
m |
|
|
1, |
– символ Кронекера1, |
|
|
||||
|
|
∑aik αk j = δi j , |
δi j = |
i ≠ j |
|
|
||||||
|
|
k=1 |
|
|
0, |
|
|
|
|
|
|
|
или, в компонентной форме, |
|
|
|
|
|
|
|
|
||||
a11 |
a12 |
a13 |
… a1m |
α11 |
α12 |
α13 |
|
… α1m |
|
1 0 0 … 0 |
||
|
|
|
|
|
α22 |
α23 |
|
|
|
|
|
|
a21 |
a22 |
a23 |
… a2m |
α21 |
|
… α2m |
0 1 0 |
… 0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a31 |
a32 |
a33 |
… a3m |
α31 |
α32 |
α33 |
|
… α3m |
|
= 0 0 1 |
… |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
… |
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
am2 |
am3 |
… amm |
|
αm2 |
αm3 |
|
|
|
… |
|
|
am1 |
αm1 |
… αmm |
0 0 0 |
1 |
||||||||
Теперь 1-й столбец обратной матрицы можно рассматривать как результат решения системы линейных алгебраических уравнений вида
a11 |
a12 |
a13 |
… a1m |
α11 |
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 |
a23 |
… a2m α21 |
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
a31 |
a32 |
a33 |
… |
a3m |
|
|
|
0 |
|
, |
α31 |
|
= |
|
|||||||
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
… |
|
… |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
am2 |
am3 |
… |
|
|
|
|
0 |
|
|
am1 |
amm αm1 |
|
|
|
|
|||||
2-й столбец обратной матрицы – результат решения системы линейных алгебраических уравнений
a11 |
a12 |
a13 |
… a1m |
α12 |
|
0 |
|
|
|||
|
|
|
|
|
|
α22 |
|
|
|
|
|
a21 |
a22 |
a23 |
… a2m |
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
a31 |
a32 |
a33 |
… |
a3m |
|
α32 |
|
|
0 |
|
, |
|
|
= |
|
||||||||
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
… |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
am2 |
am3 |
… |
|
|
|
|
|
0 |
|
|
am1 |
amm αm2 |
|
|
|
|
||||||
и так далее. Для нахождения всей обратной матрицы необходимо решить m систем линейных алгебраических уравнений с правыми частями, определенными специальным образом. При этом матрицу коэффициентов можно преобразовать лишь один раз, но одновременно преобразовывая m правых частей всех систем уравнений.
1 Кронекер Леопольд [7.12.1823 – 29.12.1891] – немецкий математик. С 1861 года – член Берлинской академии наук; с 1872 года стал членом-корреспондентом Петербургской академии наук. В 1883 году занял должность профессора Берлинского университета.
43

2.3.2. Метод квадратного корня
Метод квадратного корня используется для решения систем линейных алгебраических уравнений вида Ax = f с симметричной матрицей коэффициен-
тов ai j = a ji , i, j =1,m и основан на разложении матрицы коэффициентов А в произведение трех матриц
A = ST DS , |
(2.10) |
где S – верхняя треугольная матрица с положительными значениями на главной диагонали; D – диагональная матрица со значениями +1 или –1.
Согласно теореме 2.2 при неравенстве нулю всех угловых миноров матрицу А можно разложить в произведение A = LU . Нижняя треугольная матрица L с ненулевыми коэффициентами на главной диагонали может быть представлена в виде произведения NK , где N – нижняя треугольная матрица с единицами на главной диагонали, K – диагональная матрица, причем kii = λii , i =1,m :
λ
λ
L = λ
λ
11 |
0 |
0 |
21 |
λ22 |
0 |
31 |
λ32 |
λ |
m1 |
λm2 |
λ |
|
0 |
|
|
|
0 |
|
0 |
|
0 |
|
λ |
11 |
0 |
0 |
0 |
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
λ22 |
|
|
|||
|
0 |
|
n21 |
1 |
|
0 |
|
0 0 |
|
0 |
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
0 |
|
= n31 |
n32 |
1 |
|
0 0 |
|
0 |
λ33 |
0 |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m3 |
λ |
|
n |
m1 |
n |
m2 |
n |
m3 |
1 |
0 |
|
0 |
0 |
λ |
|
|
|
mm |
|
|
|
|
|
|
|
|
|
|
mm |
||||
После перемножения матриц N и K получается система линейных алгеб-
раических уравнений относительно величин ni j , |
i = |
|
, j = |
|
|
|
|
|||||||
2,m |
1,m −1: |
|||||||||||||
|
λ2 1 = n2 1λ11; |
|
|
|
|
|
|
|
|
|
|
|||
|
|
= n31λ11, λ3 2 = n3 2λ2 2 ; |
|
|
|
|
|
|
|
|||||
|
λ31 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ4 1 = n4 1λ11, λ4 2 = n4 2λ2 2 , λ4 3 = n4 3λ3 3; |
|||||||||||||
|
……………………………………………. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что |
n21 = λ21 |
λ11 , |
n31 = λ31 λ11 , |
n32 = λ32 λ22 , …. С учетом |
||||||||||
этого коэффициенты ni j |
и ki j |
матриц N и K можно представить в виде |
||||||||||||
λi j |
j < i |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
, |
|
|
|
|
|
|
|
|||||
λ j j |
|
|
|
λii , |
j = i |
|
|
|||||||
|
|
|
|
|
|
|
||||||||
|
|
j = i , |
i = |
2,m ; |
|
|
, i =1,m . |
|||||||
ni j = 1, |
ki j = |
|
||||||||||||
|
|
|
|
|
|
|
0, |
j ≠ i |
||||||
|
|
j > i |
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь матрицу А можно представить разложением
44
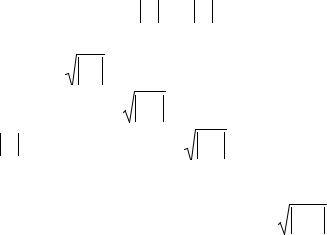
|
A = NKU. |
|
(2.11) |
|
Благодаря симметрии матрицы А имеет место равенство AT |
= A , что по- |
|||
зволяет произвести следующие преобразования: |
|
|
||
|
U T K T N T = NKU , |
|
|
|
|
U T K T = NKU (N T )−1 , |
|
|
|
|
N −1U T K T = KU (N T )−1 , |
|
||
|
K −1 N −1U T K T = U (N T )−1 . |
|
||
В |
силу того, что K −1, K T |
являются |
диагональными |
матрицами, |
N −1, |
U T – нижними треугольными, |
U , (N T )−1 |
– верхними треугольными, |
|
в левой части последнего равенства находится нижняя треугольная матрица, а в правой части – верхняя треугольная. Равенство возможно лишь при условии, что и в левой, и в правой частях этого тождества расположены диагональные матрицы.
Матрицы (N T )−1 и U имеют единицы на главной диагонали; следователь-
но, их произведение также содержит главную диагональ из единиц,
U (N T )−1 = E, U = N T .
Отсюда следует, что соотношение (2.11) можно переписать в виде
A = NKN T .
Далее, матрица K представляется в виде
K = K 1/ 2 D K 1/ 2 ,
где использованы следующие обозначения:
|
λ |
|
0 |
0 |
|
|
|
11 |
|
|
|
0 |
|
|
λ22 |
0 |
|
|
|
|
|
|
|
K 1/ 2 = 0 |
|
|
0 |
λ |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0 |
|
|
|
||
|
|
|
|
|
|
sign(λ11) |
0 |
0 |
|
|
0 |
sign(λ2 2 ) |
0 |
|
|||
D = |
0 |
0 |
sign(λ3 3 ) |
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|||
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λmm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
. |
|
|
|
|
|
|
sign(λ |
|
|
|
|
m m |
) |
||
|
|
|
|
|
45

Сравнивая соотношение
A = (N K 1/ 2 )D (K 1/ 2 N T )
с формулой (2.10), можно получить для матрицы S выражение S = K 1/ 2 N T , тоесть
верхнюю треугольную матрицу с положительными элементами на главной диагонали. Такимобразом, конструктивнопоказаносуществованиеразложения(2.10).
Вводятся обозначения: y = Sx, z = DSx , тогда алгоритм метода квадратного корня ST [D(Sx)]= f можно рассматривать как последовательность трех процессов:
1) ST z = f – вычисление решения z системы уравнений с нижней треугольной матрицей;
2) Dy = z – вычисление решения y системы уравнений с диагональной матрицей;
3) Sx = y – определение искомого решения x из системы уравнений с верхней треугольной матрицей.
Возможность разложения вида (2.10) рассматривается на примере симметричной матрицы третьего ранга:
a11
A= a21a31
ST DS
a |
a |
|
|
12 |
13 |
|
|
a22 |
a23 |
|
|
, |
|||
a32 |
a33 |
|
|
|
|
||
s |
0 |
||
|
11 |
|
|
= s |
s |
|
|
|
12 |
|
22 |
s |
s |
23 |
|
|
13 |
|
|
s11d11
=s12d11s13d11
s |
s |
s |
|
d |
|
0 |
0 |
|
|
|||||
|
11 |
|
12 |
|
13 |
|
|
|
11 |
|
|
|
|
|
S = |
0 |
s |
22 |
s |
23 |
, D = |
0 |
d |
22 |
0 |
|
; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
0 s33 |
|
|
0 |
0 |
|
|
|
|||||
|
|
|
d33 |
|
||||||||||
|
|
0 |
d |
|
0 |
|
0 |
s |
|
s |
|
s |
|
||||||||
|
|
|
|
|
|
11 |
|
|
|
|
|
11 |
|
|
|
12 |
|
13 |
|
||
|
|
0 |
|
0 d |
22 |
0 |
|
0 s |
22 |
s |
23 |
= |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
0 |
0 |
|
d33 |
|
0 |
|
|
0 |
|
|
|
|
||||
|
s33 |
|
|
|
|
|
s33 |
||||||||||||||
|
0 |
|
|
|
0 |
|
|
s |
s |
|
s |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
11 |
|
12 |
|
|
13 |
|
= |
|
|
|
|
s |
22 |
d |
22 |
|
0 |
|
|
|
0 |
s |
22 |
|
s |
23 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
s23d22 |
|
|
|
|
|
0 |
0 |
|
s33 |
|
|
|
|
|
|||||||
s33d33 |
|
|
|
|
|
|
|
||||||||||||||
|
s2 d |
|
|
|
|
s s d |
|
|
|
|
|
|
|
|
s s d |
|
|
|
|
|
|
|
|
|||||||||
|
11 |
11 |
|
|
|
|
11 |
12 |
|
11 |
|
|
|
|
|
|
|
11 |
|
13 |
|
|
11 |
|
|
|
|
|
||||
= s s d |
|
|
s2 d |
|
+ s2 |
d |
|
|
|
s s d |
|
+ s |
|
|
|
s |
|
d |
|
|
. |
|||||||||||
|
11 |
12 |
|
11 |
|
12 |
|
11 |
|
22 |
|
|
22 |
|
12 |
13 |
11 |
|
|
|
22 |
|
23 |
|
22 |
|
||||||
s s d |
11 |
s s d |
11 |
+ s |
22 |
s |
23 |
d |
22 |
s2 d |
11 |
+ s2 |
|
d |
22 |
+ s2 |
d |
33 |
|
|||||||||||||
|
11 |
13 |
|
12 |
13 |
|
|
|
|
13 |
|
23 |
|
|
|
|
33 |
|
|
|||||||||||||
46

В предложении, |
что |
|
d |
|
|
= sign(a ) , |
|
из уравнения |
a |
= s2 d |
11 |
получается |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
11 |
|
11 |
|
|||
|
|
|
|
= s11s12d11 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
s11 = a11 . Далее, из уравнения a12 |
|
определяется |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
s12 = a12 |
|
|
d11s11 = a12 |
d11 |
|
|
. |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
|
|
|
|
|
|||||||||||||||||||||
В силу условия det(A) ≠ 0 |
|
и теоремы 2.3 следует, что a11 ≠ 0. Используя |
|||||||||||||||||||||||||||||||||||||
уравнения a |
= s |
|
s |
|
d |
11 |
и a |
22 |
= s |
2 |
d |
11 |
+ s2 d |
22 |
, можно вычислить |
|
|
||||||||||||||||||||||
13 |
11 |
13 |
|
|
|
|
|
|
|
12 |
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
s13 = a13 |
|
d11s11 = a13 |
d11 |
|
a11 |
, |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 |
|
d |
22 |
= a |
22 |
− s2 |
d |
11 |
. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Поскольку d2 2 = sign (a2 2 − s122d11 ) |
, определяется значение |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
s |
22 |
= a |
22 |
− d |
11 |
a2 |
|
|
d |
2 |
a = |
|
(a a |
22 |
− a2 |
) a |
|
, |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
11 |
11 |
|
|
|
|
11 |
|
12 |
11 |
|
|
|
|||||||||||||
причем s22 ≠ 0 в силу условия |
|
|
2 |
|
≠ 0 . Далее из уравнения |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a23 = s12 s13d11 + s22 s23d22 |
|
|
|
|
|
|
|
||||||||||||||||||||
находится коэффициент
s23 = (a23 − s12 s13d11 )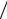 d22 s22 .
d22 s22 .
Из последнего уравнения
a33 = s132 d11 + s232 d22 + s332 d33 ,
определяются
d33 = sign(a33 − s132 d11 − s232 d22 ),
s33 = 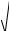 a33 − s132 d11 − s232 d22 .
a33 − s132 d11 − s232 d22 .
Нетрудно убедиться, что s33 ≠ 0 . Далее рассматривается процедура построения матриц S и D для произвольного числа уравнений m. Верхняя треугольная матрица S= [si j ] по определению имеет нулевые элементы:
si j |
= 0 при i > j. |
|
(2.12) |
|
Диагональная матрица D может быть определена формально с использова- |
||||
нием символа Кронекера D = [di j ] |
= [± δi j ]. |
Подсчитывается результат пере- |
||
множения матриц: |
|
= ∑± δik skj = [dii sij ], |
||
DS = ∑dik skj |
||||
m |
|
m |
|
|
k=1 |
|
k=1 |
|
|
|
m |
|
m |
|
A = ST DS |
= ∑sikT dkk skj = ∑ski dkk skj . |
|||
|
k=1 |
|
k=1 |
|
Из последнего выражения, с учетом соотношения (2.12), получается система линейных алгебраических уравнений:
47

i |
i−1 |
||
ai j = ∑ski dkk sk j = sii dii si j + ∑ski dkk sk j , i ≤ j = |
|
. |
|
1,m |
|||
k=1 |
k=1 |
||
Отсюда, при i = j, получаются соотношения
j−1
a j j = s2j j d j j + ∑sk2 j dkk , j =1,m k =1
для вычисления диагональных значений матриц D и S:
|
j−1 |
|
d j j = sign aj j − ∑sk2 j dk k , |
||
|
k =1 |
|
j−1 |
|
|
s j j = a j j − ∑sk2 j dkk , j = 1,m . |
||
k=1 |
|
|
«Наддиагональные» элементы матрицы S определяются по формулам
|
i−1 |
|
|
|
|
||||
si j = ai j − ∑ski dkk sk j sii dii , i < j = 2,m . |
||||
|
k =1 |
|
||
Определение числа операций метода квадратного корня
Число операций умножения, деления и извлечения квадратного корня, необходимых для реализации алгоритма рассматриваемого метода, подсчитывается в три этапа:
1. Факторизация исходной матрицы – формирование матриц S и D: m(m −1) 2 + m(m2 −1)
2 + m(m2 −1)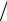 6 .
6 .
2. Выполнение «обратного» хода:
m(m −1) 2 + m .
2 + m .
3. Вычисление m значений квадратных корней.
Общееколичествооперацийравно m(m2 + 9m + 2)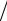 6, илиприблизительно m3
6, илиприблизительно m3 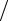 6 ,
6 ,
чтопрактическивдваразаменьше, чемчислооперацийвалгоритмеметодаГаусса. Пример 2.2. Решить систему двух линейных алгебраических уравнений
0,780x + 0,717 y = 0,063;0,717x + 0,659 y = 0,058
методом квадратного корня.
s11 =  a11 = 0,88318; d11 = 1; s12 = a12 s11d11 = 0,81184;
a11 = 0,88318; d11 = 1; s12 = a12 s11d11 = 0,81184;
s |
22 |
= |
a |
22 |
− s2 d |
11 |
= 0,0094054; |
d |
22 |
|
= −1; |
|
|
|
|
|
|
|
||||
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
T |
|
|
0,88318 |
0 |
z1 |
|
0,063 |
z1 |
|
|
0,071333 |
|
|||||||
1. |
S |
z = f , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||
|
|
|
|
|
|
|
= |
, |
|
= |
|
|||||||||||
|
|
|
|
|
|
0,81184 |
0,00941 |
z |
2 |
|
0,058 |
z |
2 |
|
0,0094054 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
48

1 |
0 y1 |
|
z1 |
|
y1 |
|
z1 |
|
|
0,071333 |
|
|
||||||||||||
2. Dy = z, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
= , |
= |
|
= |
|
|
|
|
||||||||||||||||
0 |
−1 |
y |
2 |
|
z |
|
|
|
y |
2 |
|
z |
|
− 0,0094054 |
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||
0,88318 |
|
0,81184 |
x1 |
|
y1 |
|
x1 |
|
1,000025 |
|
||||||||||||||
3. Sx = y, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
= , |
|
= |
|
. |
|||||||||||
|
0,0094054 |
x |
2 |
|
y |
2 |
|
x |
2 |
|
−1,000008 |
|||||||||||||
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1,0 |
|
|
|
|
|
|
|
|
|
||||||||
Точное решение задачи: |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x |
2 |
|
|
−1,0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2.4. Итерационные методы решения систем линейных алгебраических уравнений
Итерационными называются методы, в которых по некоторому начальному решению строится последовательность приближений искомого решения (в данном случае – решения системы линейных алгебраических уравнений (2.1)), причем при вычислении очередного приближения используется значение, полученное на предыдущем шаге вычислительного процесса. Иными словами, решение задачи полу-
чается как предел некоторой сходящейся последовательности приближений.
Как и ранее, рассматривается система линейных алгебраических уравнений с отличным от нуля определителем, det(A)≠ 0 , которая представляется
в компонентной форме:
m
∑ai j x j = fi , i = 1, m .
j=1
Эту систему уравнений можно преобразовать к виду
i−1 |
m |
∑aij x j + aii xi + |
∑aij x j = fi , |
j=1 |
j=i+1 |
|
i−1 |
|
|
xi = fi − ∑aij x j |
|
|
j=1 |
m |
|
|
|
|
|
|
|
||
|
|
aii , i = 1,m . |
||
− ∑aij x j |
||||
j=i+1 |
|
|
|
|
2.4.1. Метод Якоби1
Последнее выражение представляется в виде итерационной схемы Якоби:
(s+1) |
|
i−1 |
m |
|
|
|
|
(s) |
(s) |
aii , aii ≠ 0, i = 1,m , |
(2.13) |
||
xi |
= fi − ∑ai j x j |
− ∑ai j x j |
|
|||
|
|
j=1 |
j=i+1 |
|
|
|
где s – номер итерации. Для получения решения используется следующий алгоритм. В качестве нулевого приближения выбираются какие-либо (зачастую
1 Якоби Карл Густав Якоб [10.2.1804 – 18.2.1851] – немецкий математик. С 1830 года являлся иностранным членом-корреспондентом (с 1833 года – иностранным почетным членом) Петербургской академии наук; с 1836 года – членом Берлинской академии наук; с 1846 года – членом Парижской академии наук; с 1833 года – членом Лондонского королевского общества. С 1829 по 1942 годы был профессором Кенигсбергского университета.
49

произвольные) значения x(j0) , j =1,m , искомых величин, которые подставля-
ются в правую часть выражения (2.13), что позволяет определить первое приближение неизвестных x(j1) , j =1,m. Затем полученный результат вновь под-
ставляется в правую часть выражения (2.13) и вычисляются x(j2) , j =1,m , и так далее. Вычислительный процесс заканчивается, когда выполняется условие
max x(js+1) − x(js ) < ε,
1≤ j≤m
где ε > 0 – заданная погрешность вычисления результата.
Пример 2.3. Решить систему линейных алгебраических уравнений
4x1 + 2x2 = 5,3x1 + 5x2 = 9.
итерационным методом Якоби.
Точное решение этой системы x1 = 0,5, x2 = 1,5.
Из первого уравнения определяется x1 – первая неизвестная величина,
x1 = (5 − 2x2 ) 4 ,
4 ,
из второго уравнения – неизвестная величина x2, x2 = (9 − 3x1 )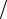 5.
5.
Полученные выражения записываются в виде итерационной схемы: |
||||
x(s+1) |
= (5 |
− 2x(s) ) 4, |
|
|
1 |
|
2 |
|
|
|
= (9 |
− 3x(s) ) 5. |
|
|
x(s+1) |
|
|
||
2 |
|
1 |
x(0) = 0, |
x(0) = 0. Ре- |
В качестве начального приближения принимаются |
||||
|
|
|
1 |
2 |
зультаты расчетов приведены в табл. 2.2. На рис. 2.3 отображен ход выполнения итерационного процесса Якоби.
|
x2 |
|
2 |
4x1 + 2 x2 = 5 |
|
|
|
|
1
3x1 + 5 x2 = 9
x1
0 
1 2 3
Рис. 2.3. Схема выполнения метода Якоби
50
