
Строительная механика зданий и сооружений. Спецкурс
.pdf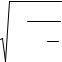
Откуда получаем |
|
|
|
|
|
||||
|
|
cosnl n sinnl |
r |
|
0 |
||||
или |
P |
||||||||
|
|
|
|
|
|
||||
EIc l |
|
|
|
|
|
||||
|
n |
|
|
ic |
|
|
|||
|
|
l |
|
tgnl 0 nl |
|
|
tgnl 0. |
||
|
|
3i |
3i |
|
|||||
|
|
|
|
|
|||||
|
|
p |
|
|
p |
|
|
||
Решение этого уравнения
n l 1 10,75ip . ic
Поскольку рама (см. рис. 3.5) будет состоять из г-образ- ных рам с жесткостью ригелей вдвое больше чем у нее самой (так как их длина вдвое меньше), то из любой многопролетной рамы с учетом вышесказанного получаем формулу для расчета критической силы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,75 |
|
|
|
|
EI |
|
|
|
n |
|
|
|
|
|
|
2 |
k |
|
|
||
Pкр |
|
1 |
|
|
|
|
|
|
, |
(3.3) |
||
|
|
2 ikр ikр 1 |
|
l2 |
|
|||||||
k 1 |
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ik |
|
|
|
|
|
|
|
|
где k – номер стойки или ригеля. Погонные жесткости ригеля суммируются только при жестком сопряжении ригеля с колонной;
ikс – погонная жесткость стойки;
ikp – погонная жесткость ригеля.
Проверим формулу (3.3), варьируя жесткость ригелей от нуля до бесконечности. Если жесткость ригеля равна бесконечности, то верхние узлы рамы закреплены от поворота, но имеют возможность перемещаться в горизонтальном направлении. Это соответствует стержню с двумя жесткими концами,
81

один из которых подвижен и для него справедлива формула Pкр 2 EIl2 . Если изгибная жесткость ригеля стремится к ну-
лю, то узлы рамы не воспринимают момент, стойка является консольной и для нее справедлива формула Pкр 14 2 EIl2 .
Подставляя жесткости ригеля в формулу (3.3), получим: при жесткости ригеля, равной бесконечности, Pкр 2 EIl2k , так
как |
0,75 |
|
= |
0,75 = 0. А при жесткости ригелей равной ну- |
||||||||||
|
р |
|
р |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
ik |
ik |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
iс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
лю, |
P |
1 |
2 |
EIk |
, так как |
|
0,75 |
= |
0,75 |
= 0,75, что соот- |
||||
4 |
|
|
|
iр iр |
1 0 |
|||||||||
|
кр |
|
|
l |
2 |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
k k |
|
|
|
||
|
|
|
|
|
|
|
|
|
iс |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
ветствует полученным ранее результатам для стержней с соответствующими концами.
Чтобы показать универсальность предложенной формулы (3.3) и метода, рассмотрим несколько примеров расчета многопролетных рам на устойчивость при действии вертикальной нагрузки. Значения погонных жесткостей элементов и распределение нагрузки примем произвольно.
Пример 3.1 (рис. 3.7)
iр1 = 1,5i, iр2 = 2i, i1 = 1i, i2 = 1,5i,
i3 = 2,5i, P1 = 0,15P, P2 = 0,3P, P3 = 0,55P.
Решая задачу методом перемещений и принимая высоту рамы равной единице, получим систему
уравнений: Рис. 3.7
82

3 ip1 4 ip2 4 i2 2 v2 Z1 + 2 ip2 Z2 + 6 i2 3 v2 Z3 = 0,2 ip2 Z1 + 4 ip2 4 i3 2 v3 Z2 + 6 i3 3 v3 Z3 = 0,
6 i2 3 v2 Z1+ 6 i3 3 v3 Z2 +
12 i2 2 v2 12 i3 2 v3 3 i1 1 v1 Z3 = 0,
где v  PEIкр l .
PEIкр l .
Раскрыв определитель и приравняв его к нулю, получим v = 2,1798, P1 = 4,75, P2 = 9,05, P3 = 17,42, Pкр 31,68 EIl2 .
Теперь решим эту же задачу предложенным выше методом, используя формулу (3.3). Жесткость первого ригеля на 2 умножать не надо, так как он имеет шарнирное крепление.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,75 |
|
|
|
|
|
|
0,75 |
|
|
|
|
EI |
|
|
P |
|
0,25 |
1,5 |
1 |
|
|
|
2,5 |
1 |
|
|
|
|
|
2 |
|
||||
|
1,5 2 2 |
|
|
|
|
2 |
2 |
|
l2 |
|||||||||||
кр |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1,5 |
|
2,5 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
32,45 EIl2 .
Как видно, результаты практически совпадают, погрешность составляет 2,4 %.
Необходимо отметить, что критическая сила, полученная в результате расчета, – это наименьшая сила, при которой рама примет новую форму равновесия. Но кроме того, существует местная потеря устойчивости, когда один или несколько сжатых элементов конструкции теряют устойчивость, а остальные остаются в первоначальном состоянии. Так, в примере 3.1 определим критическую силу из условия местной потери устойчивости левой сжатой стойки. В данном случае, поскольку остальная рама останется прямолинейной, то не будет происходить и линейное смещение ее верхних концов, значит,
83
стойка будет работать как стержень с одним жестким концом, а другим шарнирным. Поскольку по условию на левую стойку
приложено 0,15 от суммарной силы, то 0,15Pкр 2 (0,EI7l)2
20,14 EIl2 или Pкр 134,26 EIl2 . В данном примере критическая сила для рамы меньше, чем для стойки.
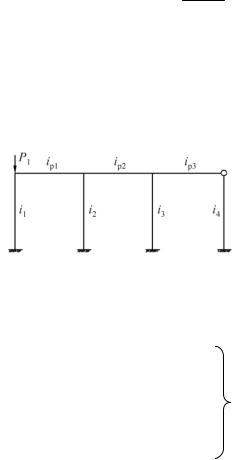
Пример 3.2. Найти силу, которую способна вынести рама до момента потери устойчивости (рис. 3.8).
iр1 = iр2 = iр3 = 2i, i1 = i2 = i3 = i4 = i.
Рис. 3.8
Решая задачу методом перемещений и принимая высоту рамы равной единице, получим
4 ip1 4 i1 2(v) Z1 + 2 ip1 Z2 + 0 + 6 i1 3(v) Z4 = 0,
2 ip1 Z1+ 4 ip1 4 ip2 4 i2 Z2 + 2 ip2 Z3+ 6 i2 Z4 = 0,
0 + 2 ip2 Z2 + 4 ip2 3 ip3 4 i3 Z3 + 6 i3 Z4 = 0,
6 i1 3(v) Z1 + 6 i2 Z2 + 6 i3 Z3 +
12 i1 1(v) 12 i2 12 i3 3 i4 Z4 = 0.
Раскрывая определитель и приравнивая его к нулю, полу-
чим v = 5,2949. Pкр 28,04 EIl2 .
Решая эту же задачу предложенным выше методом, используя формулу (3.3), получим
84

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,75 |
|
|
|
|
|
|
|
0,75 |
|
|
|
|||
P |
|
1 1 |
|
|
|
|
1 1 |
|
|
|
|
|
|
||||||||
|
|
|
2 2 |
|
|
|
2 (2 2) |
|
|||||||||||||
кр |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,75 |
|
|
|
|
|
|
|
|
|
EI |
|
|
|
EI . |
|||
1 1 |
|
|
|
|
|
|
0,25 1 |
2 |
= 28,71 |
||||||||||||
|
|
|
2 2 2 |
|
l2 |
|
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результаты расчета по двум методам получились достаточно близкими, погрешность вычислений 2,3 %. Если распределить силу P1 более равномерно между узлами рамы, погрешность снизится.
Проверим местную устойчивость стержня.
Pкр 4 2 5lEI2 197,4 EIl2 , что больше критической силы
для рамы.
При расчете многоэтажных рам устойчивость всей конструкции определяется устойчивостью нижнего этажа. В случае, если на каждый этаж рамы действует одна и та же нагрузка, следует использовать следующую формулу для определения общей критической силы, которая аналогична формуле (3.3), но учитывает работу стоек вышележащих этажей, находящихся под нагрузкой.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
0,75 |
|
|
|
|
|
|
EIk . |
|
|
Pкр 1 |
|
|
|
|
|
|
|
2 |
(3.4) |
||||
|
2 iр iр |
|
|
||||||||||
k 1 |
|
|
|
|
|
l2 |
|
||||||
|
|
|
1 |
k |
k 1 |
|
|
|
|
|
|
||
|
|
m |
p |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
ikr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
r 1 |
r |
|
|
|
|
|
|
||
85
Пример 3.3. Определить суммарную критическую силу, которую может вынести рама (рис. 3.9) до момента потери устойчивости. Посмотреть, как изменится критическая сила в случае 12-этажной рамы. Сечение стоек 30 45, сечение ри-
гелей 30 65.
Рис. 3.9
Имеем следующие значения относительных погонных жесткостей: для стоек i, для крайних ригелей 2,06i, для центрального ригеля 4,81i.
Пользуясь формулой (3.4) для одноэтажной рамы,
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,75 |
|
|
|
|
|
|
|
|
|
0,75 |
|
|
|
EI |
|
||
P |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 2 |
|
||||||
|
|
|
|
2 2,06 |
|
|
|
|
|
2 (2,06 4,81) |
|
l2 |
||||||||||
кр |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
35,58 |
EI . |
|
|
|
|
(3.5) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
Для 12-этажной рамы вместо погонной жесткости стойки |
||||||||||||||||||||||
в соответствии с формулой (3.4) получаем |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
1 |
|
|
1 |
... |
1 |
|
|
|
|
1 |
|
|
|
|
(3.6) |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
i 3,1i. |
|
|
|
|
|||
|
|
|
|
|
|
11 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
12 |
|
|
|
|
|
||||||
86
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,75 |
|
|
|
|
|
|
0,75 |
|
|
|
|||
P |
1 |
|
|
|
|
1 |
|
|
|
|
|
||||||
|
2 |
2,06 |
|
|
|
2 (2,06 4,81) |
|
||||||||||
кр |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
3,1 |
|
3,1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 2 |
|
EI |
30,4 |
EI . |
|
|
(3.7) |
||||
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
l2 |
|
|
|
|
Как видно, с повышением этажности здания критическая нагрузка снижается, что говорит о более ранней возможности потери устойчивости. Но с каждым этажом (см. формулу (3.6)) снижение ее происходит все более незначительным образом. Также необходимо заметить, что разница между (3.5) и (3.7) составляет около 15 %. Сравнивая результаты расчета примера 3.3 с результатами расчета, выполненного в ПК «Лира», получено, что погрешность вычислений не превосходит 5 % по критической силе и соответственно 2 % по расчетной длине.
Как видно, предложенный метод расчета многопролетных многоэтажных рам на устойчивость обладает достаточно высокой точностью и малой трудоемкостью [9].
§ 3.2. Влияние податливости соединений на устойчивость рамы
В существующих методах расчета пока не в полной мере учитывается влияние податливости узловых сопряжений на совместную работу конструкций. Поэтому, как правило, расчет каркасных зданий производится по расчетным схемам с шарнирными или жесткими узлами сопряжения элементов, что не всегда адекватно отражает работу конструкции, в особенности для железобетона. Для стыков сборных элементов характерна повышенная деформативность вследствие смятия бетона по контактным поверхностям и трещинообразования, податливости сварных соединений арматуры и закладных деталей.
87
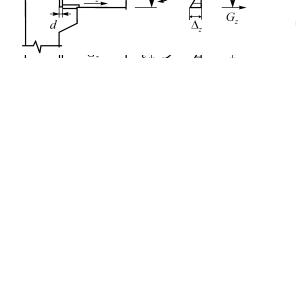
Рассмотрим П-образную железобетонную раму, длина пролета которой l = 6 м, высота колонн h = 3 м. Сечение ригеля и колонны возьмем из типового многоэтажного каркаса (рис. 3.10). Площадь сечения арматурного выпуска АN = 6 см2, рабочая высота сечения h0 = 42 см. Модуль упругости EN = = 21 МН/см2, жесткость опорной закладной детали при сдвиге
GZ =2,5 МН/см2.
Рис. 3.10
Для расчета рамы на устойчивость методом перемещений понадобится знать моменты по краям ригеля при повороте его конца на угол, равный единице.
Зададим угол поворота левого конца ригеля = 1. При этом левый конец его повернется на угол, отличный от единицы на какую-то величину, зависящую от жесткости стыка, которую обозначим 1 (рис. 3.11). Угол поворота правого конца обозначим 2.
88

Рис. 3.11 |
Рис. 3.12 |
|
Моменты по краям ригеля (рис. 3.12) можно записать сле- |
||
дующим образом: |
|
|
M1 1 1 c, |
M2 2 c, |
(3.8) |
где с – податливость соединения.
Используя дифференциальное уравнение изогнутой оси
стержня |
|
EIy M , подставляя в него уравнения (3.8) |
|
и гра- |
||||||||||||||||||||||||||||||||||||||||
ничные условия: y(0) = 0 и |
|
y(l) = 0, |
|
|
|
|
|
|
1 1 |
и |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
y |
(0) |
y (l) 2 , |
|||||||||||||||||||||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI M |
|
M |
|
|
|
|
|
l |
, |
|
|
|
|
|
|
EI M |
|
M |
|
|
l |
. |
||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
1 |
2 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
6 |
|
|||||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l c |
|
|
|
|
|
|
|
l c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
EI |
|
|
l |
|
c |
|
|
|
EI |
l |
|
c |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
(3.9) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l c |
|
|
|
|
|
|
|
|
l c |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
|
l c |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
EI |
|
|
c |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
||||||||
В соответствии с рекомендацией [10] примем |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
0.36 108 |
Н м. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
c |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
12 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
A |
|
E |
N |
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
N |
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
89 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

Подставляя конкретные значения параметров, получим
EIp 0,0029154 3 1010 0,875 108 Н м2,
EIk 0,0021333 3 1010 0,64 108Н м2,
|
iр 0,684ic. |
|
Тогда 1 0,419, |
2 0,130, и соответственно |
|
M1 (1 0,419) c 1,42iр, |
M 2 0,13,c 0,32iр. |
|
Решая задачу методом перемещений, т.е. составляя систему из трех трансцендентных уравнений, выражающих условие потери устойчивости, и приравнивая определитель к нулю, получаем
P 10 |
EIk |
. |
(3.10) |
кр |
l2 |
|
В случае абсолютно жесткого сопряжения ригеля с колонной имеем Pкр 13,3 EIl2k , т.е. результаты отличаются в 1,33 раза.
Решим данную задачу предложенным выше методом, т.е. используем для определения критической силы формулу (3.3). При абсолютно жестком соединении мы имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,75 |
|
|
EI |
|
|
EI |
|
P |
2 1 |
|
|
|
|
|
k = 13,48 |
|
|
k |
|
2 0,692 |
|
|
|
||||||
кр |
|
1 |
|
|
l2 |
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
и, соответственно, М1 = 4iр, а при сопряжении ригеля с колонной с учетом податливости соединения М1 = 1,42iр.
Как видно, в данном случае моменты отличаются в 2,82 раза. Для того чтобы это учесть, в формуле (3.3) нужно жесткость ригеля уменьшить в 2,82 раза.
90
