Строительная механика зданий и сооружений. Спецкурс

i2 02,EI6 h 4 EIh i0.

Параметры или аргументы функций влияния продольных сил:

71

§ 2.8. Расчет на устойчивость рам со ступенчатыми стойками

Как уже отмечалось выше, в промышленном строительстве широкое распространение получили рамы со ступенчатыми стойками.

Втаких рамах жесткое или шарнирное соединение ригеля

сколонной. Причем жесткое соединение встречается реже и осуществляется в металлических конструкциях путем крепления колонны к двум поясам фермы. Верхний и нижний пояс фермы находятся на достаточно большом расстоянии друг от друга (несколько метров), что создает значительный момент сопротивления изгибу, который пропорционален квадрату расстояния. Жесткость ригеля порой превосходит жесткость колонн более чем в десять раз. Таким образом, возможны два случая: шарнирное или жесткое крепление верхних концов стоек с абсолютно жестким ригелем.

Расчет устойчивости многопролетных рам при неодинаковом загружении стоек всегда приближенно можно привести к расчету однопролетной симметричной рамы при симметричном загружении стоек. Поэтому рассмотрим устойчивость однопролетных симметричных рам при симметричном загружении. Потеря устойчивости таких рам характеризуется линейным смещением ригелей и перекосом отдельных частей стоек.

При этом стойки рамы находятся в одинаковых условиях, а продольные силы в ригелях равны нулю. Учитывая это, можно рассмотреть устойчивость только одной стойки, принимая соответствующее условие закрепления верхнего конца этих стоек.

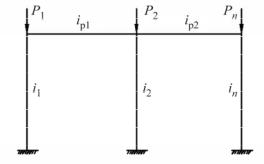
Пример 2.10. Определить критическую силу для рамы, представленной на рис. 2.28.

В этом случае применяем упрощенный метод перемещений. Поскольку на стойку действуют только продольные силы и она нигде не закреплена горизонтальными связями, эпюры

72

Верхний конец стойки подвижно защемлен. При потере устойчивости такой стойки концевые поперечные реакции в нижней и верхней ее частях равны нулю, т.е. H1 = H2 = 0.

По методу перемещений принимаем основную систему, показанную на рис. 2.29, б. Единичную эпюру моментов (рис. 2.29, в) относительно основной системы строим по табл. 2, п. 5 приложения, учитывая, что Z есть поворот дополнительной связи с учетом податливости узла.

В момент потери устойчивости должно быть r11 0. Это приводит к следующему уравнению критического состояния:

Вопросы для самоконтроля

1.Назовите преимущества метода перемещений для расчета стержневых систем.

2.Назовите методы решения ступенчатой стойки на устойчивость.

3.В чем отличие метода перемещений для ступенчатой стойки от метода перемещений для прямолинейной стойки?

4.Каковы отличия метода перемещений для расчета на прочность от метода перемещения для расчета на устойчивость?

5.Какие существуют упрощения расчета на устойчивость симметричных рам?

6.Какая форма потери устойчивости присуща симметричной раме?

74

ГЛАВА 3

§ 3.1. Приближенные способы расчета

Расчет на устойчивость рамных систем является актуальной задачей до сих пор, так как в современных программных комплексах этот вопрос проработан недостаточно, а ручной расчет получается чрезвычайно громоздким. Основная трудность заключается в решении системы трансцендентных уравнений, выражающих условие потери устойчивости. В данной главе предлагается новый подход расчета многоэтажных многопролетных рам без решения системы уравнений и без построения эпюр.

Рассмотрим 2-ролетную раму с жесткими узлами, представленную на рис. 3.1.

Рис. 3.1

Докажем вспомогательную лемму: принимая горизон-

тальное смещение ригеля рамы за единицу, при условии равновесия системы, получим сумму внутренних моментов в крайних сечениях стоек равной сумме внешних вертикальных сил.

Вырежем стойки рамы.

Из условия равновесия вырезанной части (сумма моментов относительно т. 1) (рис. 3.2) и с учетом того, что Н1 + Н2 + + H3 = 0, имеем

75

m

Mk P1 P2 ... Pn 1 P 1. (3.1)

k 1

Рис. 3.2

Докажем теорему: для многопролетных одноэтажных рам с постоянной высотой стоек, нагруженных вертикальной нагрузкой, значение критической силы остается неизменным при любом распределении нагрузки между стойками рамы.

Раму (рис. 3.1) загрузим произвольными силами, которые будем увеличивать до момента потери устойчивости системы. При достижении нагрузкой сил критического значения система будет находиться в состоянии безразличного равновесия, т.е. приращение потенциальной энергии должно быть равно нулю.

В момент потери устойчивости рама приобретет новую форму деформации (рис. 3.3). Подсчитаем работу внешних сил Р и внутренних моментов в крайних сечениях стоек; работу упругих сил в других сечениях рамы можно не учитывать, так как соответствующие этим силам деформации пренебрежимо малы. Составим уравнение равновесия в виде равенства нулю работ всех сил системы.

Работа внешних сил

n

Авнеш P1 P2 ... Pn Pi .

i 1

76

Рис. 3.3

Работа внутренних сил

n

Полученную критическую силу Pкр i 1Pi распределим иначе между стойками рамы. В этом новом нагружении мыс-

m

ленно передвинем ригель на единицу, тогда Mk не изменит-

k 1

ся (см. формулу (3.1)), работа внешних сил также останется постоянной. Реакции в наложенных связях также не совершают работы: моменты в жестких заделках равны нулю в силу равновесия узлов рамы, а реакция в шарнирной опоре

от распределения сил между узлами рамы. Следовательно, равенство (3.2) также будет соблюдаться. Значит, для перевода рамы из деформированного состояния в прямолинейное приращение потенциальной энергии будет равным нулю, что подтверждает теорему [16].

77

Но при доказательстве теоремы использовался ряд допущений (например, что все внешние силы совершают работу на одинаковом перемещении ). Необходимо посмотреть,

насколько велика погрешность таких предположений. Рассмотрим раму с шарнирно закрепленным ригелем,

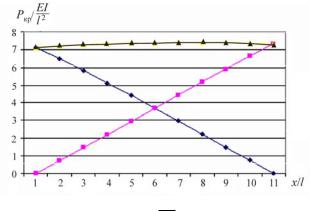
жесткость правой стойки которой вдвое больше жесткости левой стойки. Построим график зависимости критической нагрузки от ее положения на ригеле, понимая, что она распределится обратно пропорционально расстоянию до стоек.

Рис. 3.4: Ркр1 ;  Ркр2 ;  Ркр

По графику зависимости критической силы от ее положения (рис. 3.4) видно, что критическая нагрузка меняется от

не превышает 3,5 %.

Таким образом, для расчета рамы с постоянной высотой стоек на устойчивость рационально определять не критические нагрузки, приложенные в узлах, а обобщенную критическую силу, которую рама способна выдержать до потери устойчивости.

78

Точки, где эпюра моментов пересекает ось ригелей рамы, можно заменить шарнирами, так как в них момент равен нулю.

Поскольку вертикальное смещение этих точек пренебрежимо мало, то можно раму (рис. 3.5) разбить на отдельные рамы с шарнирно-подвижными опорами в точках А и В. При этом критическая сила найдется как сумма критических сил для от-

дельных рам. Если мысленно передвинуть эпюры на ригелях (при этом точки А и В также сменят свое местоположение), то передвинутся и эпюры на стойках. Вышеизложенные рассуждения позволяют сделать вывод, что критическая сила не зависит от положения точек А и В и на ригеле. Поэтому эти точки удобно располагать на середине ригеля.

Рассмотрим г-образную раму (рис. 3.6, а). Выберем основную систему метода перемещений (рис. 3.6, б). При повороте Z1 1 в ригеле возникнет момент, равный 3ip. Соответ-

ственно, расчет рамы (рис. 3.6, а) можно заменить расчетом стержня с упругоподатливой на изгиб опорой с жесткостью 3ip, свободной при этом от горизонтального перемещения

(рис. 3.6, в).

Рис. 3.6

79

Найдем критическую нагрузку статическим способом. Дифференциальное уравнение изгиба стержня можно за-

писать в виде

EIy M P( y) r

или

EIy Py P r .

Решение этого уравнения:

y A cos(nx) B sin(nx) Pr ,

где n EIP .

Для определения A, B, , имеем четыре граничных условия:

Получаем систему четырех однородных алгебраических уравнений. Поскольку нас интересует ненулевое решение для A, , , приравняем к нулю определитель, составленный из ко-

эффициентов при этих неизвестных.

80