Строительная механика зданий и сооружений. Спецкурс

Подставим граничные условия (4.6) в (4.5) и получим cos(kl) ch(kl) 1.

Это уравнение имеет бесконечное множество решений.

Тогда первые три частоты собственных колебаний будут

Первые три формы собственных колебаний представлены на рис. 4.1.

Задача сильно упростилась бы, если бы масса была не распределенной, а сосредоточенной в одной или нескольких дискретных точках. Силы инерции в этом случае могут находиться только в точках сосредоточения масс. Соответственно, ускорения и перемещения можно тоже искать только для этих точек.

Для приближенного решения многих динамических задач применяют метод приведения масс, при котором системы

сбольшим количеством степеней свободы сводятся к системе

смалым числом степеней свободы или для простых конструкций с одной степенью свободы. Для этого приведенные массы относят к определенным точкам, обычно по середине стержней. Приведенная масса должна быть такой, чтобы при ее введении собственная частота была равной частоте исходной конструкции. Очевидно, что в этом случае приведенная масса не будет равна непосредственно массе конструкции.

121

§ 4.4. Свободные колебания систем с одной степенью свободы

Если упругая система в результате взаимодействия с ка- ким-либо другим физическим телом оказывается выведенной из состояния равновесия, то после прекращения действия система будет совершать свободные колебания.

Свободные колебания системы с одной степенью свободы рассмотрим на примере балки, жестко заделанной одним концом

(рис. 4.4).

Под действием груза Q = mg точка его приложения переместится вниз на величину ycт.

При свободных колебаниях балки в любой мо-

мент времени на массу m, отклонившуюся от положения равновесия, будет действовать восстанавливающая сила R, т.е. сила упругой реакции балки, стремящаяся вернуть массу в положение статического равновесия и направленная в сторону этого положения. Восстанавливающая сила пропорциональна величине отклонения (y) точки, в которой сосредоточена масса,

т.е. R = ry.

Коэффициент пропорциональности r представляет собой реакцию балки в рассматриваемой точке при перемещении этой точки, равном единице. Очевидно, что r = 1/ , где – перемещение рассматриваемой точки, вызванное единичной

силой (так, при продольных колебаниях 1EFl , а при попе-

речных 1 l3 , см. рис. 4.4). 3EI

122

Число колебаний в минуту называется технической частотой и обозначается n. Техническая частота определяется по формуле

n 60T 30 60v .

График свободных колебаний представлен на рис. 4.5. Решение данной задачи свелось к определению переме-

щения в точке сосредоточения массы. Такое решение задачи намного проще, чем решение аналогичной балки, но с распределенной массой (см. рис. 4.1).

Поэтому в дальнейшем будем рассматривать задачи, в которых распределенные массы стержней сведены в точечные. При этом массы необходимо умножать на коэффициент приведения, т.е. отношение приведенной массы к полной массе конструкции.

Для практических целей часто бывает достаточно найти наименьшую частоту, представляющую наибольшую опасность в случае возможности возникновения резонанса, так как резонанс на этой частоте приводит к наибольшему динамическому эффекту.

Найдем приведенную массу для консольного стержня из условия равенства (4.9) и наименьшей частоты (4.7).

где mk – масса конструкции,

124

или mпр 3,5153 2 mk 0,244mk .

Для других условий закрепления концов балки приведенные массы равняются [4]:

• шарнирно опертая балка mпр 0,493mk , масса приво-

дится к середине пролета;

• балка с двумя жесткими концами mпр 0,385mk , масса приводится к середине пролета.

Пример 4.1. Определить круговую и техническую частоту, а также период собственных колебаний сосредоточенного груза Q = 12 кН, приложенного посредине ригеля рамы (рис. 4.6, а), пролет L = 6 м. Собственный вес конструкции не учитывается. Момент инерции поперечного сечения относи-

тельно горизонтальной оси I 2500см4. Принять в расчетах модуль упругости E 2,1 104 кН/см2.

а б

Рис. 4.6

Статический прогиб под грузом определяем по формуле yст 11 Q. Перемещение 11 от действия груза Q = 1 находим

путем перемножения эпюры моментов M (рис. 4.6, б) на себя, используя способ А.Н. Верещагина:

125

Период колебаний находим по формуле

T2 6,28 0,203с.

30,9

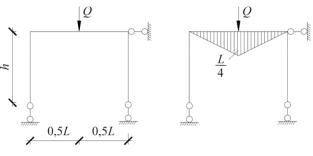
Пример 4.2. Требуется определить циклическую частоту свободных колебаний рамы, представленной на рис. 4.7.

Данная рама представляет собой систему с одной степенью свободы, т.к. масса на левой стойке (см. рис. 4.7, а) имеет возможность перемещаться только по горизонтальной оси.

– перемещение по направлению возможных колебаний груза массы m. Для этого необходимо построить эпюры моментов от единичной силы, приложенной в точке сосредоточения груза и направленной по направлению возможных колебаний рамы (см. рис. 4.7, б). Задача является статически неопределимой.

126

Наиболее рационально в данном случае построить эпюры методом сил, так как задача является один раз статически неопределимой, в отличие, например, от метода перемещения, для которого задача дважды неопределенна.

г д

Рис. 4.7

Основная система и единичная эпюра представлены на рис. 4.7, в, грузовая эпюра представлена на рис. 4.7, г. Составим основное уравнение метода сил.

Произведя перемножение эпюр по способу А.Н. Верещагина, найдем

127

Подставим найденные перемещения в (4.12) и найдем неизвестное усилие X1:

X1 вг 36 0,225. Найдя X1, построим оконча-

вв 160

тельную эпюру моментов (см. рис. 4.7, д) путем M д

Mг X1 Mв.

Для определения необходимо либо эпюру моментов (см. 4.7, д) умножить на саму себя, либо грузовую эпюру (см. рис. 4.7, г). Второй вариант предпочтителен.

Пример 4.3 (пример заимствован из книги [4, с. 139]). Требуется определить собственную частоту вертикальных колебаний фундамента (рис. 4.8), передающего равномерное давление на грунт, равнодействующая которого Q = 2 МН. Площадь подошвы фундамента составляет F = 10 м2, а коэффициент упругого сжатия грунта k = 25 кН/см3.

Рис. 4.8

128

Давление на грунт основания составляет q QF 200010 20кН/см2.

При таком давлении упругая статическая осадка фундамента, которая войдет в расчетную формулу для частоты вместо статического прогиба, будет равна

y qk 2025 0,8см.

§4.5. Свободные колебания систем со многими степенями свободы

Число возможных форм свободных колебаний упругой системы равно числу степеней ее свободы. Каждой форме колебаний соответствует своя частота. Совокупность частот данной системы составляет ее спектр частот.

Для практических целей часто бывает достаточно найти наименьшую частоту, представляющую наибольшую опасность. Низшую частоту иногда называют частотой основного тона колебаний. Следующий по порядку тон называют первым обертоном.

Для определения неизвестных частот можно составить выражения:

перемещения точек приложения сосредоточенных масс под действием сил инерции этих масс:

129