
Шведенко Начала математического анализа 2011
.pdf
131
8">09 >08x;(x 2 X) ^ (0<jx;aj< ) ) jf(x) ;bj<" ,
SOOTWETSTWENNO1, ISTINNYM, TOGDA KAK GOWORITX W DANNOJ SITUACII (KOGDA WBLIZI TO^KI a NET OTLI^NYH OT NEE TO^EK,
PRINADLEVA]IH MNOVESTWU X ) O PREDELE FUNKCII y = f(x) PRI x, STREMQ]EMSQ K a PO MNOVESTWU X , BESSMYSLENNO.
eSLI MNOVESTWO X, NA KOTOROM ZADANA FUNKCIQ y = f(x), SODERVIT CELIKOM NEKOTORU@ OKRESTNOSTX TO^KI a,2 TO PO-
NQTIQ PREDELA FUNKCII W TO^KE PO MNOVESTWU I PREDE-
LA FUNKCII W TO^KE W IZNA^ALXNOM OPREDELENII (SM. S. 101)
SOWPADA@T: |
lim f(x) = limf(x). |TO SLEDUET IZ TOGO, ^TO |
|
|
X3x!a |
x!a |
ESLI ^ISLO |
> 0 |
DOSTATO^NO MALO, TO WYPOLNENIE NERA- |
WENSTW 0 < jx ; aj < WLE^ET WYPOLNENIE USLOWIQ x 2 X, |
|||||||||||||||
A POTOMU FORMULY |
|
|
|
|
|
|
|
|
|
|
|||||
|
8">09 >08x (x 2 X) ^ (0<jx;aj< ) ) jf(x) ;bj<" |
||||||||||||||
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
I |
|
8">09 >;08x 0<jx;aj< ) jf(x) ;bj<" |
|
||||||||||||
|
|
||||||||||||||
OKAZYWA@TSQ RAWNOZNA^NYMI. |
|
|
|
|
|
|
|||||||||
|
pODOBNO \TOMU, ESLI MNOVESTWO X PREDSTAWLQET SOBOJ |
||||||||||||||
LEWU@ OKRESTNOSTX TO^KI a, |
TO lim f(x) = |
lim |
f(x), A ES- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
X3x!a |
|
x!a;0 |
|
|
|
LI W KA^ESTWE MNOVESTWA X WYSTUPAET PRAWAQ OKRESTNOSTX |
|||||||||||||||
TO^KI a, |
TO lim f(x) = |
lim f(x). |
|
|
|
|
|
||||||||
|
|
|
|
X3x!a |
|
|
x!a+0 |
|
|
|
|
|
|
||
|
tO^NO TAK VE, ESLI a = +1, A MNOVESTWO X SODERVIT |
||||||||||||||
PROMEVUTOK WIDA (c + |
1 |
), TO |
lim f(x) = |
lim f(x), A ESLI |
|||||||||||
a = ;1, |
|
|
|
|
|
X3x!a |
x!+1 |
|
|
|
|||||
I MNOVESTWO X |
SODERVIT PROMEVUTOK WIDA (;1 c), |
||||||||||||||
TO |
lim f(x) = |
lim f(x). |
|
|
|
|
|
|
|
||||||
|
X3x!a |
|
|
x!;1 |
|
|
|
|
|
|
|
|
|
|
|
|
eSLI a = +1, A X = N | MNOVESTWO NATURALXNYH ^ISEL, TO |
||||||||||||||
|
lim |
f(x) = |
lim |
f (n) ESTX PREDEL POSLEDOWATELXNOSTI |
f |
f(n) |
. |
||||||||
X3x!a |
|
n!+1 |
|
|
|
|
|
|
|
g |
|
||||
1 sOGLASNO PRAWILU ISTINNOSTI IMPLIKACII (SM. pRILOVENIE I).
2 iSKL@^AQ, WOZMOVNO, SAMU \TU TO^KU.

132
wOT KRITERIJ (\KWIWALENTNOE OPREDELENIE) \^EREZ POSLE-
DOWATELXNOSTI" PREDELA FUNKCII W TO^KE PO MNOVESTWU:
|
|
w PREDPOLOVENII, ^TO a | PREDELXNAQ TO^KA MNOVESTWA |
||||||||||||||||||||
|
|
X (NA KOTOROM ZADANA FUNKCIQ y = f(x)), WYPOLNENIE SOOT- |
||||||||||||||||||||
|
|
NO[ENIQ |
lim |
f(x) = b RAWNOSILXNO ISTINNOSTI UTWERV- |
||||||||||||||||||
|
|
|
|
|
|
|
|
: \ |
|
X3x!a |
|
|
|
|
1 |
|
fxng |
|
|
|||
|
|
DENIQ |
|
KAKOWA BY NI BYLA POSLEDOWATELXNOSTX |
|
|
TO^EK |
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
6 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
xn |
|
|
X xn |
|
=a, |
ESLI ONA IMEET PREDEL , RAWNYJ |
a, TO PO- |
|||||||||||||
|
|
SLEDOWATELXNOSTX |
ff(xn)g |
IMEET PREDEL , RAWNYJ b ". |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dOKAZATELXSTWO |
. |
pUSTX lim |
f(x) = b, T. E. ISTINNYM |
||||||||||||||||
QWLQETSQ UTWERVDENIE |
X3x!a |
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
6 |
||||||||||||||||||
|
|
|
|
|
f |
|
g |
|
|
|
; |
|
|
|
|
|
|
|||||
8">09 >0 |
8x (x 2 X)^(0<jx;aj |
< ) ) jf(x);bj |
<" ,2 |
( ) |
||||||||||||||||||
eSLI |
|
|
xn |
|
| L@BAQ POSLEDOWATELXNOSTX TO^EK xn |
|
X xn |
=a, |
||||||||||||||
DLQ KOTOROJ lim xn = a, TO KAKOWO BY NI BYLO ^ISLO ">0, DLQ SU]ESTWU@]EJ DLQ NEGO (W SILU UTWERVDENIQ ( ))
NOSTI TO^KI a SU]ESTWUET TAKOE NATURALXNOE ^ISLO n0 , ^TO
WSE TO^KI xn S \NOMERAMI" n > n0 |
POPADA@T W \TU OKREST- |
||||||
NOSTX, TAK ^TO (OPQTX W SILU UTWERVDENIQ ( )) jf(xn);bj<" |
|||||||
I, SLEDOWATELXNO, lim f(xn) = b. |
|
|
|
|
|
|
|
nAOBOROT, ESLI NE WERNO, ^TO |
lim |
f(x) = b, T. E. ISTINNO |
|||||
X |
3x!a |
|
|
|
|
|
|
OTRICANIE UTWERVDENIQ ( ) | UTWERVDENIE |
|
|
|||||
; |
|
2 |
|
3 |
|
|
|
9">08 >09x (x 2 X) ^ (0;aj< ) ^ (jf(x) ;bj>") ,3 |
|||||||
TO, BERQ ODNO ZA DRUGIM ZNA^ENIQ = 1 |
1 |
|
1 |
, : : : |
4 |
I ZAPISYWAQ |
|
|
|
|
|||||
x1 x2 x3 : : : SU]ESTWU@]IE DLQ NIH (SOGLASNO POSLEDNE- MU UTWERVDENI@) ZNA^ENIQ x, POLU^A@T POSLEDOWATELXNOSTX
fxng TO^EK xn 2 X xn 6=a, DLQ KOTOROJ lim xn = a, NO NE WER-
NO, ^TO lim f(xn) = b. Q.E.D.
1 kONE^NYJ ILI BESKONE^NYJ.
2 |
|
3 |
NA S. 130 EGO WARIANTAMI DLQ a = 1. |
3 s UKAZANNYMI W SNOSKE |
|
||
4 s ZAMENOJ PRI a = 1 |
NERAWENSTW 0<jx;aj< NA x>c ILI x<;c. |
||
sOOTWETSTWENNO, c = 1 |
2 3 : : : PRI a = 1. |
||

133
wERHNIJ I NIVNIJ PREDELY FUNKCII
pO ANALOGII S PONQTIQMI WERHNEGO I NIVNEGO PREDELOW POSLEDO- WATELXNOSTI (SM. S. 87) WWODQT PONQTIQ WERHNEGO I NIVNEGO PREDELOW FUNKCII y = f(x) W TO^KE a (WKL@^AQ SLU^AI a = 1, STREMLENIQ K TO^KE a SLEWA, SPRAWA ILI PO NEKOTOROMU MNOVESTWU X).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w ^ASTNOSTI, ZAPISX |
|
|
lim f(x) = b PO OPREDELENI@ OZNA^AET, ^TO: |
||||||||||||||
|
|
|
|
|
|
|
|
x!a+0 |
|
|
|
|
|||||
a) SU]ESTWUET POSLEDOWATELXNOSTX fxng TO^EK xn >a, DLQ KOTOROJ |
|||||||||||||||||
lim xn = a, A limf(xn) = b |
|
|
|
|
|
|
|
|
|||||||||
B) NE SU]ESTWUET POSLEDOWATELXNOSTI fxng TO^EK xn > a, DLQ KO- |
|||||||||||||||||
TOROJ lim xn = a, A limf (xn)>b, |
|
|
|
|
|||||||||||||
A ZAPISX |
|
lim |
|
f(x) = b OZNA^AET, ^TO: |
|
|
|
|
|||||||||
|
x!+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a) SU]ESTWUET POSLEDOWATELXNOSTXfxng, RASHODQ]AQSQ K +1, DLQ |
|||||||||||||||||
KOTOROJ |
limf(xn) = b |
|
|
|
|
|
|
|
|
|
|
||||||
B) NE SU]ESTWUET POSLEDOWATELXNOSTI fxng, RASHODQ]EJSQ K +1, |
|||||||||||||||||
DLQ KOTOROJ limf(xn)<b. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
|
sin |
1 |
= |
|
||||
nAPRIMER: |
|
lim |
sin |
= 1, A |
lim |
|
1. |
||||||||||
|
x |
|
|||||||||||||||
|
|
|
|
x!0 0 |
|
|
x!0 0 |
|
x |
; |
|||||||
uSLOWIE lim f(x) = lim f(x) = b NEOBHODIMO I DOSTATO^NO DLQ TOGO,
x!a x!a
^TOBY FUNKCIQ1 y =f(x) IMELA W TO^KE a PREDEL, RAWNYJ b.2
dOKAZATELXSTWO. eSLI lim f(x) = b, TO3 KAKOWA BY NI BYLA SHODQ]A-
x!a
QSQ K a POSLEDOWATELXNOSTX fxng TO^EK xn 6=a, SOOTWETSTWU@]AQ POSLE- |
|||||||||||||
DOWATELXNOSTX |
f |
f (xn) |
SHODITSQ K b, A POTOMU |
lim |
f (x) = limf (x) = b. |
||||||||
|
g |
|
|
|
|
|
|
|
x!a |
x!a |
|||
nAOBOROT, |
PUSTX \TI SOOTNO[ENIQ WYPOLNENY, NO DLQ NEKOTOROJ |
||||||||||||
POSLEDOWATELXNOSTI fxng TO^EK xn |
6=a, SHODQ]EJSQ K a, POSLEDOWATELX- |
||||||||||||
NOSTX ff(xn)g |
NE SHODITSQ K b, T.E. LIBO lim f(xn) = b 6=b, LIBO U |
||||||||||||
POSLEDOWATELXNOSTI ff(xn)g NET (NI KONE^NOGO, NI BESKONE^NOGO) PRE- |
|||||||||||||
DELA. wO WTOROM SLU^AE |
lim |
f(xn) 6=limf(xn), W SILU ^EGOeSU]ESTWOWUET |
|||||||||||
|
|
||||||||||||
PODPOSLEDOWATELXNOSTX fxnkg POSLEDOWATELXNOSTI fxng (TAKVE SHODQ- |
|||||||||||||
|
|
|
|
|
|
|
|
|
e |
|
|||
]EJSQ K a), DLQ KOTOROJ lim f(xnk) = b |
6=b. w OBOIH SLU^AQH WOZNIKAET |
||||||||||||
PROTIWORE^IE S TEM, ^TO |
lim |
f(x) = lim f(x) = b. Q.E.D. |
|||||||||||
|
|
|
|
x!a |
x!a |
|
|||||||
|
|
||||||||||||
1 zADANNAQ W OKRESTNOSTI TO^KI a (KROME, WOZMOVNO, EE SAMOJ). |
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
b = 1. |
3 uTWERVDENIE WERNO I DLQ a = 1 x ! a 0 |
|||||||||||||
w SILU KRITERIQ (\KWIWALENTNOGO OPREDELENIQ) PREDELA FUNKCII
\^EREZ POSLEDOWATELXNOSTI" (SM. S. 109).

134
III.6. ~TO NAZYWA@T KRITERIEM kO[I SU]ESTWOWANIQ PREDELA FUNKCII
kRITERIJ kO[I SU]ESTWOWANIQ PREDELA FUNKCII W TO^KE1. fUNKCIQ y = f(x) IMEET PREDEL2 W TO^KE a TOGDA
I TOLXKO TOGDA, KOGDA DLQ L@BOGO POLOVITELXNOGO ^ISLA " SU]ESTWUET OKRESTNOSTX TO^KI a, W KOTOROJ3 ZNA^ENIQ FUNKCII RAZNQTSQ MEVDU SOBOJ MENX[E, ^EM NA ":
9b;b = limf(x) () 8">09 >08x0 8x00;(0<jx0;aj< )^ x!a ^(0<jx00;aj< ) ) jf(x0);f(x00)j<" .4
dOKAZATELXSTWO. pUSTX PREDEL FUNKCII y = f(x) W TO^KE
a SU]ESTWUET I PUSTX limf(x) = b. wZQW L@BOE POLOVITELX-
x!a
NOE ^ISLO ", MOVNO UTWERVDATX, ^TO DLQ ^ISLA 2" (KAK I DLQ L@BOGO POLOVITELXNOGO ^ISLA) SU]ESTWUET TAKOE POLOVI- TELXNOE ^ISLO , ^TO DLQ L@BOGO ZNA^ENIQ x, UDOWLETWORQ- @]EGO NERAWENSTWAM 0<jx;aj< , WYPOLNQETSQ NERAWENSTWO jf(x);bj< 2" . pO\TOMU DLQ L@BYH DWUH TAKIH ZNA^ENIJ x0 x00
jf(x0);f(x00)j = jf(x0);f(x00) bj 6 jf(x0);bj+ jf(x00);bj<",
T. E. ISTINNO UTWERVDENIE
8">09 >08x0 8x00;(0<jx0;aj< )^(0<jx00;aj< ) )
) jf(x0);f(x00)j<" .
1 nA SAMOM DELE AWTOR \TOGO KRITERIQ (ANALOGA KRITERIQ kO[I SHO- DIMOSTI POSLEDOWATELXNOSTI) | NEMECKIJ MATEMATIK d@BUA-rEJMON
(Du Bois-Reymond Paul, 1831{1889), SFORMULIROWAW[IJ EGO W GL. V \oB]EJ TEORII FUNKCIJ" [36] KAK \oB]IJ PRINCIP SHODIMOSTI I RAS-
HODIMOSTI" (\Das allgemeine Convergenzund Divergenzprincip").
2 tERMIN PREDEL, NE SOPROWOVDAEMYJ PRILAGATELXNYM BESKONE^- NYJ, PODRAZUMEWAET KONE^NOE ^ISLO.
3 eSLI ISKL@^ITX IZ NEE SAMU TO^KU a.
4 wARIANTY KRITERIQ DLQ ODNOSTORONNIH PREDELOW DANY NA S. 136.

135
nAOBOROT, PUSTX \TO UTWERVDENIE ISTINNO, I DLQ PRO- IZWOLXNO WZQTOGO POLOVITELXNOGO ^ISLA " PUSTX | TO POLOVITELXNOE ^ISLO, KOTOROE (W SILU \TOGO UTWERVDENIQ) SU]ESTWUET DLQ \TOGO ^ISLA ". eSLI fxng | L@BAQ SHODQ- ]AQSQ K a POSLEDOWATELXNOSTX TO^EK xn 6=a, TO DLQ UKA- ZANNOGO ^ISLA (KAK I DLQ WSQKOGO POLOVITELXNOGO ^ISLA) SU]ESTWUET TAKOE ^ISLO n0, ^TO DLQ WSEH BOLX[IH EGO NATU- RALXNYH ^ISEL n m WYPOLNQETSQ NERAWENSTWO jxn ;xmj < , A SLEDOWATELXNO, I NERAWENSTWO jf(xn);f(xm)j<". |TO OZNA- ^AET, ^TO POSLEDOWATELXNOSTX ff(xn)g QWLQETSQ FUNDAMEN-
A POTOMU (W SILU KRITERIQ kO[I DLQ POSLEDOWATELXNOSTEJ) I SHODQ]EJSQ K NEKOTOROMU ^ISLU b. oSTAETSQ DOKAZATX, ^TO \TO ^ISLO b NA SAMOM DELE QWLQETSQ OB]IM PREDELOM WSEH TAKIH POSLEDOWATELXNOSTEJ ff(xn)g, OTWE^A@]IH WSEWOZMOVNYM POSLEDOWATELXNOSTQM fxng TO- ^EK xn 6=a, SHODQ]IMSQ K TO^KE a.1 eSLI BY DLQ KAKOJ-TO POSLEDOWATELXNOSTI fx0ng OTLI^NYH OT a TO^EK, SHODQ]EJSQ K a, POSLEDOWATELXNOSTX ff(x0n)g SHODILASX K ^ISLU b0 6=b, TO DLQ POSLEDOWATELXNOSTI x1 x02 x3 x04 : : : (TAKVE SHODQ]EJ- SQ K a I SOSTOQ]EJ IZ TO^EK, OTLI^NYH OT a) POSLEDOWATELX-
NOSTX f(x1) f(x02) f(x3) f(x04) : : : , S ODNOJ STORONY (PO UVE DOKAZANNOMU), BYLA BY FUNDAMENTALXNOJ, A SLEDOWATELXNO,
SHODQ]EJSQ, TOGDA KAK, S DRUGOJ STORONY, IMEQ PODPOSLEDO-
WATELXNOSTI f(x1) f(x3) f(x5) : : : I f(x02) f(x04) f(x06) : : : ,
SHODQ]IESQ K RAZRYM PREDELAM, OKAZYWALASX BY RASHODQ-
]EJSQ | PROTIWORE^IE. Q.E.D.
wOT WAVNYJ DLQ PRILOVENIJ (W WOPROSAH SHODIMOSTI
NESOBSTWENNYH INTEGRALOW) WARIANT DOKAZANNOGO KRITERIQ DLQ ODNOSTORONNIH PREDELOW (NA PRIMERE LEWOSTORONNEGO).
1 w SILU KRITERIQ (\KWIWALENTNOGO OPREDELENIQ) PREDELA FUNKCII
\^EREZ POSLEDOWATELXNOSTI" \TO I BUDET OZNA^ATX, ^TO b =lim f (x).
x!a
136
fUNKCIQ y = f(x) (DEJSTWITELXNOJ PEREMENNOJ) IMEET W TO^KE a (WKL@^AQ SLU^AJ a = +1) PREDEL SLEWA TOGDA I TOLXKO TOGDA, KOGDA DLQ L@BOGO POLOVITELXNOGO ^ISLA
" SU]ESTWUET LEWAQ OKRESTNOSTX TO^KI a, W KOTOROJ ZNA- |
||||||||||||||||||
^ENIQ FUNKCII RAZNQTSQ MEVDU SOBOJ MENX[E, ^EM NA " |
||||||||||||||||||
FORMULXNO (SOOTWETSTWENNO SLU^AQM a |
2 R I a = +1): |
|
||||||||||||||||
9 |
b b = lim |
f(x) |
">0 |
9 |
>0 |
8 |
x0 |
8 |
x00 |
a |
<x0 |
< x00<a |
) |
|||||
; |
x!a;0 |
|
()8 |
|
|
|
; |
; |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
f(x0) |
; |
f(x00) |
<" , |
|||||
|
|
|
|
|
|
|
|
|
|
) j |
|
|
j |
|
|
|||
9 |
b b = lim f(x) |
">0 |
9 |
c>0 |
8 |
x0 |
8 |
x00 |
c<x0 < x00 |
) |
|
|||||||
; |
x!+1 |
|
()8 |
|
|
|
; |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
f(x0) |
; |
f(x00) |
<" . |
|||||
|
|
|
|
|
|
|
|
|
|
) j |
|
|
j |
|
|
|||
oGRANI^ENNOSTX I MONOTONNOSTX FUNKCIJ |
|
|
|
|||||||||||||||
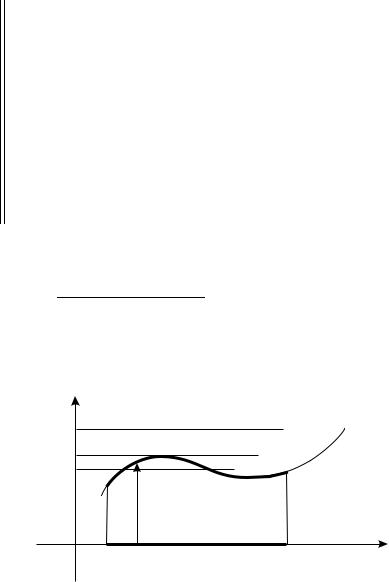
fUNKCI@ y = f(x) (S DEJSTWITELXNYMI ZNA^ENIQMI) NA-
ZYWA@T OGRANI^ENNOJ SWERHU NA MNOVESTWE X , ESLI ISTIN-
NO UTWERVDENIE |
9b8x x 2 X ) f(x) |
6 |
b |
, OZNA^A@]EE, ^TO |
|||||||
|
|||||||||||
OGRANI^ENO SWERHU MNOVESTWO |
def |
|
|
|
WSEH ZNA- |
||||||
YX = ff(x) j x 2 Xg |
|||||||||||
|
|
|
|
|
; |
|
|||||
^ENIJ, PRINIMAEMYH FUNKCIEJ NA MNOVESTWE X (RIS. 8). |
|||||||||||
|
|
|
b |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
y=f(x) |
|
|||
|
y |
|
|
|
|
|
|||||
x X
rIS. 8

137
zAMENA W POSLEDNEJ FORMULE NERAWENSTWA f(x) 6 b PROTI- WOPOLOVNO NAPRAWLENNYM f(x) > b PRIWODIT K OPREDELENI@ FUNKCII, OGRANI^ENNOJ SNIZU NA MNOVESTWE X.
gOWORQ OB OGRANI^ENNOSTI FUNKCII y = f(x) (PRINIMA- @]EJ DEJSTWITELXNYE ZNA^ENIQ NA MNOVESTWE X), PODRAZU-
MEWA@T EE OGRANI^ENNOSTX SWERHU I SNIZU |
, ^TO RAWNOSILXNO |
|||||||||||||||||||||||
ISTINNOSTI UTWERVDENIQ |
|
|
9c>08x |
; |
x 2 X ) jf(x)j 6 c |
|
.1 |
|
|
|
||||||||||||||
|
|
pRIMER |
. fUNKCIQ y = |
1 |
NA MNOVESTWE |
X = (0 + |
) OGRA- |
|||||||||||||||||
|
|
x |
||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
8 |
|
1 ) |
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
NI^ENA SNIZU, NO |
NE OGRANI^ENA SWERHU: |
|
x x > 0 |
|
10 < |
|
, |
|||||||||||||||||
|
|
x |
|
|||||||||||||||||||||
|
|
|
|
|
; |
|
|
|
; |
|
|
|
|
|
|
; |
|
|
|
|
|
|
||
|
8 |
|
9 |
|
^ x |
|
|
|
|
|
|
jbj+1 |
|
|
|
|
||||||||
NO |
|
|
b |
|
x x>0 |
|
|
> b DOSTATO^NO WZQTX x = |
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
eSLI FUNKCIQ y = f(x) OGRANI^ENA SWERHU NA MNOVESTWE
X , TO ^ISLO y = sup YX | TO^NU@ WERHN@@ GRANX MNOVES-
TWA ZNA^ENIJ \TOJ FUNKCII2 (SM. RIS. 8) | PRINIMA@T ZA
TO^NU@ WERHN@@ GRANX FUNKCII y = f(x) NA MNOVESTWE X
S OBOZNA^ENIEM |
|
= supf(x) FORMULXNO: |
|
= supf(x) |
def |
|||||||||||||||||
y |
y |
|||||||||||||||||||||
|
|
; |
|
|
|
X |
|
|
|
|
|
; |
|
|
|
|
X |
() |
|
|||
|
def |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2X ) f(x)6y |
|
^8">09x x2X |
^f(x) >y;" . |
||||||||||||||||
()8x x |
|
|||||||||||||||||||||
|
pODOBNYM OBRAZOM OPREDELQ@T |
TO^NU@ NIVN@@ GRANX |
|
|||||||||||||||||||
FUNKCII NA MNOVESTWE: y = inf f(x) |
|
def |
|
|
|
|
|
|||||||||||||||
|
def |
|
|
|
|
|
|
|
|
|
|
X |
() |
|
|
|
|
|
|
|
||
|
|
|
2X ) f(x)>y |
|
^8">09x x2X ^f(x)< y+" . |
|||||||||||||||||
()8x x |
|
|||||||||||||||||||||
|
eSLI VE; |
FUNKCIQ y = f(x) NE OGRANI^ENA; |
SWERHU NA MNO- |
|||||||||||||||||||
|
|
|
|
|
X |
1 |
|
|
|
; |
|
|
|
|
|
|||||||
VESTWE X, T. E. ISTINNO UTWERVDENIE |
8b9x |
x 2 X ^ f(x) >b , |
||||||||||||||||||||
TO POLAGA@T supf(x) = + |
|
|
|
SOOTWETSTWENNO, S^ITA@T, ^TO |
||||||||||||||||||
X |
|
|
;1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
inf f(x) = |
|
|
DLQ NE OGRANI^ENNOJ SNIZU FUNKCII. |
|
|
|||||||||||||||||
1 pOSLEDNQQ FORMULA RASPROSTRANQET PONQTIE OGRANI^ENNOSTI NA
KOMPLEKSNOZNA^NYE FUNKCII, DLQ KOTORYH PONQTIQ OGRANI^ENNOSTI SWERHU I OGRANI^ENNOSTI SNIZU LI[ENY SMYSLA.
2 sM. S. 42, TEOREMA O SU]ESTWOWANII TO^NYH GRANEJ.

138
fUNKCI@ y = f(x) DEJSTWITELXNOJ PEREMENNOJ NAZYWA@T
NEUBYWA@]EJ |
NA MNOVESTWE X |
R, |
ESLI ISTINNO UTWERV- |
|||||||||||||
DENIE |
8 |
x0 |
8 |
x00 x0 |
2 |
X |
^ |
x0 |
2 |
X |
^ |
x0 < x00 |
) |
f(x0) 6f(x00) ZAME- |
||
|
|
|
|
|
|
|
|
0 |
00 |
|||||||
NA W \TOJ FORMULE NERAWENSTWA f(x ) |
f(x ) NERAWENSTWAMI |
|||||||||||||||
6 |
OPREDE- |
f(x0) < f(x00) ;f(x0) >f(x00) f(x0) >f(x00) PRIWODIT K |
LENIQM SOOTWETSTWENNO WOZRASTA@]EJ, NEWOZRASTA@]EJ I UBYWA@]EJ FUNKCII NA MNOVESTWE X.
pERE^ISLENNYE WIDY FUNKCIJ OB_EDINQ@T OB]IM NAZWANIEM MONOTONNYE FUNKCII NA MNOVESTWE X, PRI \TOM WOZRASTA@]IE I UBYWA@]IE FUNKCII (A ONI QWLQ@TSQ ^ASTNYMI SLU^AQMI SOOTWETSTWENNO NEUBYWA@]IH I NEWOZRASTA@-
]IH)1 NAZYWA@T STROGO MONOTONNYMI.2
w DALXNEJ[EM MONOTONNYE FUNKCII BUDUT RASSMATRIWATXSQ ISKL@^ITELXNO NA PROMEVUTKAH | TEH MNOVESTWAH DEJSTWITELXNOJ OSI3, KOTORYE WMESTE S L@BYMI DWUMQ SWOIMI TO^KAMI SODERVAT I WSE PROMEVUTO^NYE MEVDU NIMI,
T. E. NA OTREZKAH, INTERWALAH, POLUINTERWALAH, LU^AH I NA WSEJ DEJSTWITELXNOJ OSI.
eSLI I | PROMEVUTOK, TO L@BAQ EGO TO^KA, OTLI^NAQ OT KONCEWOJ, QWLQETSQ WNUTRENNEJ TO^KOJ \TOGO PROMEVUTKA: ONA PRINADLEVAT EMU WMESTE S NEKOTOROJ OKRESTNOSTX@. pROMEVUTOK, W KOTORYJ NE WKL@^ENY EGO KONCEWYE TO^KI, NAZYWA@T OTKRYTYM (KAVDYJ TAKOJ PROMEVUTOK IMEET WID (a b), GDE ;16a<b 6+1).
1 tO, ^TO DOKAZANO DLQ NEUBYWA@]IH FUNKCIJ, SPRAWEDLIWO I DLQ
WOZRASTA@]IH (I TO VE W OTNO[ENII NEWOZRASTA@]IH I UBYWA@]IH
FUNKCIJ).
2 dLQ FUNKCIJ KOMPLEKSNOJ PEREMENNOJ I FUNKCIJ, PRINIMA@]IH KOMPLEKSNYE ZNA^ENIQ, PONQTIE MONOTONNOSTI LI[ENO SMYSLA.
eSLI W KA^ESTWE X WYSTUPAET MNOVESTWO N NATURALXNYH ^ISEL, TO DANNYE OPREDELENIQ MONOTONNYH FUNKCIJ PEREHODQT W PRIWEDENNYE NA S. 75 OPREDELENIQ MONOTONNYH POSLEDOWATELXNOSTEJ.
3 sODERVA]IH BOLEE ODNOJ TO^KI.

139
tEOREMA O PREDELAH NEUBYWA@]EJ FUNKCII. eSLI y = f(x) | NEUBYWA@]AQ FUNKCIQ NA PROMEVUTKE I R,
TO W TO^KAH c \TOGO PROMEVUTKA, OTLI^NYH OT EGO LEWOJ KONCEWOJ TO^KI, SU]ESTWUET PREDEL SLEWA f(c;0), A W TO^KAH
c PROMEVUTKA, OTLI^NYH OT EGO PRAWOJ KONCEWOJ TO^KI, |
PREDEL SPRAWA f(c+0), PRI \TOM f(c;0) 6f(c) 6f(c+0).1 dOKAZATELXSTWO2. pUSTX TO^KA c PROMEVUTKA I NE QWLQET-
SQ EGO LEWOJ KONCEWOJ TO^KOJ. mNOVESTWO ff(x) j x 2 I ^x<cg (ZNA^ENIJ FUNKCII W TO^KAH PROMEVUTKA I, LEVA]IH SLE-
WA OT TO^KI c), QWLQQSX NEPUSTYM I OGRANI^ENNYM SWERHU
(^ISLOM f(c)), IMEET TO^NU@ WERHN@@ GRANX. oBOZNA^IW EE
y (PRI \TOM y 6 f(c)), OSTAETSQ DOKAZATX, ^TO y = lim f(x).
x!c;0
tAK KAK y = sup(f(x) j x 2 I ^ x<cg, IZ OPREDELENIQ TO^- NOJ WERHNEJ GRANI MNOVESTWA (SM. S. 41) SLEDUET, ^TO:
A) f(x) 6 y DLQ WSEH x 2 I x<c
B) KAKIM BY NI BYLO POLOVITELXNOE ^ISLO ", W NEKOTOROJ FUNKCIQ PRINIMAET ZNA^ENIE f(x0) >y;". I ISPOLXZUQ NEUBYWANIE FUNKCII y = f(x) MOVNO PO\TOMU UTWERVDATX, ^TO DLQ WSEH
x 2 (c; c) WYPOLNQ@TSQ NERAWENSTWA y;"<f(x) 6y, IZ ^EGO SLEDUET, ^TO ^ISLO y (NE PREWOSHODQ]EE ^ISLA f(c)) QWLQETSQ DLQ FUNKCII y = f(x) PREDELOM SLEWA W TO^KE c. Q.E.D.
zAME^ANIE. pO \TOJ VE SHEME DOKAZYWAETSQ, ^TO ESLI LE- WAQ (SOOTWETSTWENNO, PRAWAQ) KONCEWAQ TO^KA PROMEVUTKA I NE WKL@^AETSQ W \TOT PROMEVUTOK, TO W NEJ SU]ESTWU- ET (WOZMOVNO, BESKONE^NYJ) PREDEL SPRAWA (SOOTWETSTWENNO,
SLEWA), SOWPADA@]IJ S inff(x) (SOOTWETSTWENNO, c supf(x)).
I I
1 tAKOE VE UTWERVDENIE | S ZAMENOJ POSLEDNIH NERAWENSTW NA PRO- TIWOPOLOVNO NAPRAWLENNYE | SPRAWEDLIWO DLQ L@BOJ NEWOZRASTA@- ]EJ FUNKCII NA PROMEVUTKE.
2 nAPRIMER, DLQ PREDELA SLEWA.

140
III.7. kAK PONIMA@T NEPRERYWNOSTX FUNKCII NA MNOVESTWE
fUNKCI@ y = f(x) NAZYWA@T NEPRERYWNOJ NA MNOVEST-
WE |
X,1 ESLI ISTINNO UTWERVDENIE, WYRAVAEMOE FORMULOJ |
|||||||||
|
|
|||||||||
|
e |
;e |
|
e |
e |
|
,2 |
|||
8x8">09 >08x |
x2X ^x2X ^jx;xj< )jf(x);f(x)j<" |
|||||||||
LIBO RAWNOSILXNOE EMU UTWERVDENIE: |
|
|
|
|
|
|||||
|
|
|
||||||||
|
\dLQ L@BOJ TO^KI x MNOVESTWA X I L@BOJ SHODQ]EJSQ |
|
|
|||||||
|
K NEJ POSLEDOWATELXNOSTI fxng TO^EK \TOGO MNOVESTWA |
|
|
|
|
|||||
|
|
|
|
eff(xn)g |
|
|
|
|
|
|
|
POSLEDOWATELXNOSTX |
ZNA^ENIJ FUNKCII W TO^KAH |
|
|
||||||
|
xn SHODITSQ K ZNA^ENI@ FUNKCII W TO^KE x". |
|
|
|
|
|
||||
|
|
wOT DOKAZATELXSTWO RAWNOSILXNOSTI \TIHeUTWERVDENIJ |
|
. |
||||||
|
|
|
||||||||
|
|
1. pUSTX DLQ FUNKCII y = f(x) I MNOVESTWA X PRIWE- |
||||||||
|
|
|
|
|
|
e |
||||
DENNAQ WY[E FORMULA IMEET ZNA^ENIE \ISTINA". |
eSLI x |
| |
||||||||
L@BAQ TO^KA MNOVESTWA X I fxng | L@BAQ SHODQ]AQSQ K |
||||||||||
NEJ POSLEDOWATELXNOSTX TO^EK MNOVESTWA X, TO, WZQW PROIZ-
WOLXNO POLOVITELXNOE ^ISLO " I SU]ESTWU@]EE DLQ NEGO
(SOGLASNO FORMULE) POLOVITELXNOE ^ISLO , MOVNO UTWERVDATX SU]ESTWOWANIE NATURALXNOGO ^ISLA n0 SO SWOJSTWOM:
ESLI n >n0, TO jxn |
; xj< , A SLEDOWATELXNO, (W SILU FORMU- |
||||
LY) jf(xn);f(x)j |
< ". |TIM DOKAZANA SHODIMOSTX POSLEDOWA- |
||||
|
ff(xn)g |
e |
f(x). |
|
|
TELXNOSTI |
|
|
K ZNA^ENI@ |
|
|
2. pUSTX DLQe |
FUNKCII y = f(x) I MNOVESTWA X WY[E- |
||||
PRIWEDENNAQ FORMULA IMEET ZNA^ENIEe |
\LOVX", T. E. ZNA^ENIE |
||||
\ISTINA" IMEET EE OTRICANIE
1 dEJSTWITELXNOJ OSI ILI KOMPLEKSNOJ PLOSKOSTI. mNOVESTWO X
PREDPOLAGAETSQ WHODQ]IM W MNOVESTWO OPREDELENIQ DANNOJ FUNKCII.
2~ITAETSQ: \kAKOWA BY NI BYLA TO^KA xe MNOVESTWA X , DLQ L@BOGO
POLOVITELXNOGO ^ISLA " SU]ESTWUET TAKOE POLOVITELXNOE ^ISLO ,
^TO DLQ L@BOJ TO^KI MNOVESTWA X, OTSTOQ]EJ OT TO^KI xe MENX[E, ^EM
, ( ) ( ) , ".
NA ZNA^ENIQ f x I f xe RAZLI^A@TSQ MENX[E ^EM NA "
