
Шведенко Начала математического анализа 2011
.pdf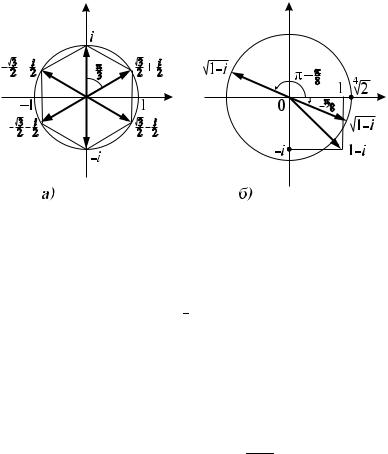
61
rIS. 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
sTOIT OTMETITX, ^TO IZ NAJDENNYH [ESTI ZNA^ENIJ p 1 |
|||||||||||||||||
; |
|
|
|
p3 |
|
i |
|
|
; |
|
|
|
p3 |
|
i |
|
; |
|
|
|
3 |
2 |
2 |
3 |
; |
|
|
2 |
|
2 |
|
|
|||||
^ISEL |
|
i |
|
|
|
|
TOLXKO TRI |
^ISLA |
|
i I |
|
|
+ |
|
|
SO- |
||
STAWLQ@T NABOR ZNA^ENIJ pi. oSTALXNYE TRI ^ISLA | \TO ZNA^ENIQ p;i.
iZWLEKATX KWADRATNYE KORNI IZ KOMPLEKSNYH ^ISEL MOVNO I NE PRIBEGAQ K IH POLQRNOJ ZAPISI, A NAPRQMU@ RE[AQ
DLQ DANNOGO KOMPLEKSNOGO ^ISLA a+ bi URAWNENIE z2 = a+ bi (ZAPISAW z = x+iy) KAK SISTEMU DWUH DEJSTWITELXNYH URAWNENIJ OTNOSITELXNO x I y.
|
nAPRIMER, ZADA^A NAHOVDENIQ 1 |
i = x+ iy PRIWODIT |
||||||||||||||||||||
K SISTEME |
x2 |
; |
y2 |
= 1 |
|
|
|
|
|
p ; |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
, RE[ENIE KOTOROJ DAET ZNA^ENIQ: |
|||||||||||||
|
|
|
(2xy = |
; |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
p |
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
||||
|
|
|
2+1 |
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1;i = q |
2 |
|
iq 2; |
|
. |
|
|
|
|
||||||||||||
p oPERIRUQ VE POLQRNOJ FORMOJ KOMPLEKSNOGO ^ISLA 1;i, |
||||||||||||||||||||||
MOVNO PRIJTI K TEM VE DWUM ZNA^ENIQM |
p |
1 |
; |
i , NO ZAPISAN- |
||||||||||||||||||
NYM W DRUGOM WIDE: |
|
|
|
|
|
|
|
|
|
|||||||||||||

62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1;i = p |
|
|
cos; |
|
+2k +i sin; |
|
|
|
+2k , |
|
|
|
||||||||||||||
2 |
|
|
|
|
|
|||||||||||||||||||||
4 |
4 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1;i = |
p |
|
+k +i sin; |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 cos; |
8 |
8 +k = |
|
|
|
||||||||||||||||||||
p |
|
|
; |
|
|
|
|
|
4 |
|
|
|
|
|
|
+ i sin( |
|
|
|
|||||||
|
|
|
|
|
= |
|
p2 cos |
; |
|
|
|
(RIS. 4, B). |
||||||||||||||
|
|
|
|
|
8 |
|
8 |
|||||||||||||||||||
iSPOLXZOWANIE EDINOGO SIMWOLA; |
|
|
|
|
|
1 |
|
|||||||||||||||||||
|
n |
|
n |
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
pa (ILI a ) DLQ OBOZNA- |
||||||||||||||||||||||||||
^ENIQ KAK WSEGO NABORA KORNEJ n-J STEPENI IZ ^ISLA a, TAK I KAVDOGO IZ NIH W OTDELXNOSTI, IMEET NEUDOBSTWA, SWQZANNYE, W ^ASTNOSTI, S TEM, ^TO W RAMKAH SISTEMY DEJSTWITELXNYH ^ISEL SIMWOLOM pn a PRINQTO OBOZNA^ATX ARIFMETI^ESKIJ
(EDINSTWENNYJ POLOVITELXNYJ) KORENX STEPENI n IZ POLO-
VITELXNOGO ^ISLA a. nAIBOLEE RAZUMNYJ WYHOD | WSQKIJ RAZ SPECIALXNO OGOWARIWATX, ^TO W KONKRETNOM SLU^AE POD- RAZUMEWAETSQ POD \TIM SIMWOLOM1.
k PRIMERU, OB]EIZWESTNAQ FORMULA KORNEJ KWADRATNOGO URAWNENIQ ax2 + bx + c = 0 DOPUSKAET DWE ZAPISI:
x = |
;b p |
|
|
I x = |
;b +p |
|
|
|
b2 |
;4ac |
b2 |
;4ac |
, |
||||
|
||||||||
|
2a |
|
|
2a |
|
|
||
PRI \TOM W RAMKAH SISTEMY DEJSTWITELXNYH ^ISEL PRIEM- LEMA LI[X ZAPISX SLEWA I TOLXKO PRI USLOWII b2 ;4ac > 0, A PRI DOPU]ENII MNIMYH KORNEJ PRIMENIMY OBE ZAPISI, ESLI S^ITATX, ^TO W ZAPISI SPRAWA RADIKAL IMEET DWA ZNA^ENIQ, A W ZAPISI SLEWA | KAKOE-LIBO ODNO IZ NIH.
1 oDIN IZ OSNOWOPOLOVNIKOW SOWREMENNOGO ANALIZA FRANCUZSKIJ MA-
TEMATIK kO[I (Cauchy Augustin-Louis, 1789{1857) W SWOEM ZNAMENITOM
\kURSE ANALIZA" [34] PREDLAGAL OBOJTI \TU TRUDNOSTX, ISPOLXZUQ ZA- PISX TIPA pa = pa, ODNAKO PODDERVKI W \TOM NE NA[EL.

63
II. Последовательности чисел
II.1. Что называют пределом числовой последовательности
Числовой последовательностью называют функцию натуральной1 переменной, принимающую числовые значения. Именно, говорят, что задана числовая последовательность2
{xn}, если каждому натуральному числу3 n сопоставлено некое число (действительное или мнимое), обозначаемое xn и называемое n-м элементом последовательности {xn}.
Вот фрагмент трактата 1800 г. французского математика Лакру´ (Lacroix Silvester Fran¸cois, 1765–1813): “Если, например, An = 3 + 2n, то беря последовательно n = 0, n = 1, n = 2, n = 3 и т. д., получили бы последовательность чисел 3, 5, 7, 9 и т. д.” 4
Имеются и такие варианты записи последовательности:
n →xn , n = 0, 1, 2, . . . ; {xn}+n=1∞; {xn}= xn1, xn1+1, . . . ;
постоянную последовательность c, c, . . . естественно обозначать {c} (не путая с одноэлементным множеством {c}).
Вместо xn в записи последовательности {xn} часто стоит указание вычислительных действий, которые надлежит совершить с числом n, чтобы получить n-й элемент после-
довательности. Например, у последовательности 1 1 n−
элемент x1 не определен, x2 = 1, x3 = 12 , . . . (или, если угодно, можно считать, что первый элемент последовательности отвечает значению n = 2, второй — значению n = 3 и т. д.).
1Вариант: целой неотрицательной.
2В дальнейшем для краткости просто последовательность.
3 |
Возможно, начиная с некоторого n = n1 (или, наоборот, с n = 0). |
4 |
В оригинале [43, с. 2] (в еще старой французской орфографии): |
“ Si l’on avoit, par exemple, An = 3+2n; en posant successivement n = 0, n =1, n =2, n =3, etc. on obtiendroit la suite des nombres 3, 5, 7, 9, etc.”

64
Число x называют пределом последовательности {xn}
(запись: lim xn = x)1, если истинно утверждение:
“ Для любого положительного числа, обозначаемого ε, существует такое натуральное число n0, что все элементы xn со значениями n > n0 попадают в ε-окрестность числа x, т. е. удовлетворяют неравенству |xn −x|< ε.”
Символически оно выражается формулой2
ε > 0 n0 n(n > n0 |xn −x|< ε) .
Из нее, в частности, следует, что если число ε > 0 брать сколь угод-
но малым, то натуральное число n0, для которого верно утверждениеn(n > n0 |xn−x|< ε), поневоле оказывается3 сколь угодно большим: если ε = |xm −x|, где xm — любой отличный от x элемент последова-
тельности {xn}, то неравенство |xn−x|< ε может выполняться для всех n > n0, лишь если n0 > m. Подчеркивая это обстоятельство, наряду с
lim xn =x часто пишут lim |
xn =x (а раньше писали lim xn =x). |
n→+∞ |
n=∞ |
Данное определение предела последовательности применимо к последовательностям {xn} как действительных ,
1 А также lim xn = x (особенно если существует зависимость xn
n→+∞
от других переменных, помимо n), {xn}→x и т. п.
2 На удобном для записи утверждений анализа “диалекте” языка
— языка логики первого порядка, предметными переменными в котором служат действительные числа. Все кванторы в этой формуле являются ограниченными: переменная ε принимает только положительные значения, а переменные n и n0 — только целые неотрицательные. Более подробную информацию касательно принципов
символической записи можно найти в Приложении I .
В случае последовательности {xn} действительных (но не комплексных) чисел эквивалентной формулой служит
µ ν(µ < x < ν n0 n(n > n0 µ < xn < ν))
(ее смысл: любой содержащий число x интервал содержит все элементы последовательности {xn} с достаточно большими “номерами”).
3 Если исключить нетипичный случай последовательности, все элементы которой, начиная с некоторого, равны числу x.

65
так и комплексных чисел (с записью их {zn} = {xn + iyn}). Различие лишь в геометрической трактовке неравенства |xn −x|< ε (а по сути ε-окрестности числа x). В “действительном” случае это неравенство означает, что элемент xn
попадает в интервал (x − ε, x + ε) действительной оси. В “комплексном“ же случае неравенство |zn −z|< ε выражает тот факт, что элемент zn = xn + iyn оказывается в круге радиуса ε с центром z = x+iy на комплексной плоскости, при этом lim zn = z в том и только в том случае, когда lim xn = x
и lim yn = y.
Последовательность, у которой есть предел, называют
сходящейся, а у которой нет предела — расходящейся. Символически сходимость последовательности {xn} вы-
ражается формулой
x ε > 0 n0 n(n > n0 |xn −x|< ε),
а ее расходимость — формулой, получаемой отрицанием :
x ε > 0 n0 n(n > n0 |xn −x| ε).
Примеры. 1. Постоянная последовательность {c}= c, c, . . .
является сходящейся (ее пределом служит число c).
2. Последовательность a (a — любое число) сходится, |
||||||
|
|
|
|
|
n |
|
и ее предел равен нулю. Доказать это — значит проверить |
||||||
истинность утверждения, выражаемого формулой |
||||||
|
ε > 0 |
|
n0 |
|
n n > n0 |
a < ε . |
|
|
|
n |
|||
Если для произвольно взятого положительного числа ε взять в качестве n0 любое натуральное число, превосходя-
щее число |a| (такое число n0 существует по аксиоме A9), то |
||
ε |
a |
< ε ” |
для натуральных чисел n утверждение “ n > n0 |
||
оказывается истинным 1. |
n |
|
1 Так же доказывается сходимость к нулю последовательностей
|
n |
√n |
|
√ε |
ε |
|||||
|
1 |
, |
1 |
(выбором соответственно n0 |
> |
1 |
и n0 > |
1 |
) и т. п. |
|
2 |
|
|
2 |
|||||||
|
|
|||||||||
66
3. Последовательность {(−1)n} является расходящейся. Доказывается это проверкой истинности утверждения
x ε > 0 n0 n(n > n0 |(−1)n −x| ε).
Каким бы ни было число x, взяв ε = 21 , можно утверждать, что для любого целого числа n0 хотя бы одно из неравенств |(−1)n0+1 − x| < ε или |(−1)n0+2 − x| < ε не выполняется: в противном случае оказывалось бы, что
2 = |(−1)n0+1 −(−1)n0+2| |(−1)n0+1−x|+|x−(−1)n0+2|< 2ε = 1.
Общие свойства сходящихся последовательностей
1. Сходящаяся последовательность имеет единственный предел.
Доказательство. Если предположить, что x = lim xn и x = lim xn (x =x), то каково бы ни было положительное число ε, для всех достаточно больших “номеров” n должны были бы выполняться неравенства |xn −x|< ε и |xn −x|< ε, из которых следовало бы, что
|x −x| = |(x −xn) + (xn −x)| |x −xn|+ |xn −x| < 2ε, что невозможно при выборе ε |x−2 x| .
2. Сходимость последовательности не нарушается (и величина ее предела сохраняется) при любом изменении в последовательности (равно как при удалении из нее или добавлении к ней) конечного числа начальных элементов.
Доказательство. Изменить в последовательности {xn} несколько начальных элементов — значит перейти к последовательности {xn} с xn = xn для всех n, начиная с некоторого n1. Удалить же из нее (соответственно, добавить к ней) начальный элемент — значит перейти к последовательности {xn+1} (соответственно последовательности {xn−1}).
Пусть последовательность {xn} сходится к числу x, т. е. истинно утверждение, выражаемое формулой

67
ε > 0 n0 n(n > n0 |xn −x|< ε).
Замена натурального числа n0, существующего (в силу данной формулы) для любого значения ε > 0, на наибольшее из чисел n0 и n1 позволяет сделать вывод об истинности утверждения, выражаемого формулой
ε > 0 n0 n(n > n0 |xn −x|< ε), —
о сходимости (к пределу x) последовательности {xn}. Подобным образом (заменой n0 , соответственно, на n0−1
и n0+1) выводится истинность утверждений о сходимости (к пределу x) последовательностей {xn+1} и {xn−1}.
3. Любая сходящаяся последовательность1 {xn} является ограниченной : все ее элементы не больше (по модулю)
некоторого положительного числа: h > 0 n(|xn| h).
Доказательство. Пусть ε — произвольно взятое положительное число. Тогда если x = lim xn , то для всех натуральных чисел n, б´ольших некоторого n0 , будет выполняться неравенство |xn −x| < ε, а следовательно, и неравенство
|xn|< |x|+ε. Пусть p — наибольшее из чисел |x1|, . . . , |xn0|, а h — наибольшее из чисел p и |x|+ε. Тогда |xn| h для всех
n, поскольку заведомо |xn| p при всех n n0 и |xn|< |x|+ε при всех n > n0 . Q.E.D.
Для последовательностей {xn} действительных чисел вводят также понятия ограниченности снизу a n(a xn) и ограниченности сверху b n(xn b) , при этом ограниченность последовательности {xn} равносильна ее ограниченности снизу и сверху.
В силу доказанного утверждения ограниченность последовательности есть необходимое условие ее сходимости. То, что это условие не является достаточным, видно на примере последовательности {(−1)n}.
1 Действительных или мнимых чисел.
68
4. Если последовательность {xn} сходится (к числу x) то последовательность {|xn|} также сходится (к числу |x|).
Доказательство. Формула
ε > 0 n0 n(n > n0 ||xn|−|x||< ε)
(выражающая то, что lim |xn| = |x|) есть следствие формулы
ε > 0 n0 n(n > n0 |xn −x|< ε)
и неравенства ||xn|−|x|| |xn −x|.
Арифметика сходящихся последовательностей
Среди сходящихся последовательностей особо выделяют те, которые сходятся к нулю, называя их бесконечно малы- ми. Их роль состоит, в частности, в том, что сходимость последовательности {xn} к числу x равносильна тому, что последовательность {xn −x} является бесконечно малой.
1)сумма (и разность) двух1 бесконечно малых последовательностей есть бесконечно малая последовательность;
2)произведение любой ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.
Доказательство. а) Пусть {αn} и {βn} — бесконечно малые последовательности (lim αn = lim βn = 0) и пусть ε — любое положительное число. Согласно определению предела последовательности для числа 2ε (как и для любого положительного числа) существуют такие натуральные числа n1 и n2 , что
|αn|< 2ε для всех n > n1 и |βn|< 2ε для всех n > n2.
Так как |αn ±βn| |αn|+ |βn|, выбором n0 = max{n1, n2}2 устанавливается истинность утверждения о том, что и по-
следовательности {αn ±βn} являются бесконечно малыми:
1А следовательно, и любого конечного числа.
2Т. е. n0 = n1, если n1 n2, и n0 = n2, если n1 < n2.

69
ε > 0 n0 n(n > n0 |αn ±βn|< ε).
б) Пусть {cn} — ограниченная последовательность (т. е. существует такое положительное число h, что |cn| h для всех элементов этой последовательности) и пусть последовательность {αn} является бесконечно малой. Каково бы ни было положительное число ε, можно утверждать (поскольку lim αn = 0), что для положительного числа hε существует такое натуральное число n0, что |αn| < hε для всех n > n0. Как следствие, |cnαn|= |cn||αn|< h hε = ε для всех n > n0, т. е. истинным оказывается утверждение:
ε > 0 n0 n(n > n0 |cnαn|< ε).
Если {xn} и {yn} — сходящиеся последовательности, то последовательности {xn ±yn} и {xn yn} также сходятся и
lim(xn±yn) = lim xn±lim yn , а lim(xn yn) = (lim xn)(lim yn);
если к тому же lim yn =,0то сходящейся является и по-
следовательность xn , причем lim yn
Доказательство. Если последовательности {xn} и {yn} сходятся, имея пределами числа x и y , то последовательности {xn−x} и {yn−y} являются бесконечно малыми. В соответствии с установленными свойствами бесконечно малых последовательностей1 бесконечно малыми являются также последовательности
{(xn ±yn)−(x±y)} = {(xn −x)±(yn −y)}
и
{xn yn −xy} = {xn(yn −y)+(xn −x)y},
а следовательно, последовательности {xn±yn} и {xn yn} сходятся, причем
lim(xn ±yn) = lim xn ± lim yn и lim(xn yn) = (lim xn)(lim yn).
1С учетом ограниченности сходящихся последовательностей {xn}
и{y} (постоянной последовательности).
70
Если lim yn = y =,0то для положительного числа |y2|
существует натуральное число n1 со свойством: |yn−y|< |y2| для всех натуральных чисел (“номеров”) n > n1 ; как след-
ствие, при n > n1 имеет место неравенство |yn| > |y2| , в силу которого определена и оказывается ограниченной последова-
тельность 1 +∞ . Остается заметить, используя запись
yn n=n1+1
xn |
x = xn |
|
x |
+ |
x |
x |
= |
|
1 |
(xn |
|
x) |
|
x |
1 |
1 |
(yn |
|
y) |
− yn |
|
|
− |
− |
|
− |
|||||||||||||
yn |
− y yn |
yn − y |
|
{yn |
|
|
y yn |
} |
|||||||||||
и свойства бесконечно малых последовательностей, что по-
следовательность xn − x является бесконечно малой, а по- yn y
этому lim xn = x . yn y
Сходимость и неравенства, “принцип сэндвича”
Если сходящиеся последовательности1 {xn} и {yn} таковы, что xn yn для всех натуральных чисел (“номеров”) n,
начиная с некоторого, то lim xn lim yn .
Доказательство. Пусть lim xn = x и lim yn = y. Рассуждая “от противного”, т. е. предполагая, что x > y, приходится
делать вывод: для положительного числа |
x−y существуют |
|||||||||||||||||||||||
такие натуральные числа n1 и n2, что |
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
| |
x |
n − |
x |
< |
x−y |
, |
т. е. |
x |
− |
x−y |
< x |
n |
< x+ |
x−y |
|
для всех |
n > n |
1, |
||||||
|
|
| |
2 |
|
|
2 |
|
|
2 |
|
|
|
||||||||||||
а |
|
|
|
|
|
|
x−y |
, |
т. е. |
|
|
|
x−y |
|
|
|
|
x−y |
|
для всех |
|
2, |
||
| |
y |
|
y |
< |
y |
− |
|
< y |
n |
< y + |
|
n > n |
||||||||||||
|
|
n− | |
2 |
|
2 |
|
|
2 |
|
|
||||||||||||||
и, как следствие, |
yn < |
x+y |
< xn |
для любого n, превосхо- |
||||||||||||||||||||
2 |
||||||||||||||||||||||||
дящего оба числа n1, n2, а это несовместимо с тем, что по |
||||||||||||||||||||||||
условию xn yn |
для всех натуральных чисел n, начиная |
|||||||||||||||||||||||
с некоторого. Пролученное противоречие доказывает, что неравенство lim xn > lim yn неверно.
1 Действительных чисел.
