
Шведенко Начала математического анализа 2011
.pdf
184
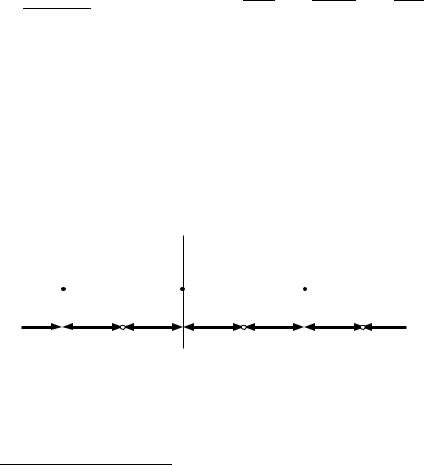
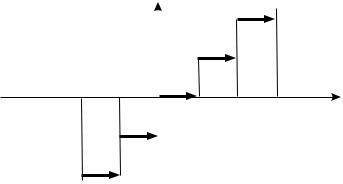
7. dLQ FUNKCII y = [x] (CELAQ ^ASTX ^ISLA x RIS. 13) KAVDOE CELOE ZNA^ENIE x QWLQETSQ TO^KOJ LEWOSTORONNEGO RAZRYWA 1-GO RODA (SO SKA^KOM 1).
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
0 |
|
|
1 |
|
|
2 |
|
|
|
|
3 |
x |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
rIS. 13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
ESLI x = 0 |
|
|
|
|
||||||||
8. fUNKCIQ y = |
lim |
|
px |
= |
|
IMEET PRI |
|||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
(1 ESLI x > 0 |
|
|
|
|
||||||||||
|
|
|
|
n!+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x = 0 PRAWOSTORONNIJ RAZRYW 1-GO RODA (SO SKA^KOM 1). |
|||||||||||||||||||||||||||||
9. fUNKCIQ y = ln x NE IMEET TO^EK RAZRYWA, TOGDA KAK |
|||||||||||||||||||||||||||||
|
! 1 |
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
( |
0 |
|
ESLI x = 0 |
|
|
|
|||||||
FUNKCIQ y = lim n |
|
px |
; |
|
|
|
px |
|
= |
|
|
ln x |
ESLI x > 0 |
IMEET |
|||||||||||||||
n |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
PRI x = 0 PRAWOSTORONNIJ RAZRYW 2-GO RODA. |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
sin |
1 |
|
|
|
|
|
sin |
1 |
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
10. dLQ FUNKCIJ y = |
|
|
|
|
1 |
|
I y = |
|
1 |
|
|
ZNA^ENIQ x = k , |
|||||||||||||||||
|
|
|
|
|
|
sin |
|
|
|
|
|
|
j sin |
|
j |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||
k = 1 2 : : : , QWLQ@TSQ TO^KAMI RAZRYWA: USTRANIMOGO |
|||||||||||||||||||||||||||||
DLQ PERWOJ FUNKCII I 1-GO RODA DLQ WTOROJ. |
zNA^ENIE VE |
||||||||||||||||||||||||||||
x = 0 WYHODIT ZA RAMKI DANNOGO WY[E OPREDELENIQ TO^KI RAZRYWA, ODNAKO, NAIBOLEE RAZUMNO, PO-WIDIMOMU, S^ITATX x = 0 TO^KOJ USTRANIMOGO RAZRYWA DLQ PERWOJ FUNKCII I TO^KOJ RAZRYWA 2-GO RODA DLQ WTOROJ.

185
IV. pROIZWODNAQ I DIFFERENCIAL FUNKCII
IV.1. ~TO NAZYWA@T PROIZWODNOJ FUNKCII I EE DIFFERENCIALOM
dIFFERENCIALXNOE IS^ISLENIE WOZNIKLO W KONCE XVII W.
W RABOTAH nX@TONA I lEJBNICA1 KAK METOD IZU^ENIQ FUNK- CIJ PUTEM SRAWNENIQ \BESKONE^NO UMALQ@]IHSQ" RAZNOSTEJ
x ;x0 |
I y ;y0 = f(x) ;f(x0) | ZNA^ENIJ PEREMENNOJ x I EE |
|||||||||||||||||||
FUNKCII y |
= f(x). |TI RAZNOSTI STALI OBOZNA^ATX Mx I |
|||||||||||||||||||
M y |
|
(ILI Mf ) I NAZYWATX |
PRIRA]ENIQMI |
PEREMENNOJ x I |
||||||||||||||||
FUNKCII y = f(x) \TOJ PEREMENNOJ W TO^KE x0 . |
|
|
||||||||||||||||||
|
pRIRA]ENIE My = f(x);f(x0) = f(x0 +Mx);f(x0) (FUNKCII |
|||||||||||||||||||
y = f(x) W TO^KE x0) QWLQETSQ PRI \TOM FUNKCIEJ PRIRA]E- |
||||||||||||||||||||
NIQ Mx (PEREMENNOJ x W TO^KE x0 ), A DOPUSTIMYMI ZNA^E- |
||||||||||||||||||||
NIQMI PRIRA]ENIQ |
x QWLQ@TSQ WSE TE (NENULEWYE) ^ISLA, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
DLQ KOTORYH ZNA^ENIE f(x0+ Mx) OPREDELENO2. |
|
|
|
|||||||||||||||||
|
pRIMER |
. eSLI y = x2, A x0 | L@BAQ TO^KA DEJSTWITELXNOJ |
||||||||||||||||||
|
|
|||||||||||||||||||
OSI, |
TO DOPUSTIMYM ZNA^ENIEM |
x QWLQETSQ L@BOE |
(NENULE- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
WOE |
) |
^ISLO |
, |
A My |
= |
x2 |
; |
x 2 |
|
x |
Mx |
2 |
; |
x 2 |
x |
Mx |
Mx 2 |
|||
|
|
|
|
|
0 |
= ( 0 |
+ ) |
|
0 = 2 |
0 |
|
+ ( ) . |
||||||||
|
oSNOWNYE PONQTIQ DIFFERENCIALXNOGO IS^ISLENIQ | \TO |
|||||||||||||||||||
DIFFERENCIAL FUNKCII I EE PROIZWODNAQ. |
|
|
|
|||||||||||||||||
|
pERWOE WNQTNOE (I DEJSTWU@]EE PO SEJ DENX) OPREDELENIE |
|||||||||||||||||||
DIFFERENCIALA FUNKCII DAL PORTUGALXSKIJ MATEMATIK DA |
||||||||||||||||||||
kUNXQ |
3 (NAZYWAW[IJ DIFFERENCIAL \FL@KSIEJ"4). |
|
||||||||||||||||||
1 wYDERVKI IZ \TIH RABOT (W RUSSKOM PEREWODE) MOVNO NAJTI W HRES-
TOMATII [30] (S. 95{116). tERMIN DIFFERENCIALXNOE IS^ISLENIE WWEL lEJBNIC (LAT. di erentia | RAZLI^IE, RAZNOSTX).
2 w ^ASTNOSTI, ESLI FUNKCIQ OPREDELENA W -OKRESTNOSTI TO^KI x0 ,
TO DOPUSTIMYMI DLQ Mx BUDUT WSE (NENULEWYE) ZNA^ENIQ S |
j |
Mx |
< . |
3 Da Cunha Joseph-Anastase, 1744{1787. |
j |
|
4 lAT. uxio TE^ENIE. nX@TON (W OTLI^IE OT DA kUNXI) NAZYWAL
FL@KSIEJ TO, ^TO SEJ^AS NAZYWA@T PROIZWODNOJ.

186
dIFFERENCIALOM FUNKCII y = f(x) (W TO^KE x0) NAZYWA- @T OBOZNA^AEMU@ dy (ILI df ) I ZAWISQ]U@ OT PRIRA]ENIQ
Mx = x;x0 WELI^INU, KOTORAQ:
A) PROPORCIONALXNA Mx (T. E. IMEET WID dy = a Mx)
B) OTLI^AETSQ OT PRIRA]ENIQ FUNKCII My (WYZWANNOGO
PRIRA]ENIEM Mx PEREMENNOJ x) NA BESKONE^NO MALU@ OTNO-
SITELXNO Mx, T. E. My ;dy = o(Mx) PRI Mx!0.1
fUNKCI@, U KOTOROJ SU]ESTWUET DIFFERENCIAL W TO^KE x0, NAZYWA@T DIFFERENCIRUEMOJ W \TOJ TO^KE.
nAPRIMER, PRIRA]ENIE FUNKCII y = x3 W KAKOJ-LIBO TO^-
KE x0 ESTX My = (x0 +Mx)3 ; x03 = 3x02Mx + 3x0(Mx)2 +(Mx)3, IZ ^EGO SLEDUET, ^TO DANNAQ FUNKCIQ DIFFERENCIRUEMA W L@-
BOJ TO^KE x0 , IMEQ W NEJ DIFFERENCIAL dy = 3x02Mx. pROIZWODNOJ FUNKCII y = f(x) (W TO^KE x0) NAZYWA@T
^ISLO f0 x |
def |
My |
= lim |
f(x0 |
+Mx) ;f(x0) |
( |
PRI USLOWII |
, |
^TO |
( |
0) = lim |
|
|
Mx |
|
|
|||
|
Mx!0 Mx |
Mx!0 |
|
|
|
|
|
||
\TOT PREDEL SU]ESTWUET.2 |
|
|
|
|
|
|
|||
1 dOSLOWNO (NA S. 197 FRANCUZSKOGO IZDANIQ UDIWITELXNOGO PO ^ET- KOSTI I KRATKOSTI IZLOVENIQ U^EBNIKA DA kUNXI [37]): \ ... on designe de m^eme par d;x, et on appelle uxion de ;x, la grandeur qui rendroit
|
d;x |
|
|
;(x+dx) |
;x |
|
d;x |
|
|
|
||
|
dx |
constante, et |
|
|
dx ; |
|
; |
dx |
in nitieme ou zero, si dx devenoit |
|||
in nitieme, et si tout ce qui ne depend pas de dx demeroit constant". |
||||||||||||
|
2 nARAWNE S |
|
( |
0) |
|
|
( 0). |
|
( |
|
||
|
f0 x |
|
PI[UT |
y0 |
x |
tERMIN PROIZWODNAQ |
|
fonction |
||||
derivee) I [TRIH (ZNAK PRIM) KAK SIMWOL WZQTIQ PROIZWODNOJ WWEL FRANCUZSKIJ MATEMATIK lAGRANV (Lagrange, Joseph Louis, 1736{1813)
PROIZWODNU@ ON OPREDELQL (NA S. 14 W [44]) ^ISTO ALGEBRAI^ESKI, NE PRI- BEGAQ K PREDELU, O ^EM I GOWORIT POLNOE NAZWANIE EGO MONOGRAFII [44]: \tEORIQ ANALITI^ESKIH FUNKCIJ, SODERVA]AQ PRINCIPY DIFFERENCI- ALXNOGO IS^ISLENIQ, O^I]ENNYE OT KAKOGO BY TO NI BYLO RASSMOTRE- NIQ BESKONE^NO MALYH ILI IS^EZA@]IH, PREDELOW ILI FL@KSIJ I SWE- DENNYE K ALGEBRAI^ESKOMU ANALIZU KONE^NYH WELI^IN" (\Theorie des fonctions analytiques contenant les principes du calcul di erentiel, degages de toute consideration d'in niment petits ou d'evanouissans, de limites ou de uxions et reduits a l'analyse algebrique des quantites nies").

187
fUNKCIQ y = f(x) QWLQETSQ DIFFERENCIRUEMOJ W TO^KE x0 TOGDA I TOLXKO TOGDA, KOGDA ONA IMEET W \TOJ TO^KE PROIZ-
WODNU@, PRI \TOM PROIZWODNAQ I DIFFERENCIAL FUNKCII
(W TO^KE x0) SWQZANY SOOTNO[ENIEM df = f0(x0)Mx. dOKAZATELXSTWO. sU]ESTWOWANIE W TO^KE x0 PROIZWODNOJ
OZNA^AET, ^TO MMfx ;f0(x0) = o(1) PRI Mx !0,1
ILI, ^TO TO VE SAMOE, Mf ; f0(x0) Mx = o(Mx) PRI Mx!0, A \TO I OZNA^AET SU]ESTWOWANIE U FUNKCII y = f(x) DIFFE-
RENCIALA df = f0(x0)Mx W TO^KE x0. Q.E.D.
zAME^ANIE. wWIDU DOKAZANNOJ RAWNOSILXNOSTI TREBOWA-
NIJ DIFFERENCIRUEMOSTI I SU]ESTWOWANIQ PROIZWODNOJ IH NEREDKO SME[IWA@T, NAZYWAQ FUNKCI@ DIFFERENCIRUEMOJ, ESLI ONA IMEET PROIZWODNU@. |TOGO NE STOIT DELATX HOTQ BY POTOMU ^TO PRI PEREHODE K FUNKCIQM NESKOLXKIH PEREMEN- NYH UKAZANNYE TREBOWANIQ STANOWQTSQ NERAWNOSILXNYMI:
sLEDU@]EE UTWERVDENIE ^ASTO NAZYWA@T NEOBHODIMYM USLOWIEM DIFFERENCIRUEMOSTI FUNKCII:
eSLI FUNKCIQ DIFFERENCIRUEMA2 W TO^KE, TO ONA NEPRE- RYWNA W \TOJ TO^KE.
dOKAZATELXSTWO. pEREHODOM K PRIRA]ENIQM Mx = x ;x0
I Mf = f(x) ; f(x0) USLOWIE lim f(x) = f(x0) NEPRERYWNOS-
x!x0
TI FUNKCII W TO^KE x0 PREOBRAZUETSQ K WIDU lim Mf = 0.
Mx!0
~TOBY DOKAZATX WYPOLNENIE POSLEDNEGO SOOTNO[ENIQ W SLU-
^AE DIFFERENCIRUEMOSTI (A SLEDOWATELXNO SU]ESTWOWANIQ
PROIZWODNOJ) FUNKCII y = f(x) W TO^KE x0 |
DOSTATO^NO ZAPI- |
|||||||||||
SATX: lim |
Mf = lim |
Mf |
Mx = f0(x0) |
|
0 = 0. Q.E.D. |
|||||||
Mx!0 |
Mx!0 Mx |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Mf |
|
|
|
|
||
1 t. E. RAZNOSTX MEVDU OTNO[ENIEM |
|
0 |
(x0) ESTX BESKO- |
|||||||||
Mx |
I ^ISLOM f |
|||||||||||
2 |
|
! |
0. |
|
|
|
|
|
|
|
|
|
NE^NO MALAQ PRI Mx |
|
|
|
|
|
|
|
|
|
|
||
iLI, ^TO \KWIWALENTNO, IMEET PROIZWODNU@.

188
tO, ^TO NEPRERYWNOSTX QWLQETSQ LI[X NEOBHODIMYM (NO
NE DOSTATO^NYM) USLOWIEM DIFFERENCIRUEMOSTI FUNKCII,
WIDNO IZ SLEDU@]IH DWUH PRIMEROW. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1. y = jx |
;x0j. pRIRA]ENI@ Mx = x ;x0 |
SOOTWETSTWUET |
||||||||||||||||||||||||||||
PRIRA]ENIE |
My = jx;x0j, IZ ^EGO SLEDUET: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
A) |
lim Mf = lim |
|
Mx |
j |
= 0, A POTOMU FUNKCIQ y = |
j |
x |
; |
x0 |
j |
||||||||||||||||||||
|
Mx!0 |
|
|
|
Mx!0j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
QWLQETSQ NEPRERYWNOJ W TO^KE x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
B) U FUNKCII y = jx;x0j NET PROIZWODNOJ W TO^KE x0 : OT- |
||||||||||||||||||||||||||||||
NO[ENIE My |
= jx;x0j |
NE IMEET PREDELA W TO^KE x0 , POSKOLXKU |
|||||||||||||||||||||||||||||
|
|
Mx x;x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
lim |
jx;x0j = |
|
1, A |
lim |
jx;x0j = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x!x0;0 |
x;x0 |
|
; |
|
|
x!x0+0 |
x;x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
zAME^ANIE |
. w PODOBNYH SLU^AQH (KOGDA OTNO[ENIE MMxy , |
|||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
NE IMEQ PREDELA PRI x |
! |
0, IMEET PREDEL PRI x |
! |
0 |
; 0 |
||||||||||||||||||||||||||
I/ILI x ! |
0 + 0) GOWORQT, ^TO FUNKCIQ y = f(x), |
NE IMEQ |
|||||||||||||||||||||||||||||
PROIZWODNOJ W TO^KE x0, IMEET W \TOJ TO^KE LEWU@ I/ILI |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
def |
|
|
|
My |
I y |
0 |
|
def |
|
|
|
|
|
My |
. |
||
PRAWU@ PROIZWODNYE y;(x0) = lim |
|
M |
+ |
(x0) = lim |
|
M |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
0 |
|
|
|
x |
|
|
0+0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
x |
|
|
|
|
! |
|
x |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
! |
|
|
|
|
|
M |
|
|
|
|
||||||
|
|
( |
x sin |
1 |
, |
ESLI x 6= 0 pRIRA]ENIQMI PEREMENNYH |
|||||||||||||||||||||||||
|
2. y = |
x |
|||||||||||||||||||||||||||||
|
|
|
|
0 |
|
ESLI x = 0: |
|
|
|
|
|
|
|
|
|
|
|
x = x I |
|||||||||||||
x I y W TO^KE |
x = 0 W DANNOM SLU^AE QWLQ@TSQ |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
||
My = x sin x1 , IZ ^EGO SLEDUET:
|
|
A) lim |
M |
|
limx |
|
sin |
1 |
|
1 |
T. E. DANNAQ FUNKCIQ NEPRE- |
|||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
y = |
|
x |
= 0, |
|||||||||||||||||
|
|
Mx!0 |
|
|
x!0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
RYWNA W TO^KE 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0 |
|
def |
|
My |
|
|
1 |
|
NE OPREDELENO.2 |
|
||||||
|
|
B) ZNA^ENIE y |
|
(0) = lim |
|
= |
lim sin |
|
|
|||||||||||||
|
|
|
|
x |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Mx!0 Mx |
|
x!0 |
|
|
|
|
|
|||||
|
|
|
|
|
||||||||||||||||||
|
|
1 kAK PROIZWEDENIE BESKONE^NO MALOJ (PRI x |
0) NA OGRANI^ENNU@. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! 0 |
def |
My |
I |
|
|
|
2 nE OPREDELENY W DANNOM SLU^AE I ZNA^ENIQ y;(0) = |
lim |
|
||||||||||||||||||
|
|
|
|
My |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mx!0;0 Mx |
|
|
y |
0 |
def |
|
| LEWAQ I PRAWAQ PROIZWODNYE FUNKCII PRI x = 0. |
||||||||||||||||||
+ |
(0) = lim |
|
||||||||||||||||||||
|
Mx!0+0 Mx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

189
pROIZWODNYE KOMBINACIJ FUNKCIJ
|
|
eSLI OBE FUNKCII y = f(x) I y = g(x) IME@T PROIZWODNYE |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
(SOOTWETSTWENNO f 0(x0) I g0(x0)) W TO^KE x0, TO W \TOJ TO^KE |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
IME@T PROIZWODNYE TAKVE SUMMA, RAZNOSTX I PROIZWEDE- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
0) 6= 0 |
|
|
|
|
|
|
|
, |
||||||
|
|
NIE \TIH FUNKCIJ |
|
|
|
A PRI USLOWII |
g x |
|
|
|
|
|
I IH |
|
^ASTNOE |
|
|||||||||||||||||||||||||||||||||
|
|
PRI \TOM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
(f |
g)0(x0) = f 0(x0) |
|
g0(x0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
(f g)0(x0) = f 0(x0)g(x0) +f(x0)g0(x0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
f |
|
0 |
x |
|
f 0 |
x |
|
g x |
|
|
|
|
f x |
0) |
g0 x |
0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
; |
|
|
|
( 0) |
( 0); ( |
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
g |
|
( 0) = |
|
|
|
|
|
|
|
|
2 |
( |
|
0) |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
dOKAZATELXSTWO |
. eSLI Mx = x;x0 , TO |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
W SILU ^EGO |
Mf = f(x) ;f(x0) Mg = g(x) ;g(x0), |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
;f(x) g(x) ;;f(x0) g(x0) =Mf Mg, |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
M(f g) = |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
M(f g) = f(x) g(x);f(x0) g(x0) = |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
= |
f(x0)+Mf |
|
|
|
g(x0)+Mg |
; |
f |
(x0) g(x0) = |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
( |
|
|
|
0) + |
|
( 0) |
|
|
|
|
|
+ |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
M f = |
|
|
Mf g x |
|
|
|
|
|
f x |
|
|
Mg |
|
Mf Mg |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
( ) |
|
( |
|
0) |
|
|
= |
|
( |
|
( |
0)+ ) |
|
( 0);( ( 0)+ |
) ( |
|
0) |
|
= |
|
|
|
|||||||||||||||||||||||||
; |
|
|
|
f x |
|
|
f x |
|
|
|
|
|
|
|
|
f x |
Mf |
g x |
|
g x |
|
|
0) |
Mg f x |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
( ) ; |
( |
0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
( ( 0)+ |
) ( |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
g |
|
|
|
g x |
|
|
g x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g x |
|
Mg g x |
|
|
( 0); |
|
|
( |
0) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mf g x |
|
|
f x |
Mg |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
( 0)+ |
|
|
|
) |
( 0) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g x |
Mg |
g x |
|
|
||||
POSLEDU@]IM DELENIEM NA Mx I USTREMLENIEM EGO K NUL@1 USTANAWLIWAETSQ SU]ESTWOWANIE
lim M(f g) = f 0(x0) g0(x0),
Mx!0 Mx
lim M(fxg) = f 0(x0)g(x0) +f(x0)g0(x0),
Mx!0 M
1 pRI \TOM Mf I Mg TAKVE STREMQTSQ K NUL@.

190
|
f |
|
|
|
|
lim |
M;g |
= f 0(x0)g(x0)2 |
;f(x0)g 0(x0) |
. Q.E.D.1 |
|
Mx |
|||||
Mx!0 |
g |
(x0) |
|
tEOREMA O PROIZWODNOJ SLOVNOJ FUNKCII. eSLI FUNKCIQ x = '(t) IMEET W TO^KE t0 PROIZWODNU@ '0(t0), A
FUNKCIQ y = f(x) IMEET W TO^KE |
x0 = '(t0) PROIZWODNU@ |
||||
f 0(x0), TO KOMPOZICIQ |
; |
\TIH FUNKCIJ2 IMEET W |
|||
y = f '(t) |
|||||
TO^KE t0 PROIZWODNU@ |
y0(t0) = f 0(x0)'0(t0) |
.3 |
|||
|
dOKAZATELXSTWO |
. pUSTX Mt = t |
; t0 | L@BOE, NO DOSTA- |
||
|
|
||||
TO^NO MALOE PO ABSOL@TNOJ WELI^INE PRIRA]ENIE PEREMEN- |
|||||
NOJ t W TO^KE t0 .4 sOOTWETSTWU@]EE \TOMU PRIRA]ENI@ Mt PRIRA]ENIE Mx = x ;x0 = '(t) ;'(t0) PREDSTAWIMO (WWIDU DIFFERENCIRUEMOSTI FUNKCII x = '(t) W TO^KE t0 ) W FORME
Mx = '0(t0)Mt + o(Mt) Mt!0
W SWO@ O^EREDX OTWE^A@]EE \TOMU PRIRA]ENI@ Mx PRIRA-
]ENIE My = f(t) ;f(t0) PREDSTAWIMO (WWIDU DIFFERENCIRUE-
MOSTI FUNKCII y = f(x) W TO^KE x0) W FORME
My = f 0(x0)Mx + o(Mx) Mx!0.
pODSTANOWKA W PRAWU@ ^ASTX POSLEDNEGO RAWENSTWA WMESTO Mx EGO PREDSTAWLENIQ Mx = '0(t0)Mt+o(Mt) S U^ETOM TOGO,
1 tAK KAK PROIZWODNAQ POSTOQNNOJ FUNKCII RAWNA NUL@, SLEDSTWI- EM DOKAZANNOGO UTWERVDENIQ QWLQETSQ FORMULA PROIZWODNOJ LINEJNOJ
|
|
|
|
|
|
|
|
|
|
: |
( |
+ |
|
) ( |
0) = |
|
|
( 0)+ |
|
|
( 0) |
, |
|
|
|
| |
||
KOMBINACII FUNKCIJ |
|
|
f |
|
g 0 x |
|
f0 |
x |
|
|
|
g0 x |
|
GDE |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
L@BYE (DEJSTWITELXNYE ILI MNIMYE) ^ISLA. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
2 iLI, KAK E]E GOWORQT, SLOVNAQ FUNKCIQ. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
3 |
fORMULA PROIZWODNOJ SLOVNOJ FUNKCII |
, ILI \ |
CEPNOE PRAWILO |
". |
|||||||||||||||||||||||
|
4 oNO BUDET DOPUSTIMYM KAK DLQ FUNKCII |
x = '(t), TAK I DLQ |
||||||||||||||||||||||||||
FUNKCII y = f '(t) : ESLI ZNA^ENIE |
j Mtj |
DOSTATO^NO MALO, TO TO^KA |
||||||||||||||||||||||||||
|
= |
|
0 + |
|
|
|
|
; |
|
|
|
|
|
|
|
|
0 , |
|
|
|
|
|
|
|
|
|
||
t |
|
t |
|
|
Mt POPADAET W TU OKRESTNOSTX TO^KI t |
W KOTOROJ OPREDELENA |
||||||||||||||||||||||
FUNKCIQ x = '(t), TAK VE KAK (POSKOLXKU Mt ! 0 |
=) Mx ! 0) ZNA^ENIE |
|||||||||||||||||||||||||||
|
( ) = |
|
|
= |
|
0+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
, |
|
|
|
||
' t |
|
|
x |
|
x |
|
Mx OKAZYWAETSQ W TOJ OKRESTNOSTI TO^KI x |
|
|
W KOTOROJ |
||||||||||||||||||
OPREDELENA FUNKCIQ y = f(x).

 y
y y
y