Шведенко Начала математического анализа 2011

111

2. pUSTX UTWERVDENIE A) LOVNO, T. E. ISTINNO EGO OTRI-

CANIE

9">0 8 >0 9x;jx;aj< ^;jf(x);f(a)j>" _ :!f(x) _ :!f(a) . pOSLEDOWATELXNO POLAGAQ W \TOJ FORMULE = 1 12 13 : : :

I OBOZNA^AQ x1 x2 x3 : : : ZNA^ENIQ x, SU]ESTWU@]IE DLQ \TIH ZNA^ENIJ , POLU^A@T POSLEDOWATELXNOSTX fxng TO^EK

xn, DLQ KOTOROJ ODNOWREMENNO jxn;aj< n1 I jf(xn);f(a)j>" (LIBO ZNA^ENIQ f(xn) I/ILI f(a) NE OPREDELENY). pOSTROEN- NAQ POSLEDOWATELXNOSTX fxng OBLADAET PO\TOMU SWOJSTWOM: ONA SHODITSQ K TO^KE a, ODNAKO NE WERNO, ^TO POSLEDOWA- TELXNOSTX ff(xn)g ZNA^ENIJ FUNKCII W TO^KAH xn SHODITSQ K ZNA^ENI@ f(a). Q.E.D.

w ROSSIJSKOJ (A TO^NEE, MOSKOWSKOJ) PRAKTIKE PREPODAWANIQ MA- TEMATI^ESKOGO ANALIZA RASPROSTRANENA (NO NE WSEMI PODDERVIWAETSQ) TERMINOLOGIQ, SOGLASNO KOTOROJ W WY[EPRIWEDENNYH KRITERIQH (SM. S. 109, 110) FORMULXNYE ZAPISI UTWERVDENIJ A) QWLQ@TSQ OPREDELENI-

QMI PREDELA I NEPRERYWNOSTI FUNKCII y = f(x) W TO^KE a \PO kO[I",

TOGDA KAK FORMULIROWKI UTWERVDENIJ B) QWLQ@TSQ OPREDELENIQMI PREDELA I NEPRERYWNOSTI FUNKCII W TO^KE a \PO gEJNE".

pREDPRINQTAQ AWTOROM POPYTKA WYQSNITX STEPENX OBOSNOWANNOSTI \TOJ TERMINOLOGII OBNARUVILA SLEDU@]EE.

1.oPREDELENIQ PREDELA I NEPRERYWNOSTI FUNKCII PO PERWOMU SPO- SOBU | ^EREZ NERAWENSTWA S " I | WWEL W MATEMATI^ESKIJ OBIHOD wEJER[TRASS W SWOIH ZNAMENITYH (I UVE UPOMINAW[IHSQ NA S. 85) BER- LINSKIH LEKCIQH, STAW[IH POWOROTNYM PUNKTOM W RAZWITII MATEMA- TI^ESKOGO ANALIZA.

2.qWNO SFORMULIROWANNOGO OPREDELENIQ PREDELA FUNKCII W RABO- TAH kO[I NET. pRIWODIT ON (I NEODNOKRATNO POWTORQET) LI[X SLEDU- @]EE, WPOLNE TIPI^NOE DLQ MATEMATI^ESKOJ LITERATURY TOGO WREME-

NI, OPREDELENIE PREDELA PEREMENNOJ: \eSLI ZNA^ENIQ, POSLEDOWATELXNO PRIDAWAEMYE ODNOJ I TOJ VE PEREMENNOJ, NEOGRANI^ENNO PRIBLIVA@T- SQ K FIKSIROWANNOMU ZNA^ENI@ TAK, ^TO OTLI^IE OT NEGO STANOWITSQ SKOLX UGODNO MALYM, \TO POSLEDNEE ZNA^ENIE NAZYWA@T PREDELOM WSEH OSTALXNYH ... mY BUDEM OBOZNA^ATX PREDEL, K KOTOROMU SHODITSQ DAN-

112

NAQ PEREMENNAQ, ABREWIATUROJ lim , STAWQ EE PERED \TOJ PEREMENNOJ".1 dRUGOE DELO, ^TO PRI OBSUVDENII2 PREDELA KONKRETNOJ WELI^INY

f(x+ii);f (x) PRI STREMLENII i K NUL@3, ON DAL SLEDU@]EE TOLKOWANIE TOGO, KAK SLEDUET PONIMATX PREDEL \TOJ WELI^INY: \oBOZNA-

^IM " DWA O^ENX MALENXKIH ^ISLA, PERWOE WYBRANNOE TAKIM, ^TO DLQ ZNA^ENIJ i, ABSOL@TNAQ WELI^INA KOTORYH MENX[E, ^EM , OTNO[ENIE

f(x+ii);f (x) WSEGDA OSTAETSQ BOLX[IM, ^EM f0(x);", I MENX[IM, ^EM

f0(x)+"".4 lI[X BLAGODARQ wEJER[TRASSU \TO TOLKOWANIE STALO OPRE-

DELENIEM PREDELA FUNKCII W TO^KE (S SOHRANENIEM PO SEJ DENX UPO-

TREBLENIQ W EGO FORMULIROWKE TEH VE GRE^ESKIH BUKW " I ). sLEDUET OTMETITX, ^TO IZLAGAQ WY[EPRIWEDENNOE TOLKOWANIE, kO-

[I NIKAK NE OBOZNA^IL NI EGO NOWIZNY, NI SWOEGO AWTORSTWA, HOTQ BYL WESXMA ]EPETILEN W OTNO[ENII SWOEGO PRIORITETA W MATEMATI^ESKIH DOSTIVENIQH.

3. wZGLQD gEJNE5 NA PONQTIE NEPRERYWNOSTI FUNKCII W TO^KE (O PREDELE FUNKCII KAK TAKOWOM W EGO RABOTAH NI^EGO NET) QSEN IZ SLE- DU@]IH FRAGMENTOW EGO STATXI \|LEMENTY TEORII FUNKCIJ" (\Die Elemente der Functionenlehre") W \vURNALE ^ISTOJ I PRIKLADNOJ MA- TEMATIKI" (\Journal fur die reine und angewandte Mathematik") ZA 1872 G. (T. 74, S. 182):

1 w ORIGINALE (NAPRIMER, W [34], S. 4): \Lorsque les valeurs successivement attribuees a une m^eme variable s'approchent inde niment d'une valeur xe, de maniere a nir par en di erer aussi peu que l'on voudra, cette derniere est appelee la limite de toutes les autres ... Nous indiquerons la limite vers laquelle converge une variable donnee par l'abreviation lim placee devant cette variable".

2 w OPUBLIKOWANNOM W 1823 G. T. 1 EGO Resume des lec,ons donnees a l'Ecole Royale Polytechnique ([35], S. 44).

3 rAZUMEETSQ, i ZDESX SLUVIT U kO[I OBOZNA^ENIEM DEJSTWITELXNOJ

NIK I KOLLEGA SWOEGO BOLEE IMENITOGO SOOTE^ESTWENNIKA kANTORA.

113

\oPREDELENIE. fUNKCIQ f(x) NAZYWAETSQ NEPRERYWNOJ PRI OTDELXNOM KONKRETNO WZQTOM ZNA^ENII x = X , ESLI DLQ L@BOJ SKOLX UGODNO MALOJ ZADANNOJ WELI^INY " SU]ESTWUET TAKOE POLOVITELXNOE ^ISLO0 , ^TO NI DLQ KAKOJ POLOVITELXNOJ WELI^INY , MENX[EJ, ^EM 0, ABSOL@TNOE ZNA^ENIE WELI^INY f(X );f (X) NE PREWOSHODIT "".

i W SNOSKE NA \TOJ VE S. 182: \uTWERVDENIE, ^TO FUNKCIQ QWLQETSQ NEPRERYWNOJ W TOM I TOLXKO W TOM SLU^AE, KOGDA DLQ L@BOJ POSLE- DOWATELXNOSTI [x1 x2 I T. D., SHODQ]EJSQ] K X , WELI^INA f (X);f (xn) STANOWITSQ SKOLX UGODNO MALOJ, A TAKVE DOKAZATELXSTWO [\TOGO UTWERV- DENIQ] Q ZAIMSTWOWAL U G-NA kANTORA".1

4. tERMINY PREDEL (NEPRERYWNOSTX) \PO kO[I" I \PO gEJNE" WO-

[LI W OBIHOD SKOREE WSEGO POD WOZDEJSTWIEM AKAD. n.n. lUZINA2 , IDEI I UKAZANIQ KOTOROGO SFORMIROWALI STILX I TERMINOLOGI^ESKIE PRED- PO^TENIQ EGO U^ENIKOW, U^ENIKOW U^ENIKOW I IH PREEMNIKOW.

rAZUMEETSQ, USLOWNOSTX TEH ILI INYH TERMINOW I ^ASTOE IH NESOOT- WETSTWIE ISTORI^ESKOJ PRAWDE | DELO OBY^NOE NE TOLXKO W MATEMATIKE. w DANNOM VE SLU^AE UDIWLQET DRUGOE: TERMINOLOGIQ, NE POLU^IW[AQ PRIZNANIQ W AWTORITETNOJ MATEMATI^ESKOJ LITERATURE (W ^ASTNOSTI, EE NE UPOTREBLQET g.m. fIHTENGOLXC W [24]), PRODOLVAET AKTIWNO (ES- LI NE SKAZATX AGRESSIWNO) PROPAGANDIROWATXSQ ZAMETNOJ ^ASTX@ WU- ZOWSKIH PREPODAWATELEJ.

sTOIT OTMETITX, ^TO UTWERVDENIQ B)3 OBOIH KRITERIEW NE IME@T SIMWOLI^ESKOJ ZAPISI NA QZYKE L1Real, TAK KAK TREBU@T ZAPRE]ENNO- GO PRAWILAMI \TOGO QZYKA (SM. pRILOVENIE I) DEJSTWIQ KWANTORA PO PEREMENNOJ POSLEDOWATELXNOSTI (FUNKCII NATURALXNOJ PEREMENNOJ).

0 ist, der Zahlwerth von f (X );f (X) das " uberschreitet".

\Den Satz, dass die Function nur und immer continuirlich ist, wenn f(X);f(xn), fur jede Zahlenreiche von X beliebig klein wird, mit seinem Beweise, entlehne ich dem Herrn Cantor".

2 lUZIN nIKOLAJ nIKOLAEWI^ (1883{1950) | RUKOWODITELX MOSKOW- SKOJ [KOLY TEORII FUNKCIJ. oBSUVDAEMYE TERMINY MOVNO NAJTI W EGO U^EBNIKE DLQ PEDWUZOW [14].

3 w OTLI^IE OT UTWERVDENIJ a).

114

III.3. kAKOWY OB]IE SWOJSTWA FUNKCIJ, IME@]IH PREDEL

o TOM, NASKOLXKO \FFEKTIWNYM OKAZYWAETSQ PRIMENE-

NIE DOKAZANNYH KRITERIEW1 PREDELA I NEPRERYWNOSTI FUNK-

CII W TO^KE, MOVNO SUDITX PO DOKAZATELXSTWAM SLEDU@]IH UTWERVDENIJ.

PREDPOLOVITX, ^TO b = f(a), A c = g(a), TO \TO UTWERVDENIE PEREJDET W SLEDU@]EE.

eSLI FUNKCII y = f(x) I y = g(x) NEPRERYWNY W TO^KE a, TO FUNKCII y = f(x) g(x) I y = f(x) g(x), A ESLI g(a) 6=,0

TO I FUNKCIQ y = f(x) , TAKVE NEPRERYWNY W TO^KE a. g(x)

1 iLI, ESLI UGODNO, \KWIWALENTNYH OPREDELENIJ.

115

pEREHOD K PREDELU W NERAWENSTWAH

eSLI FUNKCII1 y = f(x) I y = g(x) IME@T PREDELY W TO^KE

fxng | L@BAQ SHODQ]AQSQ K TO^KE a POSLEDOWATELXNOSTX TO-

^EK, OTLI^NYH OT a. sOGLASNO KRITERI@ (\KWIWALENTNOMU OPREDELENI@) PREDELA FUNKCII POSLEDOWATELXNOSTI ff(xn)g

I fg(xn)g SHODQTSQ SOOTWETSTWENNO K ^ISLAM b I c, I DLQ WSEH ZNA^ENIJ n, NA^INAQ S NEKOTOROGO, WYPOLNQETSQ NERAWENST- WO f(xn) 6 g(xn). w SILU USTANOWLENNOGO RANEE (SM. S. 70) UTWERVDENIQ O NERAWENSTWAH DLQ PREDELOW POSLEDOWATELX- NOSTEJ WYPOLNQETSQ NERAWENSTWO b 6 c. Q.E.D.

sLEDU@]EE UTWERVDENIE ESTX ANALOG DLQ FUNKCIJ \PRIN- CIPA S\NDWI^A" DLQ POSLEDOWATELXNOSTEJ (SM. S. 71).

eSLI FUNKCII1 y = f(x) I y = g(x) IME@T OB]IJ PREDEL b W TO^KE a I W NEKOTOROJ OKRESTNOSTI \TOJ TO^KI2 WYPOL- NENY NERAWENSTWA f(x) 6 h(x) 6 g(x), TO SU]ESTWUET TAKVE

lim h(x) = b.

x!a

dOKAZATELXSTWO. pUSTX fxng | L@BAQ SHODQ]AQSQ K a

POSLEDOWATELXNOSTX TO^EK, OTLI^NYH OT a. tAK KAK W SILU

KRITERIQ PREDELA FUNKCII OBE POSLEDOWATELXNOSTI ff(xn)g

I fg(xn)g SHODQTSQ K ^ISLU b, PRI^EM f(xn) 6 h(xn) 6 g(xn) DLQ WSEH ZNA^ENIJ n, NA^INAQ S NEKOTOROGO, \PRINCIP S\NDWI- ^A" OBESPE^IWAET SHODIMOSTX POSLEDOWATELXNOSTI fh(xn)g K TOMU VE ^ISLU b. wTORI^NOE PRIMENENIE KRITERIQ PREDELA

FUNKCII POZWOLQET UTWERVDATX, ^TO lim h(x) = b. Q.E.D.

x!a

1 pRINIMA@]IE TOLXKO DEJSTWITELXNYE ZNA^ENIQ.

2 nEWAVNO, WKL@^AQ ILI NE WKL@^AQ SAMU \TU TO^KU.

116

lOKALXNYE OGRANI^ENNOSTX I SOHRANENIE ZNAKA

eSLI FUNKCIQ y = f(x) IMEET PREDEL W TO^KE a, TO SU]EST- WUET OKRESTNOSTX \TOJ TO^KI, W KOTOROJ DANNAQ FUNKCIQ QWLQETSQ OGRANI^ENNOJ1.

DENIE 8">0 9 >0 8x 0<jx;aj< )jf(x) ;bj<" . pO\TOMU,

WZQW KAKOE-LIBO ZNA^ENIE " > 0 I SU]ESTWU@]EE DLQ NEGO

POLOVITELXNOE ZNA^ENIE , MOVNO UTWERVDATX PO\TOMU: ESLI 0 < jx ; aj < , TO b ;jbj < f(x) < b + jbj, A SLEDOWATELXNO, f(x) >0 W SLU^AE b>0 I f(x)< 0 W SLU^AE b<0. Q.E.D.

wOT PRQMOE SLEDSTWIE DOKAZANNOGO UTWERVDENIQ.

eSLI FUNKCIQ3 y = f(x) QWLQETSQ NEPRERYWNOJ W TO^KE a I f(a) 6=,0TO SU]ESTWUET OKRESTNOSTX TO^KI a, W KOTOROJ ZNA^ENIQ FUNKCII QWLQ@TSQ POLOVITELXNYMI, ESLI f(a) >0, I OTRICATELXNYMI, ESLI f(a)< 0.

1 t. E. ZNA^ENIQ jf (x)j DLQ TO^EK x IZ \TOJ OKRESTNOSTI NE PREWOS- HODQT NEKOTOROGO POLOVITELXNOGO ^ISLA.

2 a ESLI FUNKCIQ OPREDELENA I W TO^KE a, TO jf (x)j < " + jbj+ jf(a)j

PRI jx;aj< .

3 pRINIMA@]AQ TOLXKO DEJSTWITELXNYE ZNA^ENIQ.

4 rASSMATRIWAEMAQ BEZ SAMOJ \TOJ TO^KI.

117

pREDEL I NEPRERYWNOSTX SLOVNOJ FUNKCII

eSLI FUNKCIQ x = '(t) IMEET W TO^KE PREDEL, RAWNYJ a,

A FUNKCIQ y = f(x) NEPRERYWNA W TO^KE a, TO KOMPOZICIQ

\TIH FUNKCIJ ILI, KAK ^ASTO GOWORQT, SLOVNAQ FUNKCIQ y = f('(t)) IMEET W TO^KE PREDEL, RAWNYJ f(a).

dOKAZATELXSTWO. sOGLASNO OPREDELENIQM (SM. S. 107, 101) PREDPOLOVENIQ O NEPRERYWNOSTI FUNKCII y = f(x) W TO^KE a I SU]ESTWOWANII PREDELA FUNKCII x = '(t) W TO^KE

OZNA^A@T ISTINNOSTX UTWERVDENIJ

O SU]ESTWOWANII U FUNKCII y = f('(t)) PREDELA W TO^KE , RAWNOGO f(a). Q.E.D.2

1 pO SHEME: DLQ L@BOGO ^ISLA " > 0 SU]ESTWUET (SOGLASNO PERWOMU UTWERVDENI@) ^ISLO >0 S WYPOLNENIEM IMPLIKACII

jx;aj< ) jf(x);f (a)j<",

A DLQ \TOGO ^ISLA , W SWO@ O^EREDX, SU]ESTWUET (UVE SOGLASNO WTOROMU UTWERVDENI@) ^ISLO >0 S WYPOLNENIEM IMPLIKACII

, 0<jt; j< )j'(t);aj< , = ( ) = ( ), . .

A SLEDOWATELXNO I WOZMOVNOSTX@ PODSTANOWKI x ' t W y f x T E OBRAZOWANIQ SLOVNOJ FUNKCII y = f('(t)), S WYPOLNENIEM IMPLIKACIJ

2 0<jt; j< )j'(t);, aj< )jf ('(t));f(a)j<". - wOT DRUGOE DOKAZATELXSTWO ISPOLXZU@]EE KRITERII PREDELA I NE

PRERYWNOSTI FUNKCII W TO^KE (SM. S. 109, 110). pUSTX ftng | L@BAQ SHODQ]AQSQ K POSLEDOWATELXNOSTX TO^EK tn, OTLI^NYH OT . wWIDU SU]ESTWOWANIQ U FUNKCII '(t) PREDELA W TO^KE , RAWNOGO a, POSLEDO- WATELXNOSTX f'(tn)g BUDET SHODITXSQ K a, A TAK KAK FUNKCIQ y = f(x) NEPRERYWNA W TO^KE a, POSLEDOWATELXNOSTX ff ('(tn))g BUDET SHODITXSQ K f(a).

118

sLEDU@]IJ PRIMER POKAZYWAET, ^TO USLOWIE NEPRERYWNOSTI FUNK- CII y =f(x) W TO^KE a NELXZQ OSLABITX, ZAMENIW EGO USLOWIEM SU]EST- WOWANIQ U FUNKCII PREDELA W \TOJ TO^KE.

NE QWLQETSQ NEPRERYWNOJ W TO^KE x=0, NO IMEET W NEJ PREDEL, RAWNYJ

NUL@. w SWO@ O^EREDX, FUNKCIQ x ='(t) IMEET W TO^KE t =0 PREDEL, RAW-

NYJ NUL@.1 wMESTE S TEM KOMPOZICIQ \TIH FUNKCIJ (SLOVNAQ FUNKCIQ) y = f('(t)) PREDELA W TO^KE t = 0 NE IMEET, POSKOLXKU DLQ SHODQ]EJSQ

119

III.4. ~TO NAZYWA@T FORMULAMI |JLERA I KAK ONI WYWODQTSQ

dLQ L@BOGO DEJSTWITELXNOGO ^ISLA t

dOKAZATELXSTWO. w SILU OPREDELENIQ ^ISLA eit (SM. S. 100),

SWOJSTW OPERACII KOMPLEKSNOGO SOPRQVENIQ (SM. S. 58) I TO-

lim zn = lim zn

NOSTI fzng KOMPLEKSNYH ^ISEL2, SPRAWEDLIWY RAWENSTWA:

it ; it (it)2 + (it)n ,

e = exp(it) = lim 1+ 1! + 2! + n!

n!+1

oKON^ATELXNO: jeitj2 = eiteit = eite;it = e0 = 1. Q.E.D.

iZ DOKAZANNOGO UTWERVDENIQ SLEDUET, ^TO DLQ L@BOGO DEJSTWITELXNOGO ^ISLA t ^ISLO eit IZOBRAVAETSQ TO^KOJ PLOSKOSTI C , LEVA]EJ NA EDINI^NOJ OKRUVNOSTI (OKRUV- NOSTI RADIUSA 1 S CENTROM W NA^ALE KOORDINAT). wOPROS O TOM, KAKOJ KONKRETNO TO^KOJ \TOJ OKRUVNOSTI IZOBRAVA- ETSQ ^ISLO eit, RAZRE[AETSQ SLEDU@]IM UTWERVDENIEM.

dLQ L@BOGO DEJSTWITELXNOGO ^ISLA t

arg(eit) = t (S TO^NOSTX@ DO SLAGAEMOGO, KRATNOGO 2 ) .

1 t. E. ^ISLOM, OBRATNYM PO OTNO[ENI@ K \KSPONENTE eit ^ISTO MNI-

MOGO ^ISLA it, SLUVIT KOMPLEKSNO SOPRQVENNOE S NEJ ^ISLO eit.

2 tAK KAK KOMPLEKSNOE SOPRQVENIE NA PLOSKOSTI C ESTX ZERKALXNOE OTRAVENIE OTNOSITELXNO DEJSTWITELXNOJ OSI, UTWERVDENIQ lim zn = z I lim zn = z, WYRAVAEMYE FORMULAMI

8" > 09n08n(n >n0 )jzn;.zj< ") I 8" >09n08n(n >n0 )jzn;zj< "),

QWLQ@TSQ \KWIWALENTNYMI

120

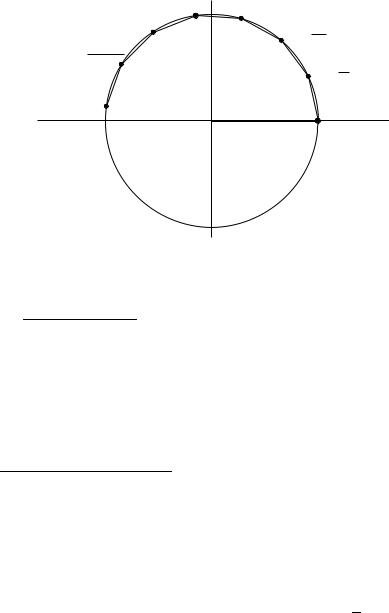
rIS. 6

dOKAZATELXSTWO. kAKIM BY NI BYLO NATURALXNOE ^ISLO n, KONCEWYE TO^KI WEKTOROW1, IZOBRAVA@]IH ^ISLA

(W \TOM PORQDKE), QWLQ@TSQ WER[INAMI PRAWILXNOJ n-ZWEN-

NOJ LOMANOJ, WPISANNOJ W EDINI^NU@ OKRUVNOSTX (RIS. 6)2. tAK KAK DLINA ODNOGO (PERWOGO) ZWENA \TOJ LOMANOJ RAWNA jexp itn ; 1j, DLINU ln WSEJ LOMANOJ MOVNO ZAPISATX W WIDE

1 wYHODQ]IH IZ NA^ALA KOORDINAT KOMPLEKSNOJ PLOSKOSTI.

2 tO, ^TO WSE \TI TO^KI LEVAT NA EDINI^NOJ OKRUVNOSTI, ESTX SLED-

n

ET, ^TO KAVDYJ POSLEDU@]IJ IZ IZOBRAVA@]IH \TI ^ISLA WEKTOROW KOMPLEKSNOJ PLOSKOSTI POLU^AETSQ POWOROTOM PREDYDU]EGO NA ODIN I TOT VE UGOL, RAWNYJ (POKA E]E NEIZWESTNOMU) arg exp itn .