
Шведенко Начала математического анализа 2011
.pdf
51 sTRANNOSTX SITUACII (PODME^ENNAQ kARDANO) SOSTOIT W
TOM, ^TO W SLU^AE, NAPRIMER, URAWNENIQ x3 |
; |
|
|
; |
|
p |
|
1 |
||
|
15x |
|
4 = 0 (U |
|||||||
KOTOROGO ESTX TRI DEJSTWITELXNYH |
KOR |
NQ x = 4 |
;2 |
|
3) |
|
||||
3 |
|
3 |
|
p121 |
|
|
|
|
||
FORMULA PRINIMAET WID x = q2 +p121 |
+q2 |
|
, T. E. W |
|||||||
WY^ISLENIQ WTORGAETSQ \NESU]ESTWU@]IJ" KWADRATNYJ KO- |
||||||||||
RENX IZ OTRICATELXNOGO ^ISLA. pOZDNEE WYQSNILOSX, \TO QW- LENIE WOZNIKAET WSQKIJ RAZ, KOGDA URAWNENIE x3 + px+ q = 0 IMEET TRI (RAZLI^NYH) DEJSTWITELXNYH KORNQ.
pOSKOLXKU UJTI OT WOZNIKA@]EGO ZATRUDNENIQ | NEOB- HODIMOSTI OPERIROWATX \NESU]ESTWU@]IMI" ^ISLAMI | NI- KAK NE UDAWALOSX, RE[ILI POSTUPITX TRADICIONNYM SPOSO- BOM: ESLI KAKOE-LIBO NEUDOBNOE QWLENIE NELXZQ USTRANITX, EGO SLEDUET LEGALIZOWATX. dLQ \TOGO DOSTATO^NO BYLO PRI- NQTX PRAWILA SOWMESTNYH DEJSTWIJ2 S NASTOQ]IMI (\DEJ- STWITELXNYMI") ^ISLAMI I \NESU]ESTWU@]IM" ^ISLOM p1 , KOTOROE SO WREMENEM STALI NAZYWATX MNIMOJ EDINICEJ I OBO- ZNA^ATX i. sUTX \TIH PRAWIL SWODITSQ K TOMU, ^TO OPERIRO- WATX S MNIMOJ EDINICEJ i SLEDUET TAK VE, KAK PRI OBRA]E- NII S MNOGO^LENAMI OPERIRU@T S DEJSTWITELXNOJ PEREMEN- NOJ, NO S ZAMENOJ WS@DU i2 NA ;1.
pERWYM SLOWO \MNIMYJ" (\imaginaire") PO OTNO[ENI@ K KORNQM URAWNENIJ PRIMENIL dEKART W SWOEJ \gEOMETRII" [38, S. 63]. oBOZNA- ^ENIE i WWEL |JLER (W RUKOPISI 1777 G.), NO AKTIWNO WNEDRQTX NA^AL (S 1801 G.) gAUSS3 WNEDRENIE [LO POSTEPENNO, I NEKOTORYE DO SIH POR
WMESTO i PI[UT p;1. |LEKTROTEHNIKI, PRIWYK[IE WOSPRINIMATX i
KAK SILU TOKA, OBOZNA^A@T MNIMU@ EDINICU j.
1 hOTQ \NASTOQ]IMI" TOGDA S^ITALI LI[X POLOVITELXNYE KORNI. 2 nA^ALO OFORMLENI@ \TIH PRAWIL POLOVIL ITALXQNSKIJ MATEMA- TIK I INVENER-GIDRAWLIK bOMBELLI (Bombelli Ra aele, 1526{1573) W
SWOEJ \aLGEBRE" (\L'Algebra"), WY[ED[EJ W 1572 G.
3 Gauss Carl Friedrich (1777{1855) | NEMECKIJ MATEMATIK, FIZIK,
ASTRONOM I GEODEZIST.

52
sKLADYWAQ I PEREMNOVAQ (UKAZANNYM SPOSOBOM) DEJST- WITELXNYE ^ISLA a b : : : I MNIMU@ EDINICU i, POLU^A@T
SO^ETANIQ1 WIDA a + bi, KOTORYE (I W \TOM SOSTOIT IH ZA- ME^ATELXNOE SWOJSTWO) OBLADA@T PRIWY^NYMI ATRIBUTAMI
^ISEL: IH MOVNO SKLADYWATX, WY^ITATX, PEREMNOVATX I DELITX, POLU^AQ W REZULXTATE TAKIE VE SO^ETANIQ:
(a+bi) (c+di) = a+bi c di = (a c) + (b d)i,
(a+bi)(c+di) = ac+bic+adi+bidi = (ac;bd) + (ad+bc)i,
a+bi = (a+bi)(c;di) = ac+bic;adi;bidi = ac+bd + bc;ad i c+di (c+di)(c;di) cc+dic;cdi;didi cc+dd cc+dd
(DELENIE W PREDPOLOVENII c+di6= 0,KOGDA cc+dd6= 0).
sO^ETANIQ a+ bi DEJSTWITELXNYH ^ISEL I MNIMOJ EDI-
NICY POLU^ILI NAZWANIE KOMPLEKSNYH ^ISEL. wMESTE ONI OB-
RAZU@T SISTEMU KOMPLEKSNYH ^ISEL C , RAZDELQ@]U@ S SIS- TEMOJ DEJSTWITELXNYH ^ISEL R SWOJSTWA, WYRAVAEMYE AK-
SIOMAMI2 w TERMINAH ALGEBRY \TO OZNA^AET: SISTEMA KOMPLEKSNYH ^ISEL (TAK VE KAK I SISTE- MA DEJSTWITELXNYH ^ISEL) QWLQETSQ POLEM.
kASATELXNO VE SWOJSTW DEJSTWITELXNYH ^ISEL, WYRAVA- EMYH AKSIOMAMI A7{A10, TO PRI PEREHODE K KOMPLEKSNYM ^ISLAM ONI UTRA^IWA@T SMYSL, POSKOLXKU (I \TO NEOBHODI-
MO OTMETITX I POD^ERKNUTX) W SISTEME KOMPLEKSNYH ^ISEL
OTNO[ENIQ \BOLX[E" I \MENX[E" NE OPREDELENY3.
1 s WOZMOVNOSTX@ PERESTANOWKI W NIH KAK SLAGAEMYH, TAK I SOMNO- VITELEJ, I ZAPISX@ a;bi WMESTO a+(;b)i. ~ASTNYMI SLU^AQMI TAKIH
SO^ETANIJ QWLQ@TSQ DEJSTWITELXNYE ^ISLA I SO^ETANIQ WIDA bi.
2 s TEM, ODNAKO, OTLI^IEM, ^TO DLQ KOMPLEKSNYH ^ISEL \TI SWOJSTWA BUDUT UVE NE AKSIOMAMI, A TEOREMAMI, WYTEKA@]IMI IZ \TIH AKSIOM
DLQ DEJSTWITELXNYH ^ISEL.
3 pOPYTKA WWESTI IH PRIWODIT K PROTIWORE^IQM S PRIWY^NYMI SWOJSTWAMI \TIH OTNO[ENIJ. dOSTATO^NO POPROBOWATX UWQZATX L@BOE IZ PREDPOLOVENIJ i>0 I i< 0 S AKSIOMAMI A7 I A8.

53
tERMIN \KOMPLEKSNYE ^ISLA" BYL WWEDEN gAUSSOM W WOS- PROIZWODIMOM ZDESX FRAGMENTE EGO RABOTY 1831 G. [40, Bd. II, S. 102]. oT^ETLIWO WIDNO, ^TO gAUSS OB_EDINQL \TIM TERMI-
NOM1 DEJSTWITELXNYE I MNIMYE ^ISLA, WOSPRINIMAQ DEJST- WITELXNOE ^ISLO KAK ^ASTNYJ SLU^AJ ^ISLA KOMPLEKSNOGO
(A NE NE^TO EMU PROTIWOPOLOVNOE).
a+bi SODERVIT:
I . dEJSTWITELXNYE ^ISLA, U KOTORYH b = 0, I SREDI NIH,
W ZAWISIMOSTI OT TOGO, KAKOWO a,
1)NULX,
2)POLOVITELXNYE ^ISLA,
3)OTRICATELXNYE ^ISLA.
II . mNIMYE ^ISLA, U KOTORYH b 6=.0zDESX SNOWA RAZLI- ^A@T:
1) MNIMYE ^ISLA BEZ DEJSTWITELXNOJ ^ASTI, T. E. TE, U KOTORYH a= 0,
2) MNIMYE ^ISLA S DEJSTWITELXNOJ ^ASTX@ U KOTORYH I b 6=,0I a 6=.0
pERWYE PRI VELANII MOVNO NAZYWATX ^ISTO MNIMYMI ^ISLAMI, A WTORYE SME[ANNYMI MNIMYMI ^ISLAMI"2.
1 kOTORYJ WMESTE S PRO^IMI TERMINAMI, RAZ_QSNENNYMI W \TOM FRAGMENTE, STALI OB]EPRINQTYMI.
2 w LATINSKOM ORIGINALE:
\Campus numerorum complexorum a+bi continet
I. numeros reales, ubi b=0, et, inter hos, pro indole ipsius a
1)cifram
2)numeros positivos
3)numeros negativos
II. numeros imaginarios, ubi b cifrae inaequalis. Hic iterum distinguutur
1)numeri imaginarii absque parte reali, i. e. ubi a=0
2)numeri imaginarii cum parte reali, ubi neque b neque a=0.
Priores si placet numeri imaginarii puri, posteriores numeri imaginasrii mixti vocari possunt."

54
iRLANDSKIJ MATEMATIK gAMILXTON1 NA S. 12 WY[ED[EJ W 1853 G. MONOGRAFII [42] (W KOTOROJ OKON^ATELXNO OFORMILOSX PONQTIE WEKTO- RA) PREDLOVIL SLEDU@]U@ INTERPRETACI@ KOMPLEKSNYH ^ISEL:
\The more general expression of algebra, a1+p;1a2 , for any (so called) imaginary root of a quadratic or other equation, ... interpreted as being a symbol of the number-couple which I had otherwise denoted by (a1 a2) , ...
its multiplication by another number-couple is expressed by the formula
(b1 b2)(a1 a2)=(b1a1 ;b2 a2 b2 a1 +b1a2)."
w REZULXTATE [IROKO RASPROSTRANILOSX OPREDELENIE KOMPLEKSNYH ^ISEL KAK UPORQDO^ENNYH PAR DEJSTWITELXNYH ^ISEL S UMNOVENIEM
PO PREDSTAWLENNOJ FORMULE I POKOORDINATNYM SLOVENIEM. tAK KAK DEJSTWITELXNOE ^ISLO ESTX ^ASTNYJ SLU^AJ ^ISLA KOMPLEKSNOGO (SM. S. 53), PRINQTIE \TOGO OPREDELENIQ, WYNUVDAET SDELATX NE UKRA[A@-
]IJ MATEMATIKU WYWOD: DEJSTWITELXNOE ^ISLO | \TO PARA DEJSTWI- TELXNYH ^ISEL.
dLQ KRATKOJ ZAPISI KOMPLEKSNYH ^ISEL ISPOLXZU@T OD- NOBUKWENNYE OBOZNA^ENIQ (NAPRIMER, c= a+bi a= 1;ip2)2. nAIBOLEE ^ASTO (OSOBENNO DLQ OBOZNA^ENIQ KOMPLEKSNYH PE- REMENNYH) ISPOLXZU@T ZAPISX z = x+iy (A TAKVE w = u+iv). dEJSTWITELXNYE ^ISLA x I y W ZAPISI KOMPLEKSNOGO ^ISLA z = x+iy NAZYWA@T SOOTWETSTWENNO DEJSTWITELXNOJ
I MNIMOJ ^ASTQMI \TOGO KOMPLEKSNOGO ^ISLA S OBOZNA^E-
NIQMI x = Rez y = Imz. rAWENSTWO KOMPLEKSNYH ^ISEL z = x+iy I w = u+iv RAWNOSILXNO RAWENSTWU KAK DEJSTWI-
TELXNYH, TAK I MNIMYH IH ^ASTEJ: z = w , x= u I y = v.3
zAPISX z = x+iy = x 1+y i NAWODIT NA MYSLX NAGLQDNO PREDSTAWLQTX KOMPLEKSNYE ^ISLA z KAK TO^KI (ILI WEKTO-
RY4) DEKARTOWOJ KOORDINATNOJ PLOSKOSTI R2 c KOORDINATA-
1 Hamilton William Rowan, 1805{1865.
2 w PERWOM SLU^AE a PREDPOLAGAETSQ DEJSTWITELXNYM ^ISLOM, A WO WTOROM | SLUVIT OBOZNA^ENIEM MNIMOGO.
3 iZ PREDPOLOVENIQ, ^TO x+iy =u+iv PRI x6=u ILI y 6=v , SLEDOWALO
BY, ^TO i | DEJSTWITELXNOE ^ISLO: i = x;u ILI i= y;v .
v;y x;u

55
MI x = Rez y = Imz. eDINICA 1 I MNIMAQ EDINICA i OBRE- TA@T PRI \TOM SMYSL EDINI^NYH NAPRAWLQ@]IH WEKTOROW
OSEJ x (\DEJSTWITELXNOJ") I y (\MNIMOJ"), A SLOVENIE I
WY^ITANIE KOMPLEKSNYH ^ISEL | SLOVENIQ I WY^ITANIQ
IZOBRAVA@]IH IH WEKTOROW.
k NAGLQDNOMU IZOBRAVENI@ KOMPLEKSNYH ^ISEL OBRATILISX LI[X SPUSTQ DWA S POLOWINOJ WEKA POSLE IH WOZNIKNOWENIQ: DOLGOE WREMQ IH WOSPRINIMALI ISKL@^ITELXNO KAK \FANTOMY", WOZNIKA@]IE W HODE RE[ENIQ URAWNENIJ I IS^EZA@]IE NA ZAWER[A@]EM \TAPE.
pERWYMI GEOMETRI^ESKOE PREDSTAWLENIE KOMPLEKSNYH ^ISEL DA-
LI NORWEVSKIJ TOPOGRAF wESSELX1, IZOBRAZIW[IJ 1 I p;1 EDINI^NYMI PERPENDIKULQRNYMI DRUG K DRUGU WEKTORAMI2 PLOSKOSTI I UKAZAW[IJ PRAWILO PEREMNOVENIQ KOMBINACIJ a+bp;1 \TIH WEKTOROW, I FRAN- CUZSKIJ MATEMATIK aRGAN3, TAKVE PREDSTAWLQW[IJ KOMPLEKSNYE ^ISLA
\NAPRAWLENNYMI OTREZKAMI" (\lignes dirigees").
iZOBRAVATX KOMPLEKSNYE ^ISLA TO^KAMI PLOSKOSTI NA^AL gAUSS. w 1811 G. (E]E DO WWEDENIQ TERMINA \KOMPLEKSNYE ^ISLA") ON PISAL:
\tAK VE KAK SOWOKUPNOSTX WSEH DEJSTWITELXNYH WELI^IN MOVNO MYS- LITX W WIDE BESKONE^NOJ PRQMOJ LINII, SOWOKUPNOSTX WSEH WELI^IN, DEJSTWITELXNYH I MNIMYH, MOVNO PREDSTAWITX W WIDE BESKONE^NOJ PLOSKOSTI, GDE KAVDAQ TO^KA, ZADAWAEMAQ ABSCISSOJ a I ORDINATOJ b, PREDSTAWLQET WELI^INU a+bi"4.
1 Wessel Caspar (1745{1818) W 1797 G. W DOKLADE dATSKOJ KOROLEWSKOJ AKADEMII. w 1999 G. WY[LO ANGLIJSKOE IZDANIE \TOGO DOKLADA [55], SODERVA]EE PODROBNOE VIZNEOPISANIE wESSELQ, A TAKVE ISTORI^ESKIJ O^ERK O KOMPLEKSNYH ^ISLAH I IH GEOMETRI^ESKOM PREDSTAWLENII.
2 wO WREMENA wESSELQ TERMINOM \WEKTOR" E]E NE OPERIROWALI, I U NEGO GOWORITSQ O PRQMYH LINIQH.
3 Argand Jean-Robert (1768{1822) W KNIGE [31], WPERWYE WY[ED[EJ
(ANONIMNO) W 1806 G.
4 w NEMECKOM ORIGINALE [40, Bd. VIII, S. 90{91]: \so wie man sich das ganze Reich aller reellen Grossen durch eine unendliche gerade Linie denken kann, so kann man das ganze Reich aller Grossen, reellen und imaginarer Grossen sich durch eine unendliche Ebene sinnlich machen, worin jeder Punkt, durch Abscisse = a, Ordinate = b bestimmt, die Grosse a+bi gleichsam reprasentirt."

56
uQSNITX GEOMETRI^ESKIJ SMYSL UMNOVENIQ I DELENIQ KOMPLEKSNYH ^ISEL (^EGO RAZGLQDYWANIEM FORMUL NA S. 52 DOSTI^X TRUDNO) POZWOLQET PEREHOD OT DEKARTOWYH KOORDI- NAT NA PLOSKOSTI K POLQRNYM r ', SWQZANNYM S DEKARTOWY- MI RAWENSTWAMI x= r cos ' y = r sin '.
l@BOE NENULEWOE KOMPLEKSNOE ^ISLO z = x+iy PRINIMAET TOGDA WID z = r(cos '+ i sin '), KOTORYJ NAZYWA@T POLQRNOJ
(ILI TRIGONOMETRI^ESKOJ) FORMOJ \TOGO KOMPLEKSNOGO ^IS-
LA, PRI \TOM r NAZYWA@T MODULEM, A ' | ARGUMENTOM ^ISLA z S OBOZNA^ENIQMI IH r = jzj ' = arg z.1 gEOMETRI^ESKI MO- DULX KOMPLEKSNOGO ^ISLA z 6= 0ESTX DLINA IZOBRAVA@]EGO EGO WEKTORA KOORDINATNOJ PLOSKOSTI A ARGUMENT | WELI- ^INA UGLA2, OBRAZUEMOGO \TIM WEKTOROM S OSX@ x. mODULX L@BOGO KOMPLEKSNOGO ^ISLA z = x+iy ODNOZNA^NO NAHODITSQ IZ RAWENSTWA jzj2 = x2 + y2 (T. E. jzj = px2 + y2), ARGUMENT VE, NAPROTIW, OPREDELQETSQ LI[X S TO^NOSTX@ DO SLAGAEMO- GO, KRATNOGO 2 , I EDINOGO RAWENSTWA DLQ EGO WY^ISLENIQ (^EREZ x I y) NE SU]ESTWUET3.
pRI IZOBRAVENII KOMPLEKSNYH ^ISEL z1
PLOSKOSTI WELI^INA jz1;z2j PRIOBRETAET SMYSL RASSTOQNIQ MEVDU \TIMI TO^KAMI. mNOVESTWO TEH z 2 C , DLQ KOTORYH jz ;z1j = jz ;z2j, ESTX PO\TOMU PRQMAQ, PERPENDIKULQRNAQ K
1 ~ISLO 0 ARGUMENTA (A SLEDOWATELXNO, I POLQRNOJ FORMY) NE IME-
def
ET, TOGDA KAK j0j = 0.
2 zA WELI^INU UGLA (W RADIANNOJ MERE) PRINIMAETSQ DLINA DUGI EDI-
NI^NOJ OKRUVNOSTI, WYSEKAEMAQ \TIM UGLOM, WZQTAQ SO ZNAKOM + ILI ;, SOOTWETSTWENNO OTS^ETU DUGI OT OSI x \PROTIW HODA ^ASOWOJ STRELKI" ILI VE W PROTIWOPOLOVNOM NAPRAWLENII (DOPUSKAETSQ PRIBAWLENIE K IZMERENNOJ DLINE DUGI L@BOGO KRATNOGO DLINY OKRUVNOSTI, T. E. 2 ).
3 rAWENSTWO arg z = arctg xy (+2 k), WERNO LI[X DLQ KOMPLEKSNYH
^ISEL z = x + iy S x > 0, TOGDA KAK PRI x < 0 DEJSTWUET RAWENSTWO arg z = arctg xy + (+2 k).
57
OTREZKU, SOEDINQ@]EMU TO^KI z1 I z2 , I PROHODQ]AQ ^EREZ EGO SEREDINU.1 oKRUVNOSTX RADIUSA r S CENTROM z0 ESTX
MNOVESTWO TEH TO^EK z 2C , DLQ KOTORYH |
jz |
;z0j = r.2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
iZWESTNYE NERAWENSTWA DLQ STORON TREUGOLXNIKA (\DLI- |
|||||||||||||||||||||||||||||||||||||||||
NA L@BOJ STORONY TREUGOLXNIKA NE BOLX[E SUMMY I NE MENX- |
|||||||||||||||||||||||||||||||||||||||||
[E RAZNOSTI DLIN DWUH DRUGIH STORON") IME@T SLEDU@]U@ |
|||||||||||||||||||||||||||||||||||||||||
ZAPISX ^EREZ MODULI KOMPLEKSNYH ^ISEL: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
jjz1j;jz2jj |
6 jz1 + z2j 6 jz1j |
+ jz2j. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
wOT PRIMERY POLQRNOJ ZAPISI KOMPLEKSNYH ^ISEL: |
|
|
|||||||||||||||||||||||||||||||||||||||
1 = cos 0+i sin 0 |
;2 = 2(cos +i sin ) |
i= cos |
|
+i sin |
|
, |
|||||||||||||||||||||||||||||||||||
2 |
2 |
||||||||||||||||||||||||||||||||||||||||
p |
|
+i= 2 cos |
|
+i sin |
|
|
|
|
p |
|
+i= 2 cos |
5 |
+i sin |
5 |
|
|
|
||||||||||||||||||||||||
3 |
|
, |
|
3 |
, |
|
|
||||||||||||||||||||||||||||||||||
|
6 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
1+i= p |
|
|
|
6 |
|
|
|
|
|
|
;i= p |
|
|
; |
|
|
|
|
6 |
|
|
|
|
|
6 |
|
|
|
|
||||||||||||
|
cos |
|
+i sin |
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
3. |
|||||||||||||||||||||
2 |
|
|
, 1 |
2 |
|
|
+ i sin |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
; |
4 |
|
|
|
4 |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
; 4 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
;4 |
|
|
|
|
|
|
|
2 ). |
||||||||||||||
(WOZMOVNO DOBAWLENIE K ARGUMENTAM L@BOGO KRATNOGO |
|||||||||||||||||||||||||||||||||||||||||
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
; |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|||||||||||
zAPISX KOMPLEKSNYH ^ISEL W POLQRNOJ FORME SRAZU VE PROQSNQET GEOMETRI^ESKIJ SMYSL IH UMNOVENIQ I DELENIQ:
ESLI z = r(cos '+i sin '), A w = (cos |
+i sin |
), TO |
||||||||||||||||||
zw = r(cos '+i sin ') (cos +i sin ) = |
|
|||||||||||||||||||
|
|
|
= r (cos ' cos |
;sin ' sin |
|
)+i(sin ' cos +cos ' sin ) = |
||||||||||||||
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
= r cos('+ |
)+i sin('+ ) |
|||
|
z |
= |
|
r(cos '+i sin ') |
(cos ' |
; |
i sin ') |
; |
|
|||||||||||
|
w |
(cos +i sin |
) |
|
|
|
|
|
|
|
|
|
= |
|
||||||
|
|
|
|
(cos ;i sin ) |
|
|
||||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
(cos ' cos |
+sin ' sin |
)+i(sin ' cos ;cos ' sin ) = |
||||||||||||||
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
r |
|
;cos('; )+i sin('; ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||
|
|
1 |
nERAWENSTWO VE |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
jz ;z1j < jz ;z2j OPISYWAET TU IZ DWUH POLUPLOS- |
|||||||||||||||||
KOSTEJ, OGRANI^ENNYH UKAZANNOJ PRQMOJ, KOTORAQ SODERVIT TO^KU z1 . |
||||||||||||||||||||
|
|
2 oGRANI^ENNYJ VE \TOJ OKRUVNOSTX@ KRUG OPISYWAETSQ NERAWEN- |
||||||||||||||||||
STWOM jz;z0j< r. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
3 rAWENSTWO 1;i =p2;cos |
4 |
;i sin |
4 |
TOVE WERNO, NO ONO NE QWLQETSQ |
||||||||||||||
ZAPISX@ ^ISLA 1;i W POLQRNOJ FORME. |
|
|
||||||||||||||||||

58
wYWODY:
1. pRI PEREMNOVENII NENULEWYH KOMPLEKSNYH ^ISEL IH MODULI PEREMNOVA@TSQ, A ARGUMENTY SKLADYWA@TSQ1:
jzwj= jzjjwj arg(zw) = arg z+arg w
GEOMETRI^ESKI \TO OZNA^AET:
PRI UMNOVENII KOMPLEKSNOGO ^ISLA z 6= 0NA KOMPLEKSNOE ^ISLO w 6= 0WEKTOR, IZOBRAVA@]IJ ^ISLO z, IZMENQET DLI- NU W jwj RAZ I POWORA^IWAETSQ (WOKRUG NA^ALA KOORDINAT) NA UGOL, RAWNYJ arg w:
2. mODULX OTNO[ENIQ DWUH NENULEWYH KOMPLEKSNYH ^I- SEL RAWEN OTNO[ENI@ IH MODULEJ, A ARGUMENT | RAZNOSTI
IH ARGUMENTOW: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
z |
= |
jzj |
, |
arg |
z |
= arg z |
; |
arg w. |
|||||
|
|
w |
|
||||||||||||
|
|
|
j |
w |
j |
|
w |
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
3. sPRAWEDLIWA |
FORMULA mUAWRA |
|
|
|
|
||||||||||
|
|
|
|
. |
|||||||||||
|
|
|
|||||||||||||
|
;r(cos '+i sin ') n = rn(cos n'+i sin n') n2Z |
|
|||||||||||||
|
|
|
|||||||||||||
|
|
|
|||||||||||||
~ISLA x+ iy I x;iy |
(ILI, ^TO TO VE SAMOE, x+ i(;y)) |
||||||||||||||
NAZYWA@T KOMPLEKSNO SOPRQVENNYMI S OBOZNA^ENIQMI IH z I z. nA PLOSKOSTI KOMPLEKSNO SOPRQVENNYM ^ISLAM SOOT-
WETSTWU@T TO^KI (WEKTORY), SIMMETRI^NYE OTNOSITELXNO OSI x. kAK SLEDSTWIQ, IME@T MESTO RAWENSTWA:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
z = z z w = z w zw = z w |
|
|
w |
= |
|
, |
||||||||||||||||||||||||||
|
|
|
|
|
w |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z+ |
|
|
z; |
|
|
|||||||||||||||||||||
|
|
|
= z |
|
|
|
|
|
2 |
z |
= Re z |
z |
= Im z. |
||||||||||||||||||||||
|
z |
zz |
= z |
||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|||||||||||||||||||||||||||||||
j j |
|
j j |
|
|
|
|
j j |
|
|
|
|
|
|
|
|
|
|
|
2i |
|
|
|
|
|
|
|
|
||||||||
1 wSE RAWENSTWA DLQ ARGUMENTOW S^ITA@TSQ WYPOLNENNYMI S TO^- NOSTX@ DO SLAGAEMOGO, KRATNOGO 2 .
2 De Moivre Abraham (1687{1754) | FRANCUZSKIJ MATEMATIK. o TOM,
KAKIM SLOVNYM PUTEM I W KAKOM WIDE BYLA WYWEDENA IM (W 1730 G.) \TA FORMULA, MOVNO PRO^ITATX W PRIME^ANII K x138 PERWOGO TOMA TRUDA
59
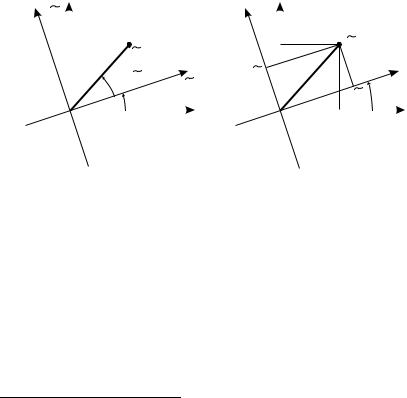
pRIMEROM PRILOVENIQ PRAWIL PEREMNOVENIQ KOMPLEKS- NYH ^ISEL MOVET SLUVITX WYWOD FORMUL PREOBRAZOWANIQ DEKARTOWYH KOORDINAT NA PLOSKOSTI PRI POWOROTE OSEJ.
|
|
|
|
e e |
|
|
|
|||
|
pUSTX OSI KOORDINAT x y |
POWERNUTY OTNOSITELXNO OSEJ |
||||||||
x y (WOKRUG IH OB]EGO NA^ALA) NA UGOL (RIS. 3). |
||||||||||
|
i y |
|
iy |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
z |
|
|
|
iy |
z |
||
|
|
|
|
|
|
|
||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
arg z |
x |
|
i y |
|
|
|
|
|
|
|
|
|
|
x |
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
x |
0 |
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
rIS. 3
pROIZWOLXNO WZQTAQ TO^KA PLOSKOSTI IMEET PRI \TOM
|
|
e e |
|
DWA NABORA DEKARTOWYH KOORDINAT: (x y) I (x y), A POTOMU |
|||
WEKTOR, WEDU]IJ IZ NA^ALA KOORDINAT W \TU TO^KU, SLUVIT |
|||
IZOBRAVENIEM SRAZU DWUH KOMPLEKSNYH ^ISEL (NA DWUH \K- |
|||
|
|
|
e e e |
ZEMPLQRAH KOMPLEKSNOJ PLOSKOSTI): z = x + iy I |
z = x + iy, |
||
e |
|
e |
|
DLQ KOTORYH jzj = jzj, A arg z = arg z + . wYPOLNQETSQ PO\-
x+ iy = (x + iy) (cos + i sin ),
TOMU RAWENSTWO e e IZ KOTOROGO (SRAWNENIEM DEJSTWITELXNYH I MNIMYH ^ASTEJ) I POLU^A@T FORMULY PREOBRAZOWANIQ DEKARTOWYH KOORDINAT PRI POWOROTE OSEJ (NA UGOL ):
(x = x cos ; y sin
y = xe sin + yecos :
e e
60
I.4. kAK IZWLEKA@T KORNI
IZ KOMPLEKSNYH ^ISEL
kORNQMI n-J STEPENI (n 2 N) IZ KOMPLEKSNOGO ^ISLA a
NAZYWA@T WSE TE KOMPLEKSNYE ^ISLA, KOTORYE UDOWLETWORQ- @T URAWNENI@ zn = a. dLQ IH OBOZNA^ENIQ (WSEH WMESTE I
KAVDOGO W OTDELXNOSTI) ISPOLXZU@T OBOZNA^ENIQ a1 I pn a.
n
pOSKOLXKU (W SILU PRAWILA PEREMNOVENIQ KOMPLEKSNYH
n |
6 |
= 0I zn = 0 NESOWMESTIMY, EDINSTWEN- |
||||||
^ISEL) RAWENSTWA z |
|
|||||||
NYM ZNA^ENIEM p |
|
QWLQETSQ 0. |
||||||
0 |
||||||||
w SLU^AE VE a 6= 0PEREHOD W URAWNENII zn = a K POLQR- |
||||||||
NOJ ZAPISI a = jaj(cos + i sin ) I z = r(cos ' + i sin ') (S |
||||||||
NEIZWESTNYMI POKA |
r I ') PREOBRAZUET EGO W RAWENSTWO |
|||||||
rn(cos n'+i sin n') = jaj(cos +i sin ), |
||||||||
RAWNOSILXNOE SLEDU@]IM DWUM: |
||||||||
p |
|
|
|
k |
|
|||
r = n |
jaj ' = |
n |
+2 |
n |
k 2Z. |
|||
tAK KAK PERE^ISLENNYM ZNA^ENIQM ' OTWE^A@T ROWNO |
||||||||
n LU^EJ, WYHODQ]IH IZ NA^ALA KOORDINAT I RAZDELQ@]IH PLOSKOSTX NA n UGLOW RASTWORA 2n , SLEDUET WYWOD:
dLQ L@BOGO NENULEWOGO KOMPLEKSNOGO ^ISLA a SIMWOL pn a IMEET ROWNO n KOMPLEKSNYH ZNA^ENIJ. iZOBRAVENNYE NA KOORDINATNOJ PLOSKOSTI, ONI RASPOLAGA@TSQ W WER[INAH PRAWILXNOGO n-UGOLXNIKA, WPISANNOGO W OKRUVNOSTX RADI- USA r = pn jaj S CENTROM W NA^ALE KOORDINAT.1
|TOT WYWOD DAET GEOMETRI^ESKIJ SPOSOB NAHOVDENIQ WSEH ZNA^ENIJ pn a, ESLI IZWESTNO HOTQ BY ODNO IZ NIH. nAPRIMER,
;i ESTX ODNO IZ ZNA^ENIJ p6 ;1, A OSTALXNYE NAHODQTSQ PO- STROENIEM PRAWILXNOGO [ESTIUGOLXNIKA, WPISANNOGO W EDI- NI^NU@ OKRUVNOSTX, S ODNOJ IZ WER[IN ;i (RIS. 4, a).
1 pOD pn jaj ZDESX PONIMAETSQ ARIFMETI^ESKIJ (POLOVITELXNYJ) KO- RENX STEPENI n IZ POLOVITELXNOGO ^ISLA jaj (SM. S. 33).
