После подстановки значения скорости потока в последнее уравнение получим .
Безразмерное отношение
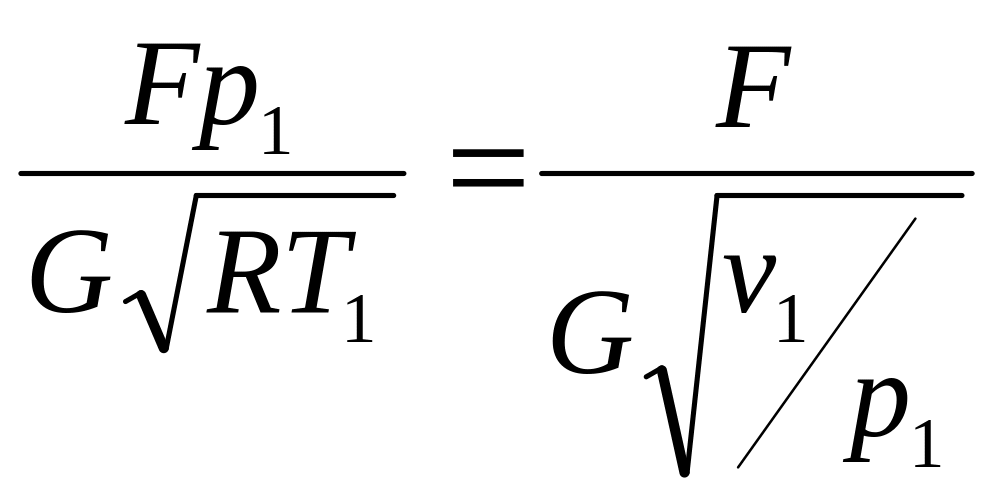(14.11)
назовем параметром площади.
На рис. 14.4 представлена зависимость
параметра скорости и параметра площади
в функции
.
Как видно из графика, кривая изменения
параметра площади показывает, что
последняя в начале уменьшается. Это
объясняется тем, что скорость растет
быстрее, чем удельный объем. Так
продолжается до сечения, в котором
,
где устанавливается критическое
давление, а скорость принимает значение
скорости звука. При дальнейшем построении
этой кривой по формуле (14.11) параметр
площади, а следовательно, и площадь
поперечного сечения будет увеличиваться,
а вместе с ней для этих сечений будет
расти и значение параметра скорости по
формуле (14.10).
Расширяющаяся часть сопла Лаваля
создает условия для получения
сверхзвукового потока, которые не могут
быть созданы только понижением давления
в среде, куда происходит истечение.
Расчет комбинированного сопла сводится
к определению проходных сечений сопла
и
,
при заданном расходе
и угле расширения сопла
,
который обеспечит безотрывное течение
газа.
Сопло Лаваля позволяет использовать любые перепады давления, получать большую располагаемую работу и скорость истечения газа, большую скорости звука.
Истечение при наличии трения
Одно из особых явлений возникает в
сопле Лаваля, если давление среды
повысится по сравнению с расчетным
.
Из опытов известно, что даже при
незначительном увеличении
расширение газа в раструбе прекращается
в некотором промежуточном сечении.
После этого наступает резкое повышение
давления – скачок уплотнения. С
увеличением величины противодавления
интенсивность скачка возрастает, а
промежуточное сечение приближается к
критическому. Естественно, что
возникновение скачка уплотнения
сопровождается переходом изоэнтропного
течения в течение с возрастанием
энтропии.
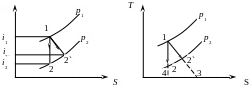
Рис. 14.5. iS и TS – диаграммы
В реальных условиях на полученные закономерности влияет внутреннее и внешнее (о стенки) трение газа. Из-за действия сил трения происходит диссипация (рассеяние) механической энергии и превращение части ее в теплоту, в результате чего внутренняя энергия, энтальпия и энтропия движущегося газа возрастают. Этот процесс можно изобразить на iS – диаграмме в виде линии 1-2`. Нужно помнить, что изображение необратимой адиабаты является условным, поскольку в диаграмме состояния в принципе могут изображаться только кривые обратимых процессов. Теплота трения при отсутствии теплообмена с окружающей средой усваивается потоком газа, при этом часть теплоты трения идет на работу расширения и преобразуется в энергию движения газа (пл. 122` на TS – диаграмме). Остальная часть представляет собой потерю работы (кинетической энергии) и изображается пл. 2`243. Вся теплота трения, выделившаяся в потоке, равна пл. 12`341.
Из iS – диаграммы
видно, что тепловой перепад
при наличии трения меньше, а следовательно
и скорость истечения, определяемая по
формуле (14.2) будет меньше, чем в случае
трения без сопротивления. Точный
теоретический учет влияния вязкости
невозможен, поэтому прибегают к помощи
эмпирических коэффициентов. Потеря
энергии, вызываемая внутренними
сопротивлениями, определяется по формуле
,
где
- коэффициент потери энергии.
Если обозначить
- коэффициент скорости, причем
,
то
,
.
Для хорошо обработанных и спрофилированных
сопел величина
лежит в пределах 0,95 – 0,98. Т.к. действительная
кинетическая энергия газового потока
будет меньше теоретической
,
то используют также понятие коэффициента
полезного действия сопла:
.
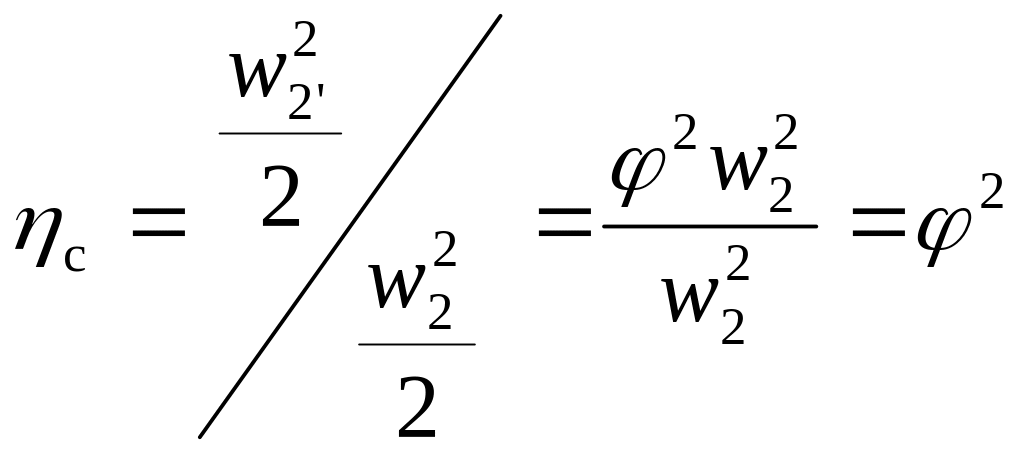Понятно, что неучет вязкости газа, его теплопроводности, диффузии и т.п. позволяет значительно упростить основные уравнения газовой динамики и их решения. Однако при определенных условиях это приводит к большим погрешностям. Поэтому в специальных работах приводятся различные теории и методы, позволяющие в той или иной степени учесть эти явления.