
- •Введение
- •Термодинамические параметры состояния
- •2. Основные понятия и определения
- •Идеальный газ. Законы идеального газа
- •Закон Бойля – Мариотта
- •Закон Гей – Люссака
- •Закон Шарля
- •3. Уравнение состояния идеального газа
- •Закон Авогадро
- •Молярная масса
- •4. Уравнение менделеева – клапейрона
- •Уравнение состояния реальных газов
- •5. Газовые смеси
- •6. Первое начало термодинамики Теплота и работа
- •Принцип эквивалентности
- •7. Внутренняя энергия
- •Закон сохранения и превращения энергии
- •Формулировки первого начала термодинамики
- •Виды работ
- •Развернутое уравнение первого закона термодинамики и его частные выражения
- •Энтальпия
- •8. Теплоемкость газов
- •9. Анализ термодинамических процессов на основании I начала термодинамики Понятие об энтропии
- •Схемы распределения энергии
- •Изотермический процесс
- •Адиабатный процесс
- •10. Политропные процессы
- •Группы политропных процессов
- •Способы определения n
- •Связь между n и с
- •11. Второе начало термодинамики Односторонность протекания самопроизвольных процессов
- •Формулировки второго начала термодинамики
- •Выражение первого закона термодинамики для циклов
- •Термический коэффициент полезного действия прямого цикла
- •12. Цикл карно
- •Термодинамическая шкала температур
- •Математическое выражение второго закона термодинамики
- •Критика учения о «тепловой смерти вселенной»
- •13. Термодинамика потока газа. Основные понятия и уравнения гидрогазодинамики
- •Уравнение неразрывности
- •Уравнение энергии – уравнение первого закона термодинамики
- •Уравнение состояния идеального газа
- •Уравнение импульса
- •Располагаемая работа газа в потоке
- •Скорость звука и критические параметры
- •14. Скорость и расход газа при течении. Истечение из сужающихся сопел
- •Переход через скорость звука. Сопло Лаваля
- •После подстановки значения скорости потока в последнее уравнение получим .
- •Истечение при наличии трения
- •Дросселирование газа
- •15. Термодинамика химических процессов
- •Термохимические процессы
- •Первый закон термодинамики применительно к химическим процессам
- •Закон Гесса
- •Второй закон термодинамики
- •Тепловой закон Нернста
- •16. Циклы поршневых двигателей внутреннего сгорания
- •Цикл со смешанным подводом тепла
- •Цикл с подводом тепла при постоянном объеме
- •Цикл с подводом тепла при постоянном давлении
- •Сравнение циклов поршневых двс
- •Сравнение по условию .
- •Сравнение по условию
- •17. Циклы компрессоров
- •Многоступенчатые компрессоры
- •Центробежный компрессор
- •Осевой компрессор
- •18. Циклы газотурбинных установок
- •Регенеративные циклы
- •19. Циклы паросиловых установок
- •Цикл Карно для водяного пара
- •Цикл Ренкина
- •Цикл с промежуточным перегревом пара
- •Регенеративный цикл
- •Бинарные циклы
- •Цикл парогазовой установки
- •Теплофикационный цикл
- •20. Циклы холодильных установок
- •Цикл воздушной холодильной машины
- •Цикл парокомпрессорной холодильной машины
- •Цикл теплового насоса
- •Детандеры
- •21. Реактивные двигатели
- •Цикл ПуВрд
- •Цикл трд
- •22. Ракетные двигатели
- •Цикл рдтт
- •Цикл жрд
- •Цикл ярд
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
Переход через скорость звука. Сопло Лаваля
Приведенные соотношения справедливы при равномерном распределении скоростей в выходном сечении сопла. Последнее же зависит от его профиля и формы среза.
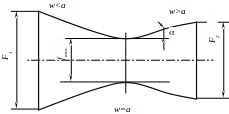
Рис. 14.3. Сопло Лаваля
Если же сопло имеет косой срез (для
придания нужного направления потоку
газа), т.е. его выходное сечение не
перпендикулярно оси сопла, то при
![]() истечение газа происходит со сверхзвуковой
скоростью. При этом газ в суживающейся
части сопла ускоряется до скорости
звука, а у выхода из сопла расширяется,
приобретая скорость, большую скорости
звука (угол поворота струи зависит от
истечение газа происходит со сверхзвуковой
скоростью. При этом газ в суживающейся
части сопла ускоряется до скорости
звука, а у выхода из сопла расширяется,
приобретая скорость, большую скорости
звука (угол поворота струи зависит от
![]() ).
Сопла с косым срезом применяют для
относительно небольшого увеличения
скорости сверх критической. Для еще
большего увеличения скорости истечения
выше критической применяют комбинированное
сопло, состоящее из суживающейся и
расширяющейся частей. Впервые было
предложено в 80-х годах прошлого столетия
шведским инженером, изобретателем
Лавалем. Разрез сопла Лаваля изображен
на рис. 14.3.
).
Сопла с косым срезом применяют для
относительно небольшого увеличения
скорости сверх критической. Для еще
большего увеличения скорости истечения
выше критической применяют комбинированное
сопло, состоящее из суживающейся и
расширяющейся частей. Впервые было
предложено в 80-х годах прошлого столетия
шведским инженером, изобретателем
Лавалем. Разрез сопла Лаваля изображен
на рис. 14.3.
Суживающаяся часть работает при дозвуковой скорости, а расширяющаяся при сверхзвуковой скорости. В наименьшем сечении сопла Лаваля скорость потока равна местной скорости звука. Соответствующим подбором величины выходного сечения сопла добиваются того, чтобы давление в выходном сечении сопла было равно давлению среды . Такой режим называется расчетным. Кинетическая энергия в этом случае будет эквивалентна полному адиабатному теплоперепаду между давлениями и и скорость истечения вычисляется по формуле (14.2). Таким образом, максимальный расход через сопло Лаваля остается таким же, как и в суживающемся сопле, увеличивается только скорость газа.
Расчет суживающейся части сопла Лаваля проводится точно так же, как и для обычного дозвукового сопла. Площадь минимального сечения сопла определяется по заданному уравнением (14.9).
Скорость газа на выходе из сопла Лаваля определяется уравнением (14.2), а для идеального газа – уравнением (14.1).
Площадь выходного сечения сопла
определяется из уравнения
![]() .
.
Величина удельного объема газа в
выходном сечении сопла
для случая идеального газа может быть
найдена из уравнения адиабаты по
известным величинам
,
и
 .
.
Длина суживающейся части сопла, как и
длина всякого дозвукового сопла,
выбирается минимальной. Расширяющаяся,
сверхзвуковая часть сопла, имеющая
обычно коническую форму, имеет такую
длину, чтобы угол раствора сопла
![]() не превышал 12 – 14.
При больших углах раствора возникает
опасность отрыва потока от стенок сопла
и расширение газа в нем сопровождается
образованием вихрей точно так же, как
и при отсутствии раструба. Профилированием
проточной части сопла достигается лишь
различное распределение давлений внутри
сопла, но расход при этом в выходном
сечении всегда остается постоянным.
не превышал 12 – 14.
При больших углах раствора возникает
опасность отрыва потока от стенок сопла
и расширение газа в нем сопровождается
образованием вихрей точно так же, как
и при отсутствии раструба. Профилированием
проточной части сопла достигается лишь
различное распределение давлений внутри
сопла, но расход при этом в выходном
сечении всегда остается постоянным.
Рассмотрим изменение скорости и площади
поперечного сечения в зависимости от
изменения давления по длине сопла. Для
удобства анализа воспользуемся формулами
(14.1) и (14.4) и представим их в безразмерном
виде. Для этого скорость потока
 ,
поделим на
,
поделим на
![]() .
.
Безразмерное отношение
![]() , (14.10)
, (14.10)
назовем параметром скорости.
Расход газа через сопло равен
![]() .
.
Умножим и поделим правую часть равенства
на
![]() ,
тогда
,
тогда
![]() .
.
Т.к. связь между давлением и температурой
может быть определена по уравнению
адиабаты для изоэнтропного течения
газа, то
![]() .
.
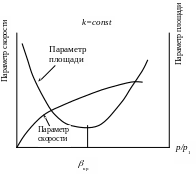
Рис. 14.4. Зависимость параметра скорости и параметра площади
