Изотермический процесс

Так называется процесс, протекающий при постоянной температуре ТРТ. Уравнение изотермы в p – координатах находится из уравнения Клапейрона; поскольку RT – величина постоянная, имеемp = const т.е. изотерма в p – координатах изображается равнобокой гиперболой (симметричной относительно осей координат).

Чем выше температура, тем больше p и тем дальше от начала координат располагается изотерма.

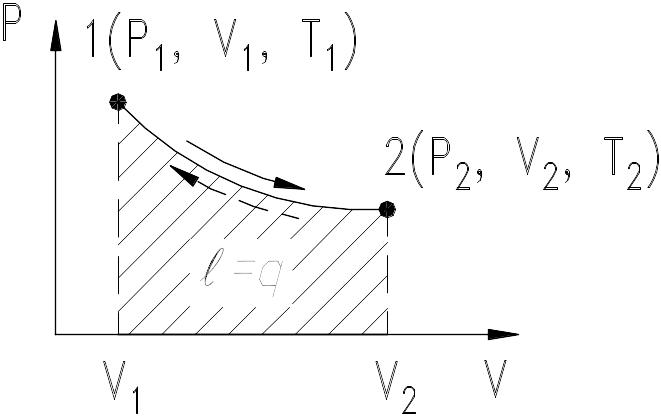
Рис. 9.11. Изотермический процесс

В TS – координатах изотерма представляет собой горизонтальную прямую, а уравнение ее Т=const. Связь между параметрами находится как следствие того, что p остается неизменным, т.е. p_{1 1} = p_{2 2} или , т.е. давление в изотермическом процессе обратно пропорционально объему (закон Бойля-Мариотта).

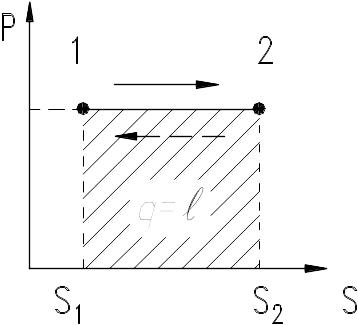
Рис. 9.12. Изотермический процесс в ps – координатах

Работа изотермиеского процесса .

Заменив p на из уравнения Клапейрона и проинтегрировав, получим .

С помощью уравнения Клапейрона и соотношения p_{1 1} = p_{2 2} формулу можно записать в следующих видах , , .

Т.к. температура постоянна, то U = c_V dT = 0, i = c_P dT= 0.

Вычисление приращений энтропии в изотермическом процессе упрощается: .

Из при T₁=T₂ имеем .

Схема распределения энергии

Поскольку U =0, то тепло изотермического процесса равно работе ( q=l) и оно может быть подсчитано по любой из формул.

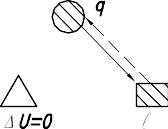
Рис. 9.13. Схема распределения энергии

С другой стороны, , т.е. тепло изотермического процесса выражается площадью прямоугольника в TS – координатах. Из схемы видно, что все подведенное тепло в изотермическом процессе идет на работу расширения, в случае сжатия идеального газа вся затраченная работа преобразуется в теплоту, отводимую от него, а коэффициент распределения тепла

Адиабатный процесс

Называется (от греческого - непереходимый) процесс, на любом элементарном участке которого отсутствует теплообмен с внешней средой, т.е. dq=0. Следствием этого условия, является также и отсутствие теплообмена во всем процессе (q= о). В полной мере обеспечить отсутствие теплообмена, между ТРТ и окружающей средой не представляется возможным. Однако при достаточно хорошей тепловой изоляции ТРТ от внешней среды, или когда процесс протекает столь быстро, что теплоотдача, зависящая от времени, не успевает существенно повлиять на ход изменения состояния, процесс практически будет адиабатным (отклонение от равновесного процесса учитывают­ся в дальнейшем введением в расчеты специального коэффициента). Последнее, однако, не может служить определением адиабатного процесса, поскольку не исключает случаев, когда подвод тепла на одном участки процесса компенсируется отводом на другом участке.

Кроме того, следует обратить внимание на то, что условие dq=0 не означает, что q=const, ибо dq не является полным дифференциалом. Следовательно, вообще говорить о постоянстве теплоты бессмысленно, т.к. теплота является не функцией состояния, а функцией процесса.

Уравнение адиабаты в - координатах можно вывести на основе уравнения первого закона термодинамики .

Дифференциал dT находится из уравнения состояния: . После преобразо­ваний с использованием уравнений и , получаем , , , , .

После интегрирования для произвольного конечного процесса 1-2 имеем , откуда , или .

Поскольку точки 1 и 2 взяты произвольно, то вообще - уравнение адиабаты Пуассона в - координатах. Т.к. k > 1 , то адиабата в - координатах представляет собой неравнобокую гиперболу, имеющую большую крутизну по сравнению с изотермой. Поскольку dq =0, то ds=0 и s=const , т.е. энтропия в адиабатном процессе постоянна.

Следовательно, уравнением адиабаты в Тs- коорди­натах будет s=const, и графически адиабата представляется вертикальной линией. Иными словами, обратимый адиабатный процесс является в то же время изоэнтропным процессом. Необратимый адиабатный процесс не является изоэнтропным. Например, течение реального газа в шероховатой трубе, снабженной идеальной теплоизоляцией. Т.к. в таких условиях всегда будет присутствовать диссипация (рассеяние) энергии потока, то этот процесс будет необратим и проходить с повышением энтропии системы. Соотно­шение между давлением и объемом в адиабатном процессе уже было получено .

Рис. 9.14. Графическое представление адиабаты

Умножая обе части равенства на и используя после несложных преобразований, получим соотношение между температурой и объемом в адиабатном процессе:

(9.8)

Определив из и подставив в (9.8), найдем соотношение между температурой и давлением в адиабатном процессе:

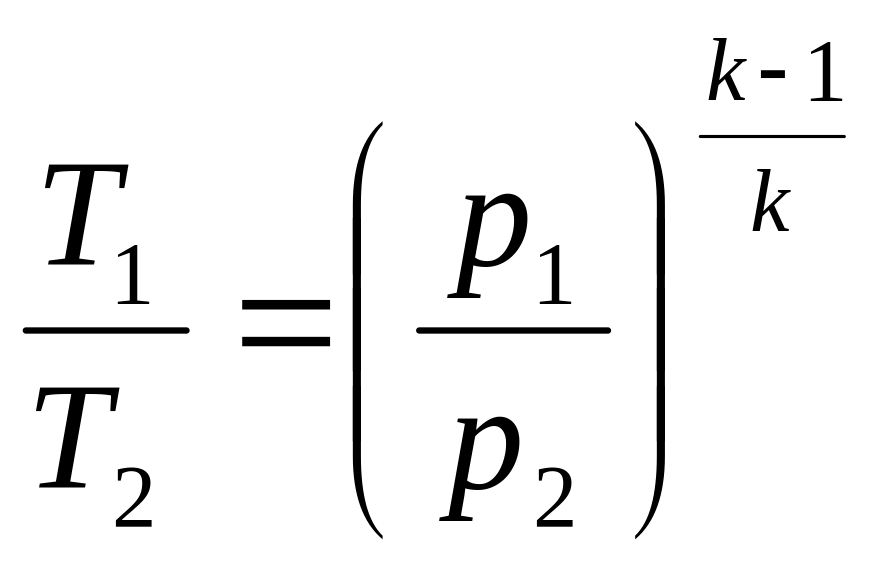. (9.9)

Эти соотношения исчерпывают возможные связи между основными параметрами p, и T в адиабатном процессе.

Работа адиабатного процесса находится интегрированием по общей формуле

, Дж/кг. (9.10)

После подстановок и преобразований .

Используя и , можно получить из последнего выражения, другие, применяющиеся в расчетах, выражения работы адиабатного процесса: ; ; .

Т.к. dq=0 и q=0, то из dq=du+pd следует, что u=-pd =-l, т.е. работа адиабатного процесса осуществляется за счет уменьшения внутренней энергии газа. Другими словами, при адиабатном расширении производимая газом работа осуществляется вследствие уменьшения его внутренней энергии (p и T понижаются). При адиабатном сжатии затраченная внешняя работа идет на увеличение внутренней энергии газа (p и T повышаются).

Рис. 9.15. Схема распределения энергии

Коэффициент распределения тепла .