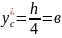3.6.1. Пример решения задачи № 1. Расчет консольной балки
Для деревянной консольной балки, расчетная схема которой дана на рис. 22, а, требуется:
подобрать из условия прочности по допускаемым напряжениям размеры и в прямоугольного поперечного сечения (рис. 18,б), приняв в,
а =1 м, допускаемое напряжение для дерева на растяжение = 10 МПа, а допускаемое напряжение при сдвиге [τ]= 5 МПа.
проверить жесткость спроектированной балки, считая допускаемое значение прогиба сечения А равным 1/300 её длины, а E=1∙104 МПа.
Расчетные значения
нагрузок:
,
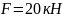М=25 кН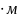
,
.
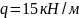Решение
1. Определение вида расчета
По условию задачи требуется подобрать размеры поперечного сечения балки, т.е. требуется выполнить проектный расчет. Из условия прочности по нормальным напряжениям проектный расчет выполняется по соотношению
.
Поскольку значение
допускаемого напряжения
задано,
то для выполнения расчета следует
знать
.
Для проверки
прочности по касательным напряжениям
необходимо знать
.
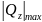Для определения
и
строим эпюры
и
.
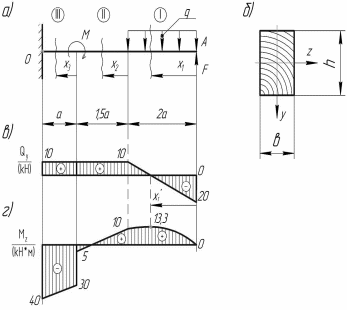
Рис. 22. Расчетная схема балки (а), сечение балки (б),
эпюры поперечных сил (в) и изгибающих моментов (г)
2. Построение эпюр и
а) Определяем реакции опор
Обычно построение эпюр и начинают с определения реакций опор. В данной задаче балка консольная, поэтому нет необходимости определять реакции опор, так как эпюры и можно построить, двигаясь от свободного конца к заделке и рассматривая отсеченную правую часть, на которую не наложены связи.
б) Разбиваем балку на участки
Используя правило, изложенное в разделе 2.1, разбиваем балку на три участка.
в) Записываем аналитические выражения и по участкам
Рассекая
балку на каждом из участков произвольным
сечением, координаты которых обозначены
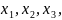и
рассматривая каждый раз отсеченную
правую часть балки, записываем выражения
и
по участкам
Участок I:
;
.
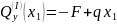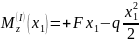Анализируя
полученные выражения, приходим к выводу,
что поперечная сила
изменяется по линейной зависимости, а
изгибающий момент – квадратичная
функция координаты
.
Определим значения
и
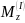в граничных сечениях I
участка:
при
;
;
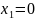
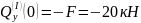при
;
.
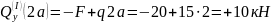Так как поперечная
сила
на первом участке, меняя знак в одном
из сечений (обозначим его координату
)
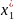, обращается в нуль (см. рис. 22,в), то в
соответствии со следствием 3 из
дифференциальных зависимостей (1.3)
изгибающий момент в этом сечении будет
иметь локальный экстремум. Приравнивая
выражение
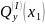нулю, определим координату
этого сечения:
,
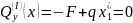отсюда
.
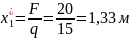Подставляя значение
в выражение
,
находим экстремальное значение
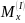на первом участке. Это будет локальный
максимум
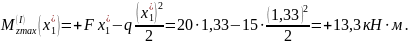
Переходим к рассмотрению участка II.
Участок
II:
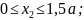
Рассматривая отсеченную правую часть, получим
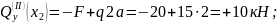
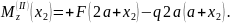
Таким образом,
поперечная сила во всех сечениях второго
участка постоянна и равна +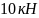
,
а изгибающий момент – линейная функция
координаты
.
Для построения эпюры
на втором участке определим значения
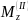в граничных сечениях этого участка.
При
;
при
.
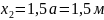
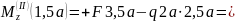
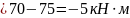Участок
III:
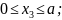
Рассматривая по-прежнему отсеченную правую часть, получим:
;
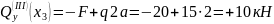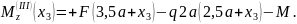
Как и на участке
II,
поперечная сила на участке III
постоянна во всех его поперечных сечениях
(т.к. не зависит от координаты
),
а изгибающий момент – линейная
функция координаты
.
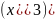Для построения эпюры
на участке III
определим значения изгибающего момента
в граничных сечениях этого участка.
При
;
.
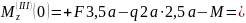
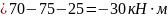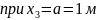
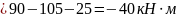г) Строим эпюры и , располагая их строго под схемой балки (рис. 22, в, г).
Для построения эпюры проводим нулевую линию эпюры параллельно оси балки. Положительные значения откладываем выше нулевой линии, а отрицательные – ниже (рис. 22, в).
Для построения эпюры проводим нулевую линию параллельно оси балки. Положительные значения откладываем выше нулевой линии, а отрицательные – ниже (рис. 22, г).
д) Проводим проверку правильности построения эпюр и
При анализе правильности построения эпюр с учетом следствий из дифференциальных зависимостей между Мz, Qy и q (3.3) отмечаем:
– на участках, где отсутствует q (участки II и III), поперечная сила Qy– постоянна, а изгибающий момент изменяется по линейному закону;
– на участке, где имеется равномерно распределенная нагрузка интенсивностью q, поперечная сила Qy изменяется по линейному закону, а изгибающий момент – по закону квадратной параболы, с выпуклостью направленной навстречу действия q;
– на эпюре Qy имеются скачки в сечениях, где приложены сосредоточенная сила F=20 кН и опорная реакция заделки;
– на эпюре Мz
имеются скачки там, где приложены внешний
сосредоточенный момент
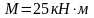и
реактивный момент заделки.
Все это позволяет сделать вывод, что эпюры построены правильно и могут быть использованы при дальнейшем решении задачи.
3. Подбор размеров поперечного сечения
Из эпюры
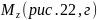следует, что
,
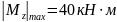следовательно,
.
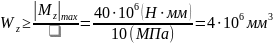Осевой момент сопротивления для прямоугольного сечения при заданном соотношении сторон ( в) определяется по формуле
.
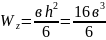Приравнивая
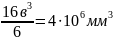найдем размер в:
;
в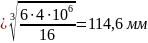
.
Округляя в большую сторону, примем
в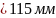
,
.
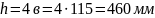Проверим прочность подобранного сечения по нормальным напряжениям:
.
.
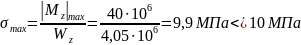Прочность по нормальным напряжениям обеспечена. Недонапряжение в 1% объясняется округлением размера сечения в в большую сторону.
4. Проверка прочности по касательным напряжениям
Поскольку балка изготовлена из дерева, то проверка прочности по касательным напряжениям является обязательной.
Для проверки прочности по касательным напряжениям используем условие (3.13):
.
Из эпюры поперечных сил (см.рис. 22, в) следует, что
.
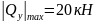Для прямоугольного
сечения
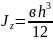с учетом соотношения
в
получим
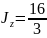в.
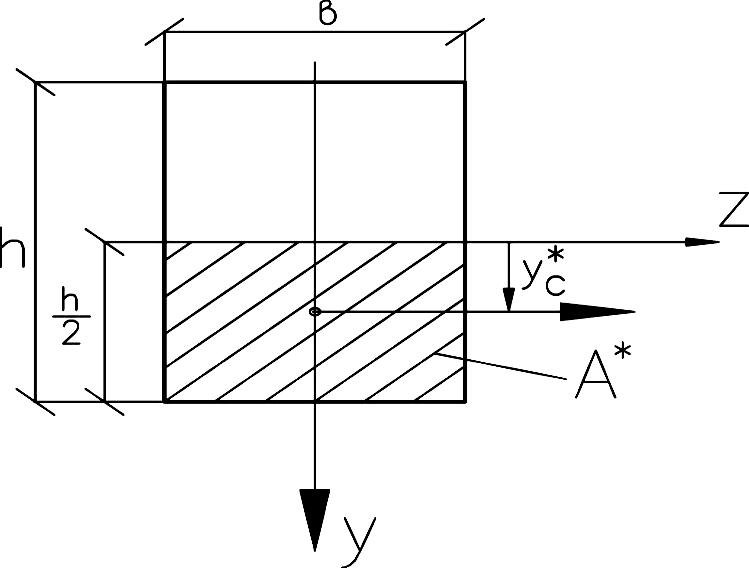
Наибольшие касательные напряжения для прямоугольного сечения возникают в точках, лежащих на главной и центральной оси , так как для половины сечения максимален, а в(y) = в = Const (рис. 23).
Рис. 23. Схема сечения балки |
.
|
;
;
Таким
образом,
,
а максимальные касательные напряжения
.
Приходим к выводу, что прочность по касательным напряжениям обеспечена с большим запасом.
Окончательно принимаем следующие размеры поперечного сечения:
в
;
h=
46 см.
5. Проверка выполнения условия жесткости
Согласно условию задачи, для данной балки условие жесткости имеет вид:
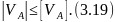
Для определения
воспользуемся методом начальных
параметров
1. Выбираем систему координат. Начало координат помещаем в заделку, ось x направляем слева направо, ось y - вниз (рис. 24).
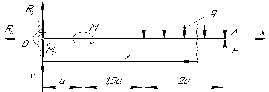
Рис. 24
Отбрасывая
заделку, заменим ее реакциями
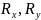и реактивным моментом
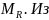уравнений статики определим реакции
связей:
.
.
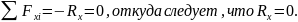
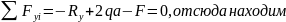
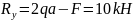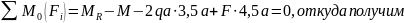
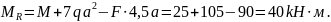
Проверим правильность определения реакций:
Следовательно, реакции найдены верно.
2. Составление универсального уравнения упругой линии балки. Запишем выражение изгибающего момента для произвольного сечения участка балки, наиболее удаленного от начала координат:
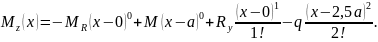
Тогда универсальное уравнение упругой линии балки будет иметь вид
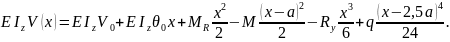
3. Определение
начальных параметров.
Для определения начальных параметров
воспользуемся граничными условиями в
заделке, где прогиб и угол поворота
равны нулю, т.е.
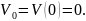Таким
образом, универсальное уравнение упругой
линии балки приводится к виду
.
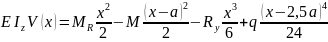4. Вычисление прогиба сечения А. Для этого сечения x =4,5 a =4,5 м.
Подставляя в уравнение упругой линии получим:
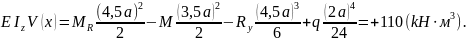
Для подобранного прямоугольного поперечного сечения
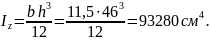
Тогда прогиб сечения А
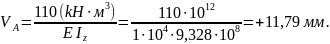
Знак «+» говорит о том, что сечение А перемещается по направлению оси y, т.е. вниз.
5) Проверка
выполнения условия жесткости. По
условию
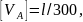где l
– длина
балки. Так как l
= 4,5 a
= 4,5 м, то
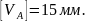
Сравнение
показывает, что VA<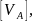
следовательно, условие жесткости
выполняется, что позволяет окончательно
принять размеры сечения, полученные из
условия прочности, т.е. принимаем
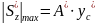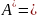
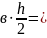
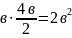