3.2. Определение напряжений

При плоском (прямом) поперечном изгибе в поперечных сечениях балки возникают нормальные 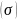и касательные 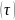напряжения.

Нормальные напряжения вызваны изгибающим моментом и определяются по формуле

,

(3.4)

где – величина изгибающего момента в сечении (алгебраическая); – ордината точки, в которой определяется ; 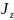– момент инерции поперечного сечения балки относительно нейтральной оси .

Из соотношения (3.4) видно, что нормальные напряжения линейно зависят от координаты и достигают наибольших значений в точках сечения, наиболее удаленных от нейтральной линии. График, изображающий закон изменения нормальных напряжений по высоте сечения, называемый эпюрой напряжений, показан на рис. 16, а.

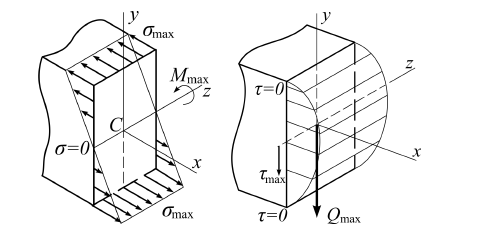а) б)

Рис. 16. Эпюры нормальных и касательных напряжений

Касательные напряжения в сечении балки при плоском поперечном изгибе возникают от поперечной силы и определяются по формуле Д.И. Журавского:

,

(3.5)

где – поперечная сила в сечении; - статический момент относительно нейтральной оси площади сечения, расположенной выше или ниже точки, в которой определяются касательные напряжения ; в – ширина сечения на уровне точки, в которой определяется касательное напряжение .

В отличие от нормальных напряжений распределение касательных напряжений по высоте поперечного сечения зависит от формы сечения. Для прямоугольного сечения эпюра имеет форму сектора окружности (см. рис. 16,б) и описывается уравнением

.

Из него следует, что касательные напряжения достигают максимального значения в точках сечения, расположенных на нейтральной оси (аналогично и для остальных форм сечений).

Отметим, что σ_max и τ_max действуют в различных точках сечения: σ_max на периферии, в точках, наиболее удаленных от нейтральной оси, где τ_max ‒ в центре, на нейтральной линии, где σ =0. Сравнительный анализ показывает, что для длинных балок (ℓ > 5h) τ_max существенно меньше σ_max. Это позволяет в большинстве случаев не принимать во внимание касательные напряжения и проводить расчет на прочность как при чистом, так и при поперечном изгибе только по нормальным напряжениям.

3.3. Расчеты на прочность

3.3.1. Расчет по допускаемым напряжениям

Для балок в большинстве практических случаев определяющими являются нормальные напряжения, а касательные напряжения играют второстепенную роль. Поэтому основным принимается условие прочности по нормальным напряжениям.

Анализ формулы (3.4) и эпюры напряжений (рис. 16,а.) позволяет записать условие прочности по нормальным напряжениям при плоском изгибе для балок из пластичных материалов в виде

.
или ,	(3.6)
где .	(3.7)

Здесь – осевой момент сопротивления сечения;

– расстояние от нейтральной линии (ось z) до наиболее удаленной точки сечения, взятое по модулю;

. –допускаемое напряжение материала по пределу текучести.

Для балок из хрупких материалов, когда допускаемые напряжения материала балки на растяжение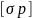 и на сжатие не равны (т.е. ) между собой, условие прочности записывают отдельно для растянутой и сжатой зоны поперечного сечения:

;	(3.8)
,	(3.9)
где ; .	(3.10)

В формулах (3.9) величины 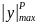и – взятые по модулю расстояния от нейтральной линии сечения до наиболее растянутого и наиболее сжатого волокна.

Из условий прочности ( 3.6), (3.8) и (3.9) выполняют три вида расчетов:

Проверочный расчет. Он заключается в проверке выполнения условий (3.6), (3.8) и (3.9) при заданных нагрузках, материале балки, форме и размерах поперечного сечения.

Проектный расчет. Его цель – подбор поперечного сечения балки при заданных нагрузках и материале балки. Из условия прочности определяют требуемое значение осевого момента сопротивления, принимая . .

Например, для балки из пластичного материала из (3.6) получим

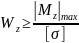. (3.11)

По значению и известной форме сечения определяют его размеры или подбирают номер стандартного прокатного профиля из таблицы сортамента.

Расчет грузоподъемности. Цель этого расчета – определение максимальных значений нагрузок, которые могут быть приложены к балке, при заданных: материале балки, форме и размерах поперечного сечения, а также схеме приложения нагрузок.

Из условия прочности определяют максимальное по модулю значение изгибающего момента:

. (3.12)

По значению с использованием эпюры , которая связывает с приложенными нагрузками, определяют максимально допустимые значения нагрузок.

Как отмечалось ранее, обычно касательные напряжения невелики и их вычисление не представляет практического интереса. Исключением из этого правила являются тонкостенные балки (например, сварные двутавровые), а также балки, нагруженные большим сосредоточенными силами вблизи опор, либо вообще имеющие малую длину. Для таких балок касательные напряжения могут иметь сравнительно большую величину, сопоставимую с величиной . В этих случаях, кроме расчета по нормальным напряжениям, проводят проверочный расчет по наибольшим касательным напряжениям, возникающим в том поперечном сечении, где поперечная сила максимальна. Это расчет обязательно выполняют и для балок из дерева, учитывая плохое сопротивление дерева сдвигу вдоль волокон.

Из формулы (3.5) следует, что наибольшие по модулю касательные напряжения будут возникать в точках, где отношение достигает максимума.

Условие прочности балки по касательным напряжениям будет иметь вид

.

(3.13)

Здесь –допускаемое напряжение материала балки на сдвиг.

Наибольшее значение берут из эпюры поперечных сил.

Из условия прочности (3.13) могут выполняться те же три вида расчетов, что и из условий прочности (3.6), (3.8) и (3.9).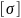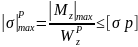
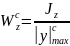